浙江省宁波市海曙区2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
1. 抛物线 的顶点坐标是( )A、 B、 C、 D、2. 在同一时刻,身高1.8米的小强在阳光下的影长为0.9米,一棵大树的影长为4.6米,则树的高度为( )A、9.8米 B、9.2米 C、8.2米 D、2.3米3. 如图,AB是⊙O的直径,MN是⊙O的切线,切点为N,如果∠MNB=52°,则∠NOA的度数为( )
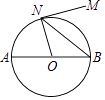 A、76° B、56° C、54° D、52°4. 下列事件中是必然事件的有( )A、抛掷一枚质地均匀的硬币,着地时正面向上 B、三角形内心到三边距离相等 C、测量宁波某天的最低气温,结果为 D、某个数的绝对值大于05. sin70°,cos70°,tan70°的大小关系是( )A、tan70°<cos70°<sin70° B、cos70°<tan70°<sin70° C、sin70°<cos70°<tan70° D、cos70°<sin70°<tan70°6. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是( )
A、76° B、56° C、54° D、52°4. 下列事件中是必然事件的有( )A、抛掷一枚质地均匀的硬币,着地时正面向上 B、三角形内心到三边距离相等 C、测量宁波某天的最低气温,结果为 D、某个数的绝对值大于05. sin70°,cos70°,tan70°的大小关系是( )A、tan70°<cos70°<sin70° B、cos70°<tan70°<sin70° C、sin70°<cos70°<tan70° D、cos70°<sin70°<tan70°6. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是( ) A、
A、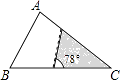 B、
B、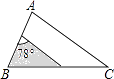 C、
C、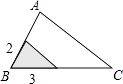 D、
D、 7. 已知 中, , , ,点P为边AB的中点,以点C为圆心,长度r为半径画圆,使得点A,P在⊙C内,点B在⊙C外,则半径r的取值范围是( )A、 B、 C、 D、8. 如图,在 中, , .以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的周长是( )
7. 已知 中, , , ,点P为边AB的中点,以点C为圆心,长度r为半径画圆,使得点A,P在⊙C内,点B在⊙C外,则半径r的取值范围是( )A、 B、 C、 D、8. 如图,在 中, , .以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的周长是( ) A、 B、 C、 D、9. 如图,在 中, , , ,P是AB边上一动点, 于点D,点E在P的右侧,且 ,连接CE,P从点A出发,沿AB方向运动,当E到达点B时,P停止运动,设 ,图中阴影部分面积 ,在整个运动过程中,函数值y随x的变化而变化的情况是( )
A、 B、 C、 D、9. 如图,在 中, , , ,P是AB边上一动点, 于点D,点E在P的右侧,且 ,连接CE,P从点A出发,沿AB方向运动,当E到达点B时,P停止运动,设 ,图中阴影部分面积 ,在整个运动过程中,函数值y随x的变化而变化的情况是( ) A、一直减小 B、一直增大 C、先减小后增大 D、先增大后减小10. 一个矩形按如图1的方式分割成三个直角三角形,把较大两个三角形纸片按图2中①、②两种方式放置,设①中的阴影部分面积为 ,②中的阴影部分面积为 ,当 时,则矩形的长短两边之比为( )
A、一直减小 B、一直增大 C、先减小后增大 D、先增大后减小10. 一个矩形按如图1的方式分割成三个直角三角形,把较大两个三角形纸片按图2中①、②两种方式放置,设①中的阴影部分面积为 ,②中的阴影部分面积为 ,当 时,则矩形的长短两边之比为( ) A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
11. 在 中, , , ,则 的值为.12. 小莉抛一枚质地均匀的硬币,连续抛三次,硬币落地均正面朝上,如果她第四次抛硬币,那么硬币正面朝上的概率为.13. 如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径OC=5cm,弦DE=8cm. 则直尺的宽为cm.
 14. 已知二次函数 中,函数y与自变量x的部分对应值如表:
14. 已知二次函数 中,函数y与自变量x的部分对应值如表:x
…
0
1
2
3
4
…
y
…
10
5
2
1
2
5
…
, 两点都在该函数的图象上,若 ,则m的值为.
15. 如图,在平面直角坐标系xOy中,半径为4的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线 与x轴、y轴分别交于点D、E,则 面积的最小值为. 16. 如图,正六边形ABCDEF中,G,H分别是边AF和DE上的点, , .则线段EH长.
16. 如图,正六边形ABCDEF中,G,H分别是边AF和DE上的点, , .则线段EH长.
三、解答题
-
17. 计算: .18. 在 的方格中, 的三个顶点都在格点上,我们把像这种顶点在格点的三角形叫格点三角形,请按要求完成下列作图
 (1)、在图1的方格中作出与 相似的最小格点三角形.(2)、在图2中把线段AC分成三条相等的线段 ,点E,F都在线段AC上.
(1)、在图1的方格中作出与 相似的最小格点三角形.(2)、在图2中把线段AC分成三条相等的线段 ,点E,F都在线段AC上.(①只能用无刻度的直尺作直线;②保留作图痕迹)
19. 在平面直角坐标系中,将抛物线 : 向左平移2个单位,向下平移3个单位得到新抛物线 . (1)、求新抛物线 的表达式;(2)、如图,将 沿x轴向左平移得到 ,点 的对应点 落在平移后的新抛物线 上,求点B与其对应点 的距离.20. 如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图,已知托板长 ,支撑板长 ,托板AB固定在支撑板顶端点C处,且 ,托板AB可绕点C转动,支撑板CD可绕点D转动.
(1)、求新抛物线 的表达式;(2)、如图,将 沿x轴向左平移得到 ,点 的对应点 落在平移后的新抛物线 上,求点B与其对应点 的距离.20. 如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图,已知托板长 ,支撑板长 ,托板AB固定在支撑板顶端点C处,且 ,托板AB可绕点C转动,支撑板CD可绕点D转动. (1)、若 , ,求点A到直线DE的距离;(2)、为了观看舒适,保持 ,在(1)的情况下,将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.21. 在抗击新冠疫情期间,某校数学兴趣小组调查了某天上午10分钟内进入校门口的累积人数变化情况,结果如下表:
(1)、若 , ,求点A到直线DE的距离;(2)、为了观看舒适,保持 ,在(1)的情况下,将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.21. 在抗击新冠疫情期间,某校数学兴趣小组调查了某天上午10分钟内进入校门口的累积人数变化情况,结果如下表:时间x(分钟)
0
2
4
6
8
10
累计人数y(人)
0
360
640
840
960
1000
(1)、请用适当的函数描述这10分钟内进入校门口人数的变化规律,写出y与x之间的函数解析式;(2)、如果学生一进入校门口后就开始排队测体温,若有6个测温组,每个测温组每分钟测温20人,设第x分钟时的排队人数为w,问第几分钟时等候测温排队总人数最多,最多有几人?22. 生活在数字时代的我们,很多场合用二维码(如图①)来表示不同的信息,类似地,可通过在网格中,对每一个小方格涂色或不涂色所得的图形来表示不同的信息,例如:网格中只有一个小方格(如图②),通过涂色或不涂色可表示两个不同的信息. (1)、用树状图或列表格的方法,求图③可表示不同信息的总个数(图中标号1、2表示两个不同位置的小方格,下同)(2)、图④为 的网格图,它可表示不同信息的总个数为;(3)、某校需要给每位师生制作一张“校园出入证”,准备在证件的右下角采用 的网格图来表示个人身份信息,若该校师生共506人,则n的最小值为.23. 已知 内接于⊙O, , 的平分线与⊙O交于点D,与AC交于点E,连接CD并延长与⊙O过点A的切线交于点F,记 .
(1)、用树状图或列表格的方法,求图③可表示不同信息的总个数(图中标号1、2表示两个不同位置的小方格,下同)(2)、图④为 的网格图,它可表示不同信息的总个数为;(3)、某校需要给每位师生制作一张“校园出入证”,准备在证件的右下角采用 的网格图来表示个人身份信息,若该校师生共506人,则n的最小值为.23. 已知 内接于⊙O, , 的平分线与⊙O交于点D,与AC交于点E,连接CD并延长与⊙O过点A的切线交于点F,记 . (1)、如图1,若 ,
(1)、如图1,若 ,①直接写出 的值为;
②当⊙O的半径为4时,直接写出图中阴影部分的面积为;
(2)、如图2,若 , , ,求DC的长.24. 定义:有一个内角等于与其相邻的两个内角之差的四边形称为幸福四边形.(1)、已知 , , ,请直接写出一个 的值 , 使四边形ABCD为幸福四边形;(2)、如图1, 中,D,E分别是边AB,AC上的点, .求证:四边形DBCE为幸福四边形; (3)、在(2)的条件下,如图2,过D,E,C三点作⊙O,与边AB交于另一点F,与边BC交于点G,且 .
(3)、在(2)的条件下,如图2,过D,E,C三点作⊙O,与边AB交于另一点F,与边BC交于点G,且 .①求证:EG是⊙O的直径;
②连结FG,若 , , ,求EG的长和幸福四边形DBCE的周长.

