浙江省杭州市上城区2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
1. 下列事件中,属于必然事件的是( )A、小明买彩票中奖 B、在—个只有红球的盒子里摸球,摸到了白球 C、任意抛掷一只纸杯,杯口朝下 D、任选三角形的两边,其差小于第三边2. 下列各式中正确的是( )A、 B、 C、 D、3. 已知圆内接四边形 中, ,则 ( )A、 B、 C、 D、4. 下列关于相似三角形的说法,正确的是( )A、等腰三角形都相似 B、直角三角形都相似 C、两边对应成比例,且其中一组对应角相等的两个三角形相似 D、一条直角边和斜边对应成比例的两个直角三角形相似5. 已知二次函数的图象过点 ,对称轴为直线 ,则这个函数图象必过点( )A、 B、 C、 D、6. 如图,在 中,作 ,分别交 于点 .若要使 与四边形 的面积相等,则 与 的比为( )
 A、 B、 C、 D、7. 下列函数图象经过变换后,过原点的是( )A、 向右平移3个单位 B、 向左平移3个单位 C、 向上平移1个单位 D、 关于x轴作轴对称变换8. 如图,点 均在以 为直径的 上,其中 ,则 ( )
A、 B、 C、 D、7. 下列函数图象经过变换后,过原点的是( )A、 向右平移3个单位 B、 向左平移3个单位 C、 向上平移1个单位 D、 关于x轴作轴对称变换8. 如图,点 均在以 为直径的 上,其中 ,则 ( )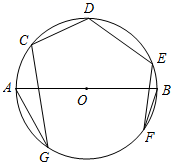 A、 B、 C、 D、9. 已知 和 是二次函数 (其中 是常数)上不同的两点,则判断m和n的大小关系正确的是( )A、 时, B、 时, C、 时, D、 时,10. 如图,四边形 内接于 ,对角线 于点E,若 的长与 的半径相等,则下列等式正确的是( )
A、 B、 C、 D、9. 已知 和 是二次函数 (其中 是常数)上不同的两点,则判断m和n的大小关系正确的是( )A、 时, B、 时, C、 时, D、 时,10. 如图,四边形 内接于 ,对角线 于点E,若 的长与 的半径相等,则下列等式正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图, 与 相交与点 ,则 .
 12. 某单位工会组织内部抽奖活动,共准备了100张奖券,设特等奖1名,一等奖10名,二等奖20个,三等奖30个,已知每张奖券获奖可能性相同,则抽一张奖券获得特等奖或一等奖的概率是.13. 已知 是抛物线 上的点,则将 按从小到大排列为.14. 如图,已知等边 以C为旋转中心,按逆时针方向旋转 ,得到 ,若 ,等边三角形边长为1,则点A的运动路径长为.
12. 某单位工会组织内部抽奖活动,共准备了100张奖券,设特等奖1名,一等奖10名,二等奖20个,三等奖30个,已知每张奖券获奖可能性相同,则抽一张奖券获得特等奖或一等奖的概率是.13. 已知 是抛物线 上的点,则将 按从小到大排列为.14. 如图,已知等边 以C为旋转中心,按逆时针方向旋转 ,得到 ,若 ,等边三角形边长为1,则点A的运动路径长为. 15. 已知在 中, ,则 .16. 如图,在等腰 中, 平分 ,点E在 的延长线上, 交 于点F,则图中与 相似的三角形为; 的长为.
15. 已知在 中, ,则 .16. 如图,在等腰 中, 平分 ,点E在 的延长线上, 交 于点F,则图中与 相似的三角形为; 的长为.
三、解答题
-
17. 已知半径为6的扇形面积为 ,求此扇形圆心角的角度.18. 已知有一个30度的角,两个45度的角,一个60度的角,(1)、从中任取两个角,请用树状图或列表求出两个角恰好互余的概率;(2)、已知在 中, 是上面四个角中的一个,求边 的长.19. 已知 中, .你能画一条直线把它分割成两个相似三角形吗?如果可以,请用尺规作出这条分割线,保留作图痕迹,并说明两个三角形相似的理由.
 20. 一位运动员推铅球,铅球经过的路线为如图所示的抛物线,
20. 一位运动员推铅球,铅球经过的路线为如图所示的抛物线, (1)、求铅球所经过路线的函数表达式;(2)、求出铅球的落地点离运动员有多远.21. 如图,在 中, ,以 为直径的 分别交 于点 ,连结 交 于点F.
(1)、求铅球所经过路线的函数表达式;(2)、求出铅球的落地点离运动员有多远.21. 如图,在 中, ,以 为直径的 分别交 于点 ,连结 交 于点F. (1)、求证:(2)、连结 ,交 于点G,若 ,且 ,求 的长.22. 已知二次函数 (其中 是常数)(1)、已知函数过点 ,求出b和c满足的关系式;(2)、若 ,求证:不论b为何值,该函数图象与x轴一定有交点;(3)、四位同学在研究此函数时,甲发现当 时, ;乙发现函数的最大值是9;丙发现函数图象的对称轴是 ;丁发现 是方程 的一个根.已知这四位同学中只有一位发现的结论是错误的,请直接写岀错误的那个同学是谁,并根据另三位同学的表述求出此函数表达式.23. 如图1, 是边长为2的等边三角形,以 为一边向下作矩形 ,其中 .M为线段 上的动点(且不与 重合),过M作矩形 ,使边 在线段 上.
(1)、求证:(2)、连结 ,交 于点G,若 ,且 ,求 的长.22. 已知二次函数 (其中 是常数)(1)、已知函数过点 ,求出b和c满足的关系式;(2)、若 ,求证:不论b为何值,该函数图象与x轴一定有交点;(3)、四位同学在研究此函数时,甲发现当 时, ;乙发现函数的最大值是9;丙发现函数图象的对称轴是 ;丁发现 是方程 的一个根.已知这四位同学中只有一位发现的结论是错误的,请直接写岀错误的那个同学是谁,并根据另三位同学的表述求出此函数表达式.23. 如图1, 是边长为2的等边三角形,以 为一边向下作矩形 ,其中 .M为线段 上的动点(且不与 重合),过M作矩形 ,使边 在线段 上. (1)、当 为 时,请直接写出矩形 的面积;(2)、设 ,矩形 的面积为y,
(1)、当 为 时,请直接写出矩形 的面积;(2)、设 ,矩形 的面积为y,①试求出y关于x的函数表达式;
②矩形 的面积y是否有最大值,若有,请求出这个最大值;若没有,请说明理由.
(3)、如图2,过点N作 的平行线,交线段 于点F,连结 ,若 为直角三角形,请直接写出线段 的长度.