广西壮族自治区来宾市2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
1. 下列函数中,属于反比例函数的是( )A、 B、 C、 D、2. 下列各组的四条线段 , , , 是成比例线段的是( )A、 , , , B、 , , , C、 , , , D、 , , ,3. 用配方法解方程: ,下列配方正确的是( )A、 B、 C、 D、4. 反比例函数y= (k≠0)的图象经过点(2,-4),若点(4,n)在反比例函数的图象上,则n等于( )A、﹣8 B、﹣4 C、﹣ D、﹣25. 如图,一个斜坡长130m,坡顶离水平地面的距离为50m,那么这个斜坡与水平地面夹角的正切值等于( )
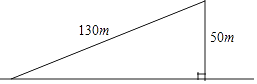 A、 B、 C、 D、6. 三角形两边的长是3和4,第三边的长是方程 的根,则该三角形的周长为( )A、10 B、12 C、14 D、12或147. 已知:如图,在 中, ,则下列等式成立的是( )
A、 B、 C、 D、6. 三角形两边的长是3和4,第三边的长是方程 的根,则该三角形的周长为( )A、10 B、12 C、14 D、12或147. 已知:如图,在 中, ,则下列等式成立的是( )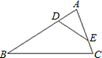 A、 B、 C、 D、8. 已知 , 是一元二次方程 的两个实数根且 ,则 的值为( ).A、0或1 B、0 C、1 D、9. 如图,在 中, , , .动点 , 分别从点 , 同时开始移动,点 的速度为 秒,点 的速度为 秒,点 移动到点 后停止,点 也随之停止运动.下列时间瞬间中,能使 的面积为 的是( )
A、 B、 C、 D、8. 已知 , 是一元二次方程 的两个实数根且 ,则 的值为( ).A、0或1 B、0 C、1 D、9. 如图,在 中, , , .动点 , 分别从点 , 同时开始移动,点 的速度为 秒,点 的速度为 秒,点 移动到点 后停止,点 也随之停止运动.下列时间瞬间中,能使 的面积为 的是( ) A、2秒钟 B、3秒钟 C、4秒钟 D、5秒钟10. 如图,一次函数 的图象与反比例函数 ( 为常数且 )的图象都经过 ,结合图象,则不等式 的解集是( )
A、2秒钟 B、3秒钟 C、4秒钟 D、5秒钟10. 如图,一次函数 的图象与反比例函数 ( 为常数且 )的图象都经过 ,结合图象,则不等式 的解集是( )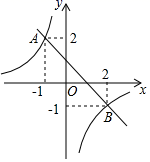 A、 B、 C、 或 D、 或11. 如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( )
A、 B、 C、 或 D、 或11. 如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( ) A、 B、 C、 D、12. 如图,在正方形 中, 是等边三角形, , 的延长线分别交 于点 , ,连接 , , 与 相交于点 .有下列结论:① ;② ;③ ;④ .其中正确的个数是( )
A、 B、 C、 D、12. 如图,在正方形 中, 是等边三角形, , 的延长线分别交 于点 , ,连接 , , 与 相交于点 .有下列结论:① ;② ;③ ;④ .其中正确的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 一元二次方程 的二次项系数、一次项系数及常数项之和为.14. 为了对1000件某品牌衬衣进行抽检,统计合格衬衣的件数,在相同条件下,经过大量的重复抽检,发现一件合格衬衣的频率稳定在常数0.98附近,由此可估计这1000件中不合格的衬衣约为件.15. △ABC中,已知 ,∠A、∠B为锐角,则∠C=°16. 如图,在一个长为40 m,宽为26m的矩形花园中修建小道(图中阴影部分),其中 ,每段小道的两边缘平行,剩余的地方种植花草,要使种植花草的面积为 ,那么 m.
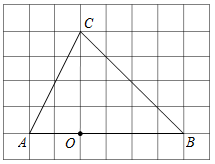
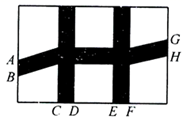 17. 如图,有一块三角形的土地,它的一条边 米, 边上的高 米,某单位要沿着边 修一座底面是矩形 的大楼,点 , 在边 上,点 , 分别在边 , 上,若大楼的宽是40米(即 米),则这个矩形的面积是平方米.
17. 如图,有一块三角形的土地,它的一条边 米, 边上的高 米,某单位要沿着边 修一座底面是矩形 的大楼,点 , 在边 上,点 , 分别在边 , 上,若大楼的宽是40米(即 米),则这个矩形的面积是平方米. 18. 如图,反比例函数 的图象经过矩形 对角线的交点 ,分别交 , 于点 、 .若四边形 的面积为12,则 的值为.
18. 如图,反比例函数 的图象经过矩形 对角线的交点 ,分别交 , 于点 、 .若四边形 的面积为12,则 的值为.
三、解答题
-
19. 解方程: .20. 如图,在 的网格图中,每个小正方形的边长均为1,点 和 的顶点均为小正方形的顶点.
 (1)、以 为位似中心,在网格图中作 ,使 和 位似,且位似比为 ;(2)、连接(1)中的 ,求四边形 的周长.(结果保留根号)21. 为了扎实推进精准扶贫工作,某地出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种4种和5种帮扶措施的贫困户分别称为 、 、 、 类贫困户,为检查帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
(1)、以 为位似中心,在网格图中作 ,使 和 位似,且位似比为 ;(2)、连接(1)中的 ,求四边形 的周长.(结果保留根号)21. 为了扎实推进精准扶贫工作,某地出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种4种和5种帮扶措施的贫困户分别称为 、 、 、 类贫困户,为检查帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:

请根据图中信息回答下面的问题:
(1)、本次抽样调查了户贫困户;(2)、本次共抽查了户 类贫困户,请补全条形统计图;(3)、若该地共有13000户贫困户,请估计至少得到4项帮扶措施的大约有多少户?22. 已知关于x的方程x2+ax+a﹣2=0.(1)、求证:不论a取何实数,该方程都有两个不相等的实数根;(2)、若该方程的一个根为1,求a的值及该方程的另一根.23. 如图,为测量一段笔直自西向东的河流的河面宽度,小明在南岸 处测得对岸 处一棵柳树位于北偏东 方向,他以每秒1.5米的速度沿着河岸向东步行40秒后到达 处,此时测得柳树位于北偏东 方向,试计算此段河面的宽度. 24. 如图,一次函数y=mx+5的图象与反比例函数y= (k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.
24. 如图,一次函数y=mx+5的图象与反比例函数y= (k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M. (1)、求一次函数和反比例函数的解析式;(2)、求△OAM的面积S;(3)、在y轴上求一点P,使PA+PB最小.
(1)、求一次函数和反比例函数的解析式;(2)、求△OAM的面积S;(3)、在y轴上求一点P,使PA+PB最小.
