广西壮族自治区百色市西林县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
1. 下列平面图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 经过不在同一直线上的三个点可以作圆的个数是( )A、1 B、2 C、3 D、无数3. 如图,Rt△ABC中,∠B=90°,AB=3,BC=2,则cosA=( )
2. 经过不在同一直线上的三个点可以作圆的个数是( )A、1 B、2 C、3 D、无数3. 如图,Rt△ABC中,∠B=90°,AB=3,BC=2,则cosA=( ) A、 B、 C、 D、4. 如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的 ,得到△COD,则CD的长度是( )
A、 B、 C、 D、4. 如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的 ,得到△COD,则CD的长度是( ) A、1 B、2 C、2 D、5. 抛物线 的顶点坐标是( )A、 B、 C、 D、6. 下列说法中,正确的是( )A、等弦所对的弧相等 B、在同圆或等圆中,相等的弧所对的弦相等 C、圆心角相等,所对的弦相等 D、弦相等所对的圆心角相等7. 如图, 与 轴交于点 , ,圆心 的横坐标为 ,则 的半径为( )
A、1 B、2 C、2 D、5. 抛物线 的顶点坐标是( )A、 B、 C、 D、6. 下列说法中,正确的是( )A、等弦所对的弧相等 B、在同圆或等圆中,相等的弧所对的弦相等 C、圆心角相等,所对的弦相等 D、弦相等所对的圆心角相等7. 如图, 与 轴交于点 , ,圆心 的横坐标为 ,则 的半径为( ) A、3 B、4 C、5 D、68. 已知反比例函数y= 的图象如图所示,则二次函数y=k2x2+x﹣2k的图象大致为( )
A、3 B、4 C、5 D、68. 已知反比例函数y= 的图象如图所示,则二次函数y=k2x2+x﹣2k的图象大致为( ) A、
A、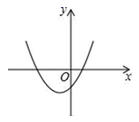 B、
B、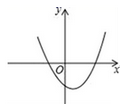 C、
C、 D、
D、 9. 如图,点A,B,C,D在⊙O上,AC是⊙O的直径,若∠CAD=25°,则∠ABD的度数为( )
9. 如图,点A,B,C,D在⊙O上,AC是⊙O的直径,若∠CAD=25°,则∠ABD的度数为( )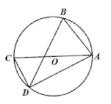 A、25° B、50° C、65° D、75°10. 在内接四边形 中, 只可能是下列四个选项中的( )A、 B、 C、 D、11. 在平面直角坐标系 中,将一块含有 角的直角三角板如图放置,直角顶点 的坐标为 ,顶点 的坐标 ,顶点 恰好落在第一象限的双曲线上,则该双曲线的解析式为( )
A、25° B、50° C、65° D、75°10. 在内接四边形 中, 只可能是下列四个选项中的( )A、 B、 C、 D、11. 在平面直角坐标系 中,将一块含有 角的直角三角板如图放置,直角顶点 的坐标为 ,顶点 的坐标 ,顶点 恰好落在第一象限的双曲线上,则该双曲线的解析式为( )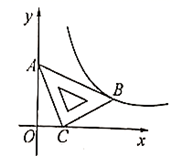 A、 B、 C、 D、12. 小翔在如图1所示的场地上匀速跑步,他从点A出发,沿箭头所示方向经过点B跑到点C,共用时30秒.他的教练选择了一个固定的位置观察小翔的跑步过程.设小翔跑步的时间为t(单位:秒),他与教练的距离为y(单位:米),表示y与t的函数关系的图象大致如图2所示,则这个固定位置可能是图1中的( )
A、 B、 C、 D、12. 小翔在如图1所示的场地上匀速跑步,他从点A出发,沿箭头所示方向经过点B跑到点C,共用时30秒.他的教练选择了一个固定的位置观察小翔的跑步过程.设小翔跑步的时间为t(单位:秒),他与教练的距离为y(单位:米),表示y与t的函数关系的图象大致如图2所示,则这个固定位置可能是图1中的( ) A、点M B、点N C、点P D、点Q
A、点M B、点N C、点P D、点Q二、填空题
-
13. 如果线段 , ,那么 和 的比例中项中 .14. 已知 ∽ ,且面积比为 ,若 的周长为 ,则 的周长是 .15. 如图,若关于 的二次函数 的图象与 轴交于两点,那么方程 的解是 .
 16. 如图是一斜坡的横截面,某人沿着斜坡从P处出发,走了13米到达M处,此时在铅垂方向上上升了5米,那么该斜坡的坡度是.
16. 如图是一斜坡的横截面,某人沿着斜坡从P处出发,走了13米到达M处,此时在铅垂方向上上升了5米,那么该斜坡的坡度是.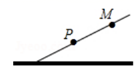 17. 一艘邮轮从港口 处出发,沿北偏东 方向行驶200海里到 港口,卸货后向正南方向行驶到 港口,此时 港口在邮轮的北偏西 方向上,这时邮轮与港口 相距海里.(保留根号)
17. 一艘邮轮从港口 处出发,沿北偏东 方向行驶200海里到 港口,卸货后向正南方向行驶到 港口,此时 港口在邮轮的北偏西 方向上,这时邮轮与港口 相距海里.(保留根号)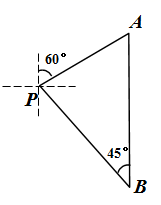 18. 如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若 是“好玩三角形”,且 ,则 .
18. 如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若 是“好玩三角形”,且 ,则 .三、解答题
-
19. 计算:20. 如图,在平面直角坐标系中,已知 的三个顶点的坐标分别为 , , .
 (1)、画出将 绕点 顺时针旋转 后所得到的图形 ;(2)、直接写出的点 , , 的坐标.21. 如图,已知反比例函数 的图象的一支位于第一象限.
(1)、画出将 绕点 顺时针旋转 后所得到的图形 ;(2)、直接写出的点 , , 的坐标.21. 如图,已知反比例函数 的图象的一支位于第一象限. (1)、求m的取值范围;(2)、O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.22. 如图,AB是圆O的一条弦,OD⊥AB,垂足为C,交圆O于点D,点E在圆O上.
(1)、求m的取值范围;(2)、O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.22. 如图,AB是圆O的一条弦,OD⊥AB,垂足为C,交圆O于点D,点E在圆O上. (1)、若∠AOD=50°,求∠DEB的度数;(2)、若OC=3,∠A=30°,求AB的长.23. 身高1.6米的张军同学在某一时刻测得自己的影长为1.4米,此刻她想测量学校旗杆的高度,但当她马上测量旗杆的影长时,发现因旗杆靠近一幢建筑物,影子一部分落在地面上,一部分落在墙上(如图),他先测得留在墙上的影子 米,又测地面部分的影长 米,你能根据上述数据帮张军同学测出旗杆的高度吗?
(1)、若∠AOD=50°,求∠DEB的度数;(2)、若OC=3,∠A=30°,求AB的长.23. 身高1.6米的张军同学在某一时刻测得自己的影长为1.4米,此刻她想测量学校旗杆的高度,但当她马上测量旗杆的影长时,发现因旗杆靠近一幢建筑物,影子一部分落在地面上,一部分落在墙上(如图),他先测得留在墙上的影子 米,又测地面部分的影长 米,你能根据上述数据帮张军同学测出旗杆的高度吗? 24. 某商店购进一批冬季保暖内衣,每套进价为100元,售价为130元,每星期可卖出80套.现因临近春节,商家决定降价促销,根据市场调查,每降价5元,每星期可多卖出20套.设保暖内衣售价为 元,每星期的销量为 件.(1)、求商家降价前每星期的销售利润为多少元?(2)、求 与 之间的函数关系式.(3)、当每件售价定为多少时,每星期的销售利润最大?最大销售利润是多少?
24. 某商店购进一批冬季保暖内衣,每套进价为100元,售价为130元,每星期可卖出80套.现因临近春节,商家决定降价促销,根据市场调查,每降价5元,每星期可多卖出20套.设保暖内衣售价为 元,每星期的销量为 件.(1)、求商家降价前每星期的销售利润为多少元?(2)、求 与 之间的函数关系式.(3)、当每件售价定为多少时,每星期的销售利润最大?最大销售利润是多少?

