辽宁省沈阳市铁西区、浑南区2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-03-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中，是一元二次方程的是（）

A、 $x^{2} = - 2$ B、 $x^{3} - 2 x + 1 = 0$ C、 $x^{2} + 3 x y + 1 = 0$ D、 $\frac{1}{x^{2}} + \frac{4}{x} - 5 = 0$

查看试题解析
2. 在一个不透明的袋子里装有红球，黄球共36个，这些球除颜色外都相同.小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数最有可能（）

A、5 B、9 C、15 D、24

查看试题解析
3. 由5个相同的小正方体组成的几何体如图所示，该几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 如图，在平面直角坐标系中，四边形OABC是矩形，点O是坐标原点，点A、C的坐标分别是 $(6 ， 0)$ ， $(0 ， 3)$ ，点B在第一象限，则点B的坐标是（）

A、 $(3 ， 6)$ B、 $(6 ， 3)$ C、 $(6 ， 6)$ D、 $(3 ， 3)$

查看试题解析
5. 函数 $y = - \frac{2}{x} (x > 0)$ 的图象位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 如图，在△ABC中，DE∥AB，且 $\frac{C D}{B D}$ ＝ $\frac{3}{2}$ ，则 $\frac{C E}{C A}$ 的值为（）

A、 $\frac{3}{5}$ B、 $\frac{2}{3}$ C、 $\frac{4}{5}$ D、 $\frac{3}{2}$

查看试题解析
7. 如图，把一块长为40cm，宽为30cm的矩形硬纸板的四角剪去四个相同小正方形，然后把纸板的四边沿虚线折起，并用胶带粘好，即可做成一个无盖纸盒.若该无盖纸盒的底面积为600cm² ，设剪去小正方形的边长为xcm，则可列方程为（）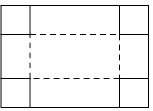

A、（30﹣2x）（40﹣x）＝600 B、（30﹣x）（40﹣x）＝600 C、（30﹣x）（40﹣2x）＝600 D、（30﹣2x）（40﹣2x）＝600

查看试题解析
8. 两个相似多边形的一组对应边分别是3cm和4.5cm，如果它们的周长之和是80cm，那么较大的多边形的周长是（）

A、16cm B、32cm C、48cm D、52cm

查看试题解析
9. 已知菱形的周长为8，两邻角的度数比为1：2，则菱形的面积为（）

A、8 $\sqrt{3}$ B、8 C、4 $\sqrt{3}$ D、2 $\sqrt{3}$

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 交x轴于点A，B，交 $y$ 轴于点C．若点A坐标为 $(- 4 ， 0)$ ，对称轴为直线 $x = - 1$ ，则下列结论错误的是（）

A、二次函数的最大值为 $a - b + c$ B、 $a + b + c > 0$ C、 $b^{2} - 4 a c > 0$ D、 $2 a + b = 0$

查看试题解析

二、填空题

11. 从 $\frac{1}{2}$ ， $- 1$ ，1，2中任取一个数作为a的值，使抛物线 $y = a x^{2} + b x + c$ （a，b，c是常数）的开口向上的概率为.

查看试题解析
12. 已知关于x的一元二次方程 $x^{2} + 5 x - m = 0$ 的一个根是2，则另一个根是.

查看试题解析
13. 若点 $A (- 5, a)$ ， $B (3, b)$ ， $C (6, c)$ 都在反比例函数 $y = \frac{4}{x}$ 的图象上，则a，b，c中最大的是.

查看试题解析
14. 如图，面积为16的菱形ABCD中，点O为对角线的交点，点E是边BC的中点，过点E作 $E F ⊥ B D$ 于点F， $E G ⊥ A C$ 于点G，则四边形EFOG的面积为.

查看试题解析
15. 竖直上抛物体时，物休离地而的高度 $h (m)$ 与运运动时间 $t (s)$ 之间的关系可以近似地用公式 $h = - 5 t^{2} + v_{0} t + h_{0}$ 表示，其中 $h_{0} (m)$ 是物体抛出时高地面的高度， $v_{0} (m / s)$ 是物体抛出时的速度.某人将一个小球从距地面 $1.5 m$ 的高处以 $20 m/s$ 的速度竖直向上抛出，小球达到的离地面的最大高度为m.

查看试题解析

三、解答题

16. 如图，菱形ABCD的对角线AC和BD交于点O，点G在射线OD上，且 $G D = 3 O D$ ，过点G作 $G E / / C D$ 交射线OC于点E，过点E作OE的垂线，与过点G作OG的垂线交于点P，得到矩形OEFG.射线AD交线段GF于点H，将 $△ G D H$ 沿直线AH折叠，得到 $△ M D H$ ，当点M在矩形OEFG的边上时， $\frac{B D}{A C} =$ .

查看试题解析
17. 若关于x的一元二次方程 $k x^{2} - 6 x + 9 = 0$ 有实数根，求k的取值范围.

查看试题解析
18. 如图，点D在 $∠ B A C$ 的内部， $∠ 1 = ∠ 2$ ， $∠ 1 + ∠ B A C = 180 °$ ， $B D = 1.5$ ， $C D = 2$ ，求AD的长.

查看试题解析
19. 在学校即将召开的运动会上，甲，乙两名学生准备从100米短跑（记为项目A），800米中长跑（记为项目B），跳远（记为项目C）三个项目中，分别随机选择一个项目参加比赛.请用画树状图或列表法求甲，乙两名学生选择相同项目的概率.

查看试题解析
20. 如图，正方形ABCD中，点P是对角线AC上一点，连接PB，边作 $P E ⊥ P B$ 交AD边于于点E，且点E不与点A，D重合，作 $P M ⊥ A D$ ， $P N ⊥ A B$ ，垂足分别为点M和N.

(1)、求证： $P M = P N$ ；

(2)、求证： $E M = B N$ .

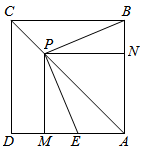查看试题解析
21. 某超市购进一种商品，进货单价为每件10元在销售过程中超市按相关规定.销售单价不低于1元且不高于19元如果该商品的销售单价x（单位：元/件）与日销售量y（单位：件）满足一次函数关系 $y = - 2 x + 40$ ，设该商品的日销售利润为w元，那么当该商品的销售单价x（元/件）定为多少时，日销售利润最大？最大利润是多少？

查看试题解析
22. 如图，一次函数 $y = k x + 1$ 的图象与反比例函数 $y = \frac{8}{x} (x > 0)$ 的图象交于点 $A (2 ， a)$ ，点B为x轴正半轴上一点，过B作x轴的垂线交反比例函数的图象于点C，交一次函数的图象于点D.

(1)、求a的值及一次函数 $y = k x + 1$ 的表达式；

(2)、若 $B D = 10$ ，求 $△ A C D$ 的面积.

查看试题解析
23. 如图，在平面直角坐标系中，直线 $y = k x$ 过点 $A (6 ， m)$ ，过点A作x轴的垂线，垂足为点B，过点A作y轴的垂线，垂足为点C. $∠ A O B = 60 °$ ， $C D ⊥ O A$ 于点D.动点P从点O出发，以每秒2个单位长度的速度向点A运动，动点Q从点A出发.以每秒 $\sqrt{3}$ 个单位长度的速度向点B运动.点P，Q同时开始运动，当点P到达点A时，点P，Q同时停止运动，设运动时间为 $t (s)$ ，且 $t > 0$ .

(1)、求m与k的值；

(2)、当点P运动到点D时，求t的值；

(3)、连接DQ，点E为DQ的中点，连接PE，当 $P E ⊥ D Q$ 时，请直接写出点P的坐标.

查看试题解析
24. 已知，在平行四边形 $A B C D$ 中， $∠ A B C = 45 °$ ， $A B = 3 \sqrt{2}$ ，点G是直线BC上一点，

(1)、如图，若 $A D = 6$ ，连接BD，AG，且 $A G ⊥ B D$ 于点E，
①求对角线BD的长；

②线段BG的长为；

(2)、连接AG，作 $B F ⊥ A G$ ，交直线AD于点F，当 $B F = \frac{8}{3} A G$ 时，请直接写出线段BG的长.

查看试题解析
25. 在平面直角坐标系中，抛物线 $y = x^{2} - k x - 2 k$ （k为常数）的顶点为N.

(1)、如图，若此抛物线过点 $A (3 ， - 1)$ ，求抛物线的函数表达式；

(2)、在（1）的条件下，抛物线与y轴交于点B，
①求 $∠ A B O$ 的度数；

②连接AB，点P为线段AB上不与点A，B重合的一个动点，过点P作 $C D / / x$ 轴交抛物线在第四象限部分于点C，交y轴于点D，连接PN，当 $△ B P N \sim △ B N A$ 时，线段CD的长为.

(3)、无论k取何值，抛物线都过定点H，点M的坐标为 $(2 ， 0)$ ，当 $∠ M H N = 90 °$ 时，请直接写出k的值.

查看试题解析