宁夏回族自治区吴忠市盐池县2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-03-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件是必然事件的是（）

A、打开电视机，正在播放篮球比赛 B、守株待兔 C、明天是晴天 D、在只装有5个红球的袋中摸出1球，是红球.

查看试题解析
3. 方程2x（x﹣3）=5（x﹣3）的根是（）

A、x= $\frac{5}{2}$ B、x=3 C、x₁= $\frac{5}{2}$ ，x₂=3 D、x₁=﹣ $\frac{5}{2}$ ，x₂=3

查看试题解析
4. 电影《流浪地球》一上映就获得追捧，第一天票房收入约8亿元，第三天票房收入达到了11.52亿元，设第一天到第三天票房收入平均每天增长的百分率为x，则可列方程（　　）

A、8（1+x）＝11.52 B、8（1+2x）＝11.52 C、8（1+x） $^{2}$ ＝11.52 D、8（1﹣x） $^{2}$ ＝11.52

查看试题解析
5. 如图，抛物线 $y_{1} = - x^{2} + 4 x$ 和直线 $y_{2} = 2 x$ ，当 $y_{1} < y_{2}$ 时，x的取值范围是（）

A、 $0 < x < 2$ B、 $x < 0$ 或 $x > 2$ C、 $x < 0$ 或 $x > 4$ D、 $0 < x < 4$

查看试题解析
6. 如图，⊙O是△ABC的外接圆，已知∠ACB＝60°，则∠ABO的大小为（）

A、30° B、40° C、45° D、50°

查看试题解析
7. 如图为二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象，则下列说法：① $a > 0$ ；② $2 a + b = 0$ ；③ $a + b + c > 0$ ；④ $△ > 0$ ；⑤ $4 a - 2 b + c < 0$ ，其中正确的个数为（）

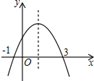A、1 B、2 C、3 D、4

查看试题解析
8. ⊙O的半径是13，弦AB $∥$ CD ， AB＝24，CD＝10，则AB与CD的距离是（　　）

A、7 B、17 C、7或17 D、34

查看试题解析

二、填空题

9. 将抛物线： $y = x^{2} - 2 x$ 向下平移3个单位，再向右平移4个单位得到的抛物线是.

查看试题解析
10. 一个圆锥的侧面展开图是半径为8cm、圆心角为120°的扇形，则此圆锥底面圆的半径为．

查看试题解析
11. 若函数y＝(a－1)x²－4x＋2a的图象与x轴有且只有一个交点，则a的值为．

查看试题解析
12. 用一条长40cm的绳子围成一个面积为64cm²的矩形.设矩形的一边长为 cm，则可列方程为.

查看试题解析
13. 如图，在Rt△ABC中，∠C＝90°，CA＝CB＝2.分别以A、B、C为圆心，以 $\frac{1}{2}$ AC为半径画弧，三条弧与边AB所围成的阴影部分的面积是.（保留π）

查看试题解析
14. 如图表示一圆柱形输水管的横截面，阴影部分为有水部分，如果水的最大深度CD为2m，水面宽AB为8m，则输水管的半径为m.

查看试题解析
15. 将含有 30°角的直角三角板 OAB 如图放置在平面直角坐标系中，OB 在 x轴上，若 OA＝2，将三角板绕原点 O 顺时针旋转 75°，则点 A 的对应点 A′ 的坐标为．

查看试题解析
16. 如图，正方形ABCD内接与⊙0，AB= $2 \sqrt{2}$ ，则弧AB的长是.

查看试题解析

三、解答题

17. 解方程

(1)、 $(x + 3) (x - 1) = 5$

(2)、 $x (x + 3) = x + 3$

查看试题解析
18. 已知：关于x的方程x²+kx﹣2＝0

(1)、求证：方程有两个不相等的实数根；

(2)、若方程的一个根是﹣1，求另一个根及k值．

查看试题解析
19. 如图，在平面直角坐标系中，A（0，1），B（﹣3，5），C（﹣3，1）.

（ 1 ）在图中画出△ABC以A为旋转中心，沿顺时针方向旋转90^o后的图形△AB₁C₁ ，并写出B₁、C₁两点的坐标；

（ 2 ）在图中画出与△ABC关于原点对称的图形△A₂B₂C₂ ，并写出B₂、C₂两点的坐标.

查看试题解析

20. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共10只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复.下表是活动进行中的一组统计数据：

摸球的次数	100	150	200	500	800	1000
摸到白球的次数	58	96	116	295	484	601
摸到白球的频率	0.58	0.64	0.58	0.59	0.605	0.601

(1)、请估计：当n很大时，摸到白球的频率将会接近；（保留二个有效数字）

(2)、试估算口袋中黑、白两种颜色的球各有多少只？

(3)、请画树状图或列表计算：从中一次摸两只球，这两只球颜色不同的概率是多少？

查看试题解析

21. 已知二次函数 $y = - x^{2} + b x + c$ 的图象如图所示，解决下列问题：

(1)、关于 $x$ 的一元二次方程 $- x^{2} + b x + c = 0$ 的解为；

(2)、求此抛物线的解析式；

(3)、当 $x$ 为值时， $y < 0$ ；

(4)、若直线 $y = k$ 与抛物线没有交点，直接写出 $k$ 的范围.

查看试题解析
22. 小区要用篱笆围成一个四边形花坛、花坛的一边利用足够长的墙，另三边所用的篱笆之和恰好为18米.围成的花坛是如图所示的四边形ABCD，其中∠ABC=∠BCD=90°，且BC=2AB.设AB边的长为x米.四边形ABCD面积为S平方米.

(1)、请直接写出S与x之间的函数关系式（不要求写出自变量x的取值范围）.

(2)、当x是多少时，四边形ABCD面积S最大？最大面积是多少？

查看试题解析
23. 如图，点D是等边△ABC中BC边的延长线上一点，且AC＝CD，以AB为直径作⊙O，分别交边AC、BC于点E、点F.

(1)、求证：AD是⊙O的切线；

(2)、连接OC，交⊙O于点G，若AB＝8，求线段CE、CG与 $\overset{⌢}{G E}$ 围成的阴影部分的面积S.

查看试题解析
24. 某文具店购进一批纪念册，每本进价为20元，出于营销考虑，要求每本纪念册的售价不低于20元且不高于28元，在销售过程中发现该纪念册每周的销售量y（本）与每本纪念册的售价x（元）之间满足一次函数关系：当销售单价为22元时，销售量为36本；当销售单价为24元时，销售量为32本．

(1)、求出y与x的函数关系式；

(2)、当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是多少元？

(3)、设该文具店每周销售这种纪念册所获得的利润为w元，将该纪念册销售单价定为多少元时，才能使文具店销售该纪念册所获利润最大？最大利润是多少？

查看试题解析
25. 已知抛物线y＝ax²＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．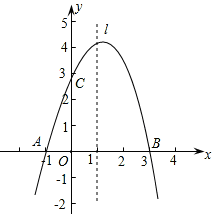

(1)、求抛物线的函数关系式；

(2)、设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；

(3)、在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．

查看试题解析