辽宁省沈阳市法库县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
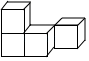
1. 如图是由4个大小相同的小正方体摆成的几何体,它的左视图是( )
 A、
A、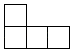 B、
B、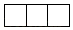 C、
C、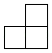 D、
D、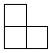 2. 下列函数中y是x的反比例函数的是( )A、y= B、xy=8 C、y= D、y=3. 平行四边形、矩形、菱形、正方形共有的性质是( ).A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、对角线互相垂直平分4. 从甲、乙、丙、丁四人中抽调一人参加“抗疫”志愿者服务队,恰好抽到丙的概率是( )A、 B、 C、 D、5. 一元二次方程 根的情况是( )A、有两个相等的实数根 B、无实数根 C、有两个不相等的实数根 D、无法确定6. 在 中, ,若 ,则 的值为( )A、 B、 C、 D、7. 下列对二次函数 的图象的描述,正确的是( )A、开口向下 B、对称轴是 轴 C、经过原点 D、在对称轴右侧 随 的增大而减小8. 如图,线段CD两个端点的坐标分别为C(4,4)、D(6,2),以原点O为位似中心,在第一象限内将线段CD缩小为线段AB,若点B的坐标为(3,1),则点A的坐标为( )
2. 下列函数中y是x的反比例函数的是( )A、y= B、xy=8 C、y= D、y=3. 平行四边形、矩形、菱形、正方形共有的性质是( ).A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、对角线互相垂直平分4. 从甲、乙、丙、丁四人中抽调一人参加“抗疫”志愿者服务队,恰好抽到丙的概率是( )A、 B、 C、 D、5. 一元二次方程 根的情况是( )A、有两个相等的实数根 B、无实数根 C、有两个不相等的实数根 D、无法确定6. 在 中, ,若 ,则 的值为( )A、 B、 C、 D、7. 下列对二次函数 的图象的描述,正确的是( )A、开口向下 B、对称轴是 轴 C、经过原点 D、在对称轴右侧 随 的增大而减小8. 如图,线段CD两个端点的坐标分别为C(4,4)、D(6,2),以原点O为位似中心,在第一象限内将线段CD缩小为线段AB,若点B的坐标为(3,1),则点A的坐标为( )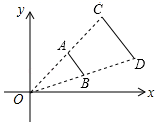 A、(0,3) B、(1,2) C、(2,2) D、(2,1)9. 如图,A,B是反比例函数y= 图象上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD= OC,S四边形ABCD=9,则k值为( )
A、(0,3) B、(1,2) C、(2,2) D、(2,1)9. 如图,A,B是反比例函数y= 图象上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD= OC,S四边形ABCD=9,则k值为( )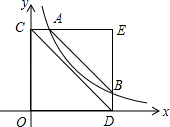 A、8 B、10 C、12 D、16.10. 抛物线y=ax2+bx+c(a≠0)如图所示,下列结论:①b2﹣4ac>0;②a+b+c=2;③abc<0;④a﹣b+c<0,其中正确的有( )
A、8 B、10 C、12 D、16.10. 抛物线y=ax2+bx+c(a≠0)如图所示,下列结论:①b2﹣4ac>0;②a+b+c=2;③abc<0;④a﹣b+c<0,其中正确的有( )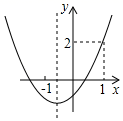 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
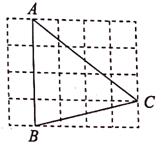
11. 方程x2﹣2x=0的解为 .12. 抛物线y=x2+2x+3的顶点坐标是.13. 如图,在 的正方形网格中,每个小正方形的边长都是1, 的顶点都在这些小正方形的顶点上,则 的值为 .
 14.
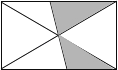
14.小明把如图所示的矩形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是 .
 15. 如图,小明与大树之间放置了一面平面镜,平面镜到小明的距离是2米、到大树的距离是6米时,小明恰好能从平面镜中看见大树的树尖,若小明的眼睛距离地面1.5米,则大树的高为米.
15. 如图,小明与大树之间放置了一面平面镜,平面镜到小明的距离是2米、到大树的距离是6米时,小明恰好能从平面镜中看见大树的树尖,若小明的眼睛距离地面1.5米,则大树的高为米.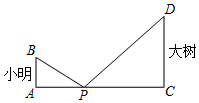 16. 在△ABC中,CO是AB边上的中线,∠AOC=60°,AB=2,点P是直线OC上的一个动点,则当△PAB为直角三角形时,边AP的长为.
16. 在△ABC中,CO是AB边上的中线,∠AOC=60°,AB=2,点P是直线OC上的一个动点,则当△PAB为直角三角形时,边AP的长为.三、解答题
-
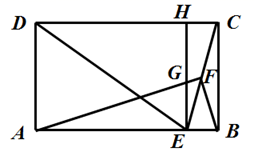
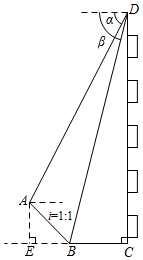
17.18. 在一个不透明袋子中装有1个红球,1个绿球和n个白球,这些球除颜色外均相同.(1)、从袋中随机摸出一个球,记录其颜色后放回,搅匀后再随机摸出一个球,经过大量重复该实验,发现摸到绿球的频率值稳定于 ,则n的值是;(2)、当n=2时,从该不透明的袋子中一次摸出两个球,求摸出的两个球颜色不同的概率.(用“画树状图”或“列表”的方法写出分析过程)19. 如图,某建筑物CD高96米,它的前面有一座小山,其斜坡AB的坡度为 .为了测量山顶A的高度,在建筑物顶端D处测得山顶A和坡底B的俯角分别为α、β.已知 , ,求山顶A的高度AE(C、B、E在同一水平面上).
 20. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.过点C作CF//BD交OE的延长线于点F,连接DF.
20. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.过点C作CF//BD交OE的延长线于点F,连接DF.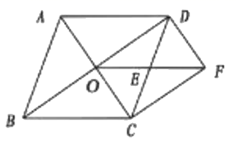
求证:
(1)、△ODE≌△FCE;(2)、四边形OCFD是矩形。21. 2020年突如其来的新型冠状病毒疫情,给生鲜电商带来了意想不到的流量和机遇,据统计某生鲜电商平台1月份的销售额是1440万元,3月份的销售额是2250万元.(1)、若该平台1月份到3月份的月平均增长率都相同,求月平均增长率是多少?(2)、市场调查发现,某水果在“盒马鲜生”平台上的售价为20元/千克时,每天能销售200千克,售价每降价2元,每天可多售出100千克,为了推广宣传,商家决定降价促销,同时尽量减少库存,已知该水果的成本价为12元/千克,若使销售该水果每天获利1750元,则售价应降低多少元?22. 如图,在平行四边形 中, 是 的延长线上一点, 与 交于点 .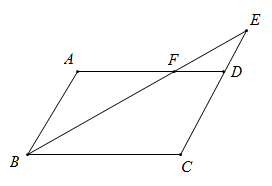 (1)、求证:(2)、若 的面积为 ,求平行四边形 的面积23.
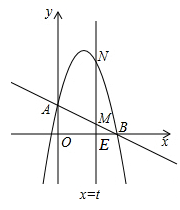
(1)、求证:(2)、若 的面积为 ,求平行四边形 的面积23.如图,已知一次函数y= x﹣3与反比例函数 的图象相交于点A(4,n),与 轴相交于点B.
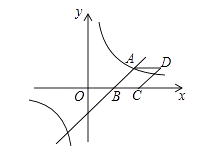 (1)、填空:n的值为 , k的值为;(2)、以AB为边作菱形ABCD,使点C在 轴正半轴上,点D在第一象限,求点D的坐标;(3)、考察反比函数 的图象,当 时,请直接写出自变量 的取值范围.
(1)、填空:n的值为 , k的值为;(2)、以AB为边作菱形ABCD,使点C在 轴正半轴上,点D在第一象限,求点D的坐标;(3)、考察反比函数 的图象,当 时,请直接写出自变量 的取值范围.