辽宁省锦州市2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
1. 如图所示物体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 在一个不透明的口袋中,装有若干个红球和6个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的频率是0.3,则估计口袋中红球约有( )A、12个 B、14个 C、18个 D、20个3. 已知 , , ,则 与 的面积之比为( )A、 B、 C、 D、4. 关于 的一元二次方程 有两个实数根,则实数 的取值范围是( )A、 B、 C、 D、5. 下列说法正确的是( )A、矩形的对角线互相垂直 B、菱形的对角线相等 C、正方形的对角线互相垂直且相等 D、平行四边形的对角线相等6. 如图,小明(用 表示)站在旗杆(用 表示)的前方 处,某一时刻小明在地面上的影子 恰好与旗杆在地面上的影子 重合,若 , ,则旗杆 的高度为( )
2. 在一个不透明的口袋中,装有若干个红球和6个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的频率是0.3,则估计口袋中红球约有( )A、12个 B、14个 C、18个 D、20个3. 已知 , , ,则 与 的面积之比为( )A、 B、 C、 D、4. 关于 的一元二次方程 有两个实数根,则实数 的取值范围是( )A、 B、 C、 D、5. 下列说法正确的是( )A、矩形的对角线互相垂直 B、菱形的对角线相等 C、正方形的对角线互相垂直且相等 D、平行四边形的对角线相等6. 如图,小明(用 表示)站在旗杆(用 表示)的前方 处,某一时刻小明在地面上的影子 恰好与旗杆在地面上的影子 重合,若 , ,则旗杆 的高度为( ) A、 B、 C、 D、7. 如图,在 中, , ,按以下步骤作图:①以点 为圆心,以 长为半径作弧,交 于点 ;②分别以点 , 为圆心,以 长为半径作弧,两弧相交于点 ,作射线 交 于点 ,则 的长为( )
A、 B、 C、 D、7. 如图,在 中, , ,按以下步骤作图:①以点 为圆心,以 长为半径作弧,交 于点 ;②分别以点 , 为圆心,以 长为半径作弧,两弧相交于点 ,作射线 交 于点 ,则 的长为( )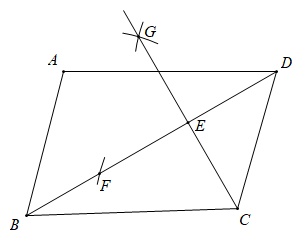 A、3 B、 C、4 D、8. 如图,正方形 的对角线 , 交于点 , 是 上的一点,连接 ,过点 作 于点 ,交 于点 , 交 于点 ,若正方形 的边长为4,下列结论:① ;② ;③当 为 中点时, ;④ ,其中正确的是( )
A、3 B、 C、4 D、8. 如图,正方形 的对角线 , 交于点 , 是 上的一点,连接 ,过点 作 于点 ,交 于点 , 交 于点 ,若正方形 的边长为4,下列结论:① ;② ;③当 为 中点时, ;④ ,其中正确的是( ) A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
9. 已知关于 的一元二次方程 有一个根是 ,则 的值为.10. 某批足球的质量检验结果如下:
抽取的足球数n
100
200
400
600
800
1000
1200
优等品频数m
93
192
380
561
752
941
1128
优等品频率
0.930
0.960
0.950
0.935
0.940
0.941
0.940
从这批足球中,任意抽取的一只足球是优等品的概率的估计值是.
11. 如图,小军、小珠之间的距离为 ,他们在同一盏路灯下的影长分别为 , ,已知小军、小珠的身高分别为 , ,则路灯的高为 . 12. 若点 和点 在反比例函数 的图象上,则 与 的大小关系为.13. 2021年元旦联欢会上,某班同学之间互赠新年贺卡,共赠贺卡190张,设全班有 名同学则可列方程为.14. 如图,在 中, , ,以 为边作正方形 ,连接 ,则 .
12. 若点 和点 在反比例函数 的图象上,则 与 的大小关系为.13. 2021年元旦联欢会上,某班同学之间互赠新年贺卡,共赠贺卡190张,设全班有 名同学则可列方程为.14. 如图,在 中, , ,以 为边作正方形 ,连接 ,则 . 15. 如图,在矩形 中,对角线 , 交于点 ,过点 作 ,交 的延长线于点 ,若 , ,则 的长为.
15. 如图,在矩形 中,对角线 , 交于点 ,过点 作 ,交 的延长线于点 ,若 , ,则 的长为. 16. 如图,在菱形 中, , , , 分别是边 , 上的动点,连接 , , , 分别为 , 的中点,连接 ,则 的最小值为.
16. 如图,在菱形 中, , , , 分别是边 , 上的动点,连接 , , , 分别为 , 的中点,连接 ,则 的最小值为.
三、解答题
-
17. 用适当的方法解下列一元二次方程:(1)、 ;(2)、 .18. 如图,在平面直角坐标系中, 的顶点 的坐标为 ,顶点 , 都在小正方形的格点上
 (1)、点 的坐标为 , 点 的坐标为;(2)、以原点 为位似中心,在所给的网格中画出一个 ,使得 与 位似,且相似比为 .19. 小明和小刚打算寒假去北京游玩,他们准备从锦州南站乘坐动车去北京,锦州南站每天开四个检票口,其中有三个电子检票口,分别记为 , , ,一个人工检票口记为 (如图).
(1)、点 的坐标为 , 点 的坐标为;(2)、以原点 为位似中心,在所给的网格中画出一个 ,使得 与 位似,且相似比为 .19. 小明和小刚打算寒假去北京游玩,他们准备从锦州南站乘坐动车去北京,锦州南站每天开四个检票口,其中有三个电子检票口,分别记为 , , ,一个人工检票口记为 (如图). (1)、小明随机选择一个检票口进入候车大厅,那么他从电子检票口 进入的概率为;(2)、若小明和小刚分别随机选择其中一个检票口进入候车大厅,请用树状图或列表法求他们选择不同电子检票口的概率.20. 如图,在矩形 中, , .动点 从点 出发以 的速度沿 向点 运动,动点 从点 出发以 的速度沿 向点 运动,设运动时间为 .
(1)、小明随机选择一个检票口进入候车大厅,那么他从电子检票口 进入的概率为;(2)、若小明和小刚分别随机选择其中一个检票口进入候车大厅,请用树状图或列表法求他们选择不同电子检票口的概率.20. 如图,在矩形 中, , .动点 从点 出发以 的速度沿 向点 运动,动点 从点 出发以 的速度沿 向点 运动,设运动时间为 . (1)、当 时,求 的值;(2)、当 时,求 的值.21. 某小家电经销商销售一种成本为每个50元的台灯.当每个台灯的售价定为80元时,每周可卖出600个,为了尽可能让利于顾客,经销商决定降价销售.经市场调查发现,这种台灯每周的销量每增加100个,该台灯的售价相应降低2元.如果该经销商每周要获得利润22000元,那么这种台灯的售价应为多少元?22. 如图,点 , 在 轴上,以 为边的正方形 在 轴上方,点 的坐标为 ,反比例函数 的图象经过 的中点 , 是 上的一个动点,将 沿 所在直线折叠得到 .
(1)、当 时,求 的值;(2)、当 时,求 的值.21. 某小家电经销商销售一种成本为每个50元的台灯.当每个台灯的售价定为80元时,每周可卖出600个,为了尽可能让利于顾客,经销商决定降价销售.经市场调查发现,这种台灯每周的销量每增加100个,该台灯的售价相应降低2元.如果该经销商每周要获得利润22000元,那么这种台灯的售价应为多少元?22. 如图,点 , 在 轴上,以 为边的正方形 在 轴上方,点 的坐标为 ,反比例函数 的图象经过 的中点 , 是 上的一个动点,将 沿 所在直线折叠得到 . (1)、求反比例函数 的表达式;(2)、若点 落在 轴上,求线段 的长及点 的坐标.
(1)、求反比例函数 的表达式;(2)、若点 落在 轴上,求线段 的长及点 的坐标.


