辽宁省本溪市2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 主视图、俯视图和左视图分别是下列图形的物体是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列计算的结果是x5的为( )A、x10÷x2 B、x6﹣x C、x2•x3 D、(x2)34. 下列说法正确的是( )A、为保证“嫦娥五号”成功发射,对其零部件检查采取抽样方式 B、“守株待兔”是必然事件 C、有5个数都是6的整数倍,从中任选2个数都是偶数的概率是1 D、某彩票中心宣布,某期彩票的中奖率是70%,小明买了10张彩票,一定有7张中奖5. 菱形和矩形一定都具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、每条对角线平分一组对角6. 下列四个图形中,轴对称图形的个数是( )
3. 下列计算的结果是x5的为( )A、x10÷x2 B、x6﹣x C、x2•x3 D、(x2)34. 下列说法正确的是( )A、为保证“嫦娥五号”成功发射,对其零部件检查采取抽样方式 B、“守株待兔”是必然事件 C、有5个数都是6的整数倍,从中任选2个数都是偶数的概率是1 D、某彩票中心宣布,某期彩票的中奖率是70%,小明买了10张彩票,一定有7张中奖5. 菱形和矩形一定都具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、每条对角线平分一组对角6. 下列四个图形中,轴对称图形的个数是( ) A、1 B、2 C、3 D、47. 某商品经过连续两次涨价,销售单价由原来162元涨到200元,设平均每次涨价的百分比为x,根据题意可列方程为( )A、 B、 C、 D、8. 如图,在菱形ABCD中, , ,则 的周长等于( )
A、1 B、2 C、3 D、47. 某商品经过连续两次涨价,销售单价由原来162元涨到200元,设平均每次涨价的百分比为x,根据题意可列方程为( )A、 B、 C、 D、8. 如图,在菱形ABCD中, , ,则 的周长等于( )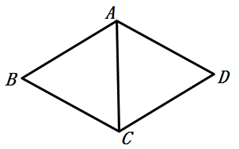 A、20 B、15 C、10 D、129. 在同一直角坐标系中,函数y=mx+m和函数y=mx2+2x+2(m是常数,且m≠0)的图象可能是( )A、
A、20 B、15 C、10 D、129. 在同一直角坐标系中,函数y=mx+m和函数y=mx2+2x+2(m是常数,且m≠0)的图象可能是( )A、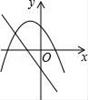 B、
B、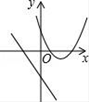 C、
C、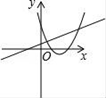 D、
D、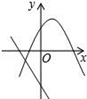 10. 如图,边长为2的正方形ABCD中,点P从点A出发沿路线 匀速运动至点D停止,已知点P的速度为1,运动时间为t,以P.A.B为顶点的三角形面积为S,则S与t之间的函数图象可能是( )
10. 如图,边长为2的正方形ABCD中,点P从点A出发沿路线 匀速运动至点D停止,已知点P的速度为1,运动时间为t,以P.A.B为顶点的三角形面积为S,则S与t之间的函数图象可能是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 因式分解: .12. 在平面直角坐标系中,点 关于 轴对称的点的坐标是 .13. 不等式组 的整数解是.14. 已知一个直角三角形的两边长分别为3和4,则斜边上的高是.15. 某校射击队从甲、乙、丙、丁四人中选拔一人参加射击比赛,在选拔赛中每人射击10次,计算他们10发成绩的平均数(环)及方差如下表.
甲
乙
丙
丁
平均数
8.2
8.0
8.2
8.0
方差
2.0
1.8
1.5
1.6
请你根据表中数据选择其中一人参加比赛,最合适的人选是.
16. 已知关于 的一元二次方程 有实数根,则 的取值范围是.17. 如图,在平面直角坐标系中,点 在直线 与直线 之间(不在两条直线上),则a的取值范围是. 18. 如图, 中, , .以OB为直角边向外作等腰直角三角形 ,以 为直角边向外作等腰直角三角形 ,以 为直角边向外作等腰直角三角形 ,连接 , , …分别与OB, , …交于点 , , ,…,按此规律继续下去,形成若干个阴影三角形,若 为第1个阴影三角形, 为第2个阴影三角形,则第2020个阴影三角形的面积为.
18. 如图, 中, , .以OB为直角边向外作等腰直角三角形 ,以 为直角边向外作等腰直角三角形 ,以 为直角边向外作等腰直角三角形 ,连接 , , …分别与OB, , …交于点 , , ,…,按此规律继续下去,形成若干个阴影三角形,若 为第1个阴影三角形, 为第2个阴影三角形,则第2020个阴影三角形的面积为.
三、解答题
-
19. 先化简,再求值: ,其中 .20. 给你一个锐角三形ABC和任意一条直线MN问题:请同学们利用直线MN.
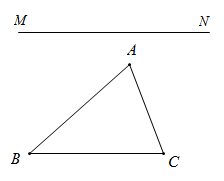 (1)、在 边上或边的延长线作出一个三角形与 相似,并请说明理由;(2)、这样的三角形还能做出几种?利用作图(不保留作图痕迹)简单说明,不必说明理由.21. 为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
(1)、在 边上或边的延长线作出一个三角形与 相似,并请说明理由;(2)、这样的三角形还能做出几种?利用作图(不保留作图痕迹)简单说明,不必说明理由.21. 为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题: (1)、此次共调查了名学生;扇形统计图中D所在扇形的圆心角为;(2)、将上面的条形统计图补充完整;(3)、若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的人数;(4)、现有“非常了解”的2名男生,2名女生,从这4名学生中随机抽取2名学生进行座谈,刚好抽到同性别学生的概率是多少?22. 如图,已知反比例函数 与一次函数 的图象在第一象限相交于点 .
(1)、此次共调查了名学生;扇形统计图中D所在扇形的圆心角为;(2)、将上面的条形统计图补充完整;(3)、若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的人数;(4)、现有“非常了解”的2名男生,2名女生,从这4名学生中随机抽取2名学生进行座谈,刚好抽到同性别学生的概率是多少?22. 如图,已知反比例函数 与一次函数 的图象在第一象限相交于点 .
 (1)、试确定这两个函数的表达式;(2)、求出这两个函数图象的另一个交点 的坐标,并根据图象写出使反比例函数的值大于一次函数的值的 取值范围.23. 如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一知输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏东49°方向,B位于南偏西41°方向.
(1)、试确定这两个函数的表达式;(2)、求出这两个函数图象的另一个交点 的坐标,并根据图象写出使反比例函数的值大于一次函数的值的 取值范围.23. 如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一知输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏东49°方向,B位于南偏西41°方向. (1)、线段BQ与PQ是否相等?请说明理由;(2)、求A,B间的距离.(参考数据cos41°=0.75)24. 某商品在商场的售价为每件60元,每星期可卖出300件,甲、乙两位网红主播在直播间为商场售货.甲主播每件商品每涨价1元,每星期少卖出10件;改为乙时,每降价1元,每星期可多卖出18件.已知商品的进价为每件40元,通过计算你认为甲、乙每星期谁能使利润最大?
(1)、线段BQ与PQ是否相等?请说明理由;(2)、求A,B间的距离.(参考数据cos41°=0.75)24. 某商品在商场的售价为每件60元,每星期可卖出300件,甲、乙两位网红主播在直播间为商场售货.甲主播每件商品每涨价1元,每星期少卖出10件;改为乙时,每降价1元,每星期可多卖出18件.已知商品的进价为每件40元,通过计算你认为甲、乙每星期谁能使利润最大?

