甘肃省定西市安定区2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-03-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列成语所描述的事件为随机事件的是（）

A、守株待兔 B、水中捞月 C、瓮中捉鳖 D、拔苗助长

查看试题解析
3. 已知x=2是一元二次方程x²+mx+4=0的一个解，则m的值是（）

A、﹣4 B、4 C、0 D、0或4

查看试题解析
4. 要得到抛物线 $y = \frac{1}{2} {(x - 6)}^{2} + 3$ ，可以将抛物线 $y = \frac{1}{2} x^{2}$ （）

A、向右平移6个单位长度，再向下平移3个单位长度 B、向右平移6个单位长度，再向上平移3个单位长度 C、向左平移6个单位长度，再向上平移3个单位长度 D、向左平移6个单位长度，再向下平移3个单位长度

查看试题解析
5. 如图，△OAB的边OB在x轴上，点B坐标为（2，0），以点O为旋转中心，把△OAB逆时针旋转90°，则旋转后点B的对应点的坐标是（）.

A、（2，0） B、（-2，0） C、（0，2） D、（0，-2）

查看试题解析
6. 如图，AB是⊙O直径，若∠AOC＝140°，则∠D的度数是（）

A、20° B、30° C、40° D、70°

查看试题解析
7. 小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表：

抛掷次数

100

200

300

400

500

正面朝上的频数

53

98

156

202

244

若抛掷硬币的次数为1000，则“正面朝上”的频数最接近（）

A、20 B、300 C、500 D、800

查看试题解析
8. 如图，AC、BD是⊙O的两条相交弦，∠ACB＝∠CDB＝60°，AC＝ $2 \sqrt{3}$ ，则⊙O的直径是（）

A、2 B、4 C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析
9.
如图，用一张半径为24cm的扇形纸板制作一顶圆锥形帽子（接缝忽略不计），如果圆锥形帽子的底面半径为10cm，那么这张扇形纸板的面积是（　　）

A、240πcm² B、480πcm² C、1200πcm² D、2400πcm²

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的顶点坐标为 $(- 1 ， n)$ ，其部分图象如图所示．以下结论错误的是（）

A、 $a b c > 0$ B、 $4 a c - b^{2} < 0$ C、 $3 a + c > 0$ D、关于x的方程 $a x^{2} + b x + c - n = 1$ 无实数根

查看试题解析

二、填空题

11. 已知点A（a，﹣1）与点B（1，b）关于原点对称，则a+b＝.

查看试题解析
12. 若关于 $x$ 的方程 $(m + 2) x^{2} + x + m^{2} - 1 = 0$ 是一元二次方程，则 $m$ 的取值范围是
.

查看试题解析
13. 已知x=1是一元二次方程x²＋ax－b=0的一个根，则代数式a²＋b²－2ab的值是.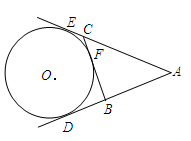

查看试题解析
14. 如图， $A D$ 、 $A E$ 、 $C B$ 均为⊙ $O$ 的切线， $D 、 E 、 F$ 分别是切点， $A D = 5$ ，则 $Δ A B C$ 的周长为．

查看试题解析

三、解答题

15. 解方程， $x^{2} + 2 x - 3 = 0$ .

查看试题解析
16. 已知二次函数y＝x²＋ax＋3的图象经过点P(-2，3)，

(1)、求a的值和图象的顶点坐标.

(2)、点Q(m，n)在该二次函数的图象上，当m＝2时，求n的值.

查看试题解析
17. 如图AB是⊙O的直径，弦CD⊥AB于点E，若EB＝9，AE＝1，求弦CD的长.

查看试题解析
18. 已知a，b，c是△ABC的三边长，且方程 $(a^{2} + b^{2}) x^{2} - 2 c x + 1 ＝ 0$ 有两个相等的实数根.请你判断△ABC的形状.

查看试题解析
19. 如图，方格纸中每个小正方形的边长都是1个单位长度，在方格纸中建立如图所示的平面直角坐标系.△ABC的顶点都在格点上.

（ 1 ）将△ABC向右平移6个单位长度得到△A₁B₁C₁ ，请画出△A₁B₁C₁；

（ 2 ）画出△A₁B₁C₁关于点O的中心对称图形△A₂B₂C₂：

（ 3 ）若将△ABC绕某一点旋转可得到△A₂B₂C₂ ，请直接写出旋转中心的坐标.

查看试题解析
20. 小红和小丁玩纸牌游戏，如图是同一副扑克中的4张牌的正面，将它们正面朝下洗匀后放在桌面上.

(1)、小红从4张牌中抽取一张，这张牌的数字为偶数的概率是；

(2)、小红先从中抽出一张，小丁从剩余的3张牌中也抽出一张，比较两人抽取的牌面上的数字，数字大者获胜，请用树秋图或列表法求出的小红获胜的概率.

查看试题解析
21. 胡师傅今年开了一家煮品店， 5月份盈利3600元，7月份盈利5184元，且从5月到7月份，每月盈利的平均增长率相同.

(1)、求每月盈利的平均增长率.

(2)、按照这个平均增长率，预计8月份胡师傅的煮品店盈利将达到多少元？

查看试题解析
22. 如图，以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF，连结BE、CF.

(1)、求证：△FAC≌△BAE；

(2)、图中可以通过旋转△BAE而得到△FAC，请你说出旋转中心、旋转方向和旋转角的度数.

查看试题解析
23. “共和国勋章”是中华人民共和国的最高荣誉勋章.在2019年获得“共和国勋章”的八位杰出人物中，有于敏、孙家栋、袁隆平、黄旭华四位院士.如图是四位院士（依次记为A，B，C，D）为让同学们了解四位院士的贡献，老师设计如下活动：取四张完全相同的卡片，分别写上A，B，C，D四个标号，然后背面朝上放置，搅匀后每个同学可从中随机抽取一张，记下标号后放回，老师要求每位同学根据抽到的卡片上的标号查找相应院士的资料制作小报，求小明和小华查找同一位院士资料的概率.
A． B． C． D．

查看试题解析
24. 如图，以△ABC的边BC为直径的⊙O，交AB边于点D，D为AB的中点，DE⊥AC于点E.

(1)、求证：AC=BC.

(2)、求证：DE是⊙O的切线.

查看试题解析
25. 如图，抛物线y=﹣x²+bx+c与x轴交于A、B两点（点A在点B的左侧），点A的坐标为（﹣1，0），与y轴交于点C（0，3），作直线BC.动点P在x轴上运动，过点P作PM⊥x轴，交抛物线于点M，交直线BC于点N，设点P的横坐标为m.

(1)、求抛物线的解析式和直线BC的解析式；

(2)、当点P在线段OB上运动时，求线段MN的最大值；

(3)、当以C、O、M、N为顶点的四边形是平行四边形时，直接写出m的值.

查看试题解析

抛掷次数	100	200	300	400	500
正面朝上的频数	53	98	156	202	244