辽宁省大连市甘井子区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期：2021-03-09 类型：期末考试
一、单选题
-
1. 下列几何图形中，不是轴对称图形的是（ ）A、
平行四边形
B、
圆
C、
等腰三角形
D、
等边三角形
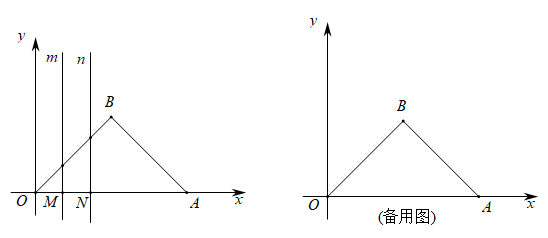
2. 下列长度的三条线段能组成三角形的是（ ）A、3，4，8 B、5，6，11 C、3，4，7 D、5，6，103. 世界最大的单口径球面射电望远镜被誉为“中国天眼”，在其新发现的脉冲星中有一颗毫秒脉冲星的自转周期为0.00519秒，数字0.00519用科学记数法可以表示为（ ）A、0.519×10﹣3 B、5.19×10﹣3 C、5.19×10﹣4 D、5.19×10﹣54. 若分式 中x和y的值都扩大到原来的2倍，则分式的值（ ）A、扩大到原来的2倍 B、扩大到原来的4倍 C、缩小到原来的 D、不变5. 下列运算正确的是（ ）A、x2•x3＝x5 B、（x2）3＝x5 C、6x6÷3x2＝2x3 D、x3+x3＝2x66. 若x2+mx+9＝（x﹣3）2 ， 则m的值为（ ）A、6 B、﹣6 C、±6 D、37. 等腰三角形的一个内角为120°，则底角的度数为（ ）A、30° B、40° C、60° D、120°8. 如图，电信部门要在公路l旁修建一座移动信号发射塔.按照设计要求，发射塔到两个城镇M，N的距离必须相等，则发射塔应该建（ ）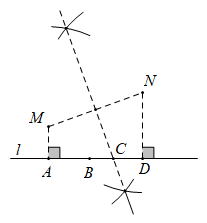
A、A处 B、B处 C、C处 D、D处9. 如图，对一个正方形进行面积分割，下列等式能够正确表示该图形面积关系的是（ ）
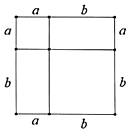A、（a+b）2＝a2+2ab+b2 B、（a+b）2＝a2+2ab﹣b2 C、（a﹣b）2＝a2﹣2ab+b2 D、（a+b）（a﹣b）＝a2﹣b210. 如图，AC⊥BC，BD⊥AD，垂足分别为C，D，再添加一个条件，仍不能判定△ABC≌△BAD的是（ ）
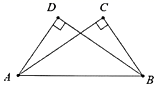A、AC＝BD B、AD＝BC C、∠ABD＝∠BAC D、∠CAD＝∠DBC二、填空题
-
11. 计算：3﹣2= ．12. 若分式 有意义，则 的取值范围是.13. 分解因式：x2﹣2x= ．14. 如图，则x的值为.
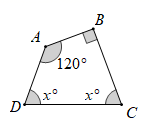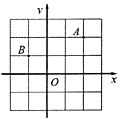
15. 如图，是屋架设计图的一部分，点D是斜梁AB的中点，立柱BC，DE分别垂直于横梁AC，若DE＝1.8m，∠A＝30°，则斜梁AB的长为m.
16. 如图所示的平面直角坐标系中，点A坐标为（2，2），点B坐标为（﹣1，1），在x轴上有点P，使得AP+BP最小，则点P的坐标为.
三、解答题
-
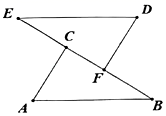
17.(1)、计算：4（x+1）2﹣（2x﹣3）（2x+3）(2)、分解因式：x2y﹣4y18. 解方程： ＝ +119. 先化简，再求值： ÷ ，其中x＝3.20. 如图，点E，C，F，B在同一条直线上，EC＝BF，AC∥DF，∠A＝∠D.
求证：AB＝DE.
21. 为了防止感染新冠病毒，小明家要购买A，B两种型号的口罩，每个A型号口罩比B型号口罩的单价少0.3元，且用45元购买的A型口罩与用60元购买的B型口罩数量相同，求两种口罩的单价.22. 如图，在平面直角坐标系中，点A（4，4），点B（0，2），连接AB，AO.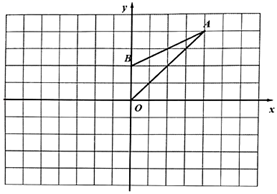
(1)、坐标系中有点C，使得△COB≌△AOB；①在坐标系中画出△BOC；
②点C坐标为；
(2)、若x轴上有点D，使得△ABD是以AB为腰的等腰三角形，则点D的坐标为（写出一个结果即可）.23. 例：解不等式（x﹣2）（x+3）＞0解：由实数的运算法则：“两数相乘，同号得正”
得① ，或② ，
解不等式组①得，x＞2，
解不等式组②得，x＜﹣3，
所以原不等式的解集为x＞2或x＜﹣3.
阅读例题，尝试解决下列问题：
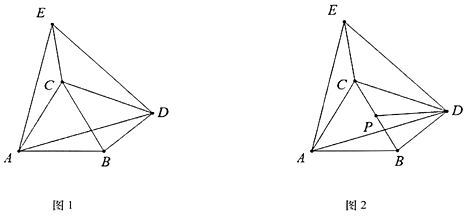
(1)、平行运用：解不等式x2﹣9＞0；(2)、类比运用：若分式 的值为负数，求x的取值范围.24. 在日历上，我们可以发现其中某些数满足一定的规律，如图1是2021年1月份的日历，任意选择图中所示的方框，每个框四个角上的数交叉相乘后求和，再与中间的数的平方的2倍作差，例如：3×l9+5×17﹣2×112＝﹣100，14×30+16×28﹣2×222＝﹣100，不难发现，结果都是﹣100.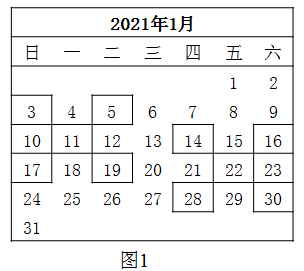
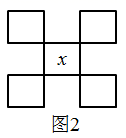(1)、如图2，设日历中所示图形中间的数字为x，请用含x的式子表示发现的规律；(2)、利用整式的运算对（1）中的规律加以证明.
