广西南宁市2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，可以看作是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 某种冠状病毒的直径是120纳米，1纳米＝ $10^{- 9}$ 米，则这种冠状病毒的直径是（）厘米.

A、 $120 \times 10^{- 9}$ B、 $1.2 \times 10^{- 7}$ C、 $1.2 \times 10^{- 6}$ D、 $1.2 \times 10^{- 5}$

查看试题解析
3. 有 2cm 和 3cm 的两根小棒，请你再找一根小棒，并以这三根小棒为边围成一个三角形，下列长度的小棒不符合要求的是（）.

A、2cm B、3cm C、4cm D、5cm

查看试题解析
4. 下列化简正确的是（）

A、 $\frac{m - n}{- m - n} = \frac{n - m}{m + n}$ B、 $\frac{a^{2} + b^{2}}{b^{2} + a b} = \frac{a}{b}$ C、 $\frac{- 14 m n^{2} k}{4 m^{2} n} = - \frac{7 k}{2}$ D、 $\frac{1 - x^{2}}{x^{2} - 2 x + 1} = \frac{x + 1}{x - 1}$

查看试题解析
5. 点P（x，y）关于直线x=1的对称点P₁坐标是（）

A、 $(- x + 2, y)$ B、 $(x, 2 - y)$ C、 $(- x - 2, y)$ D、 $(x, - 2 - y)$

查看试题解析
6. 如图所示， $B D$ 是 $△ A B C$ 的角平分线， $D E / / B C$ 交AB于点E， $∠ A = 45^{°} ， ∠ B D C = 60^{°}$ ，则 $∠ C$ 的度数是（）

A、 $100^{°}$ B、 $105^{°}$ C、 $110^{°}$ D、 $115^{°}$

查看试题解析
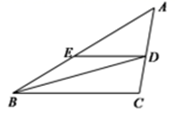7. 下列计算正确的是（）

A、x²+x＝x³ B、x²﹣2x²＝x² C、2x•3x²＝6x² D、x（x²﹣1）＝x³﹣x

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ A = 80 °$ ，高BE和CH的交点为O，则∠BOC=（）

A、80° B、120° C、100° D、150°

查看试题解析
9. 若（a^mbⁿ）³=a⁹b¹⁵ ，则m、n的值分别为（）

A、9；5 B、3；5 C、5；3 D、6；12

查看试题解析
10. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ，若 $A C + B C = 50$ ， $D E$ 为 $A B$ 的垂直平分线，则 $Δ A C D$ 的周长为（）

A、 $25$ B、 $45$ C、 $50$ D、 $55$

查看试题解析
11. 一个容器盛满酒精，第一次倒出10升后，用水加满，第二次倒出6升后，再用水加满，这时容器内的酒精与水的体积之比为7：13，则这个容器的容积为（）

A、18升 B、20升 C、24升 D、30升

查看试题解析
12. 如图，在△ABC中，∠BAC和∠ABC的平分线AE，BF相交于点O，AE交BC于E，BF交AC于F，过点O作OD⊥BC于D，下列四个结论：①∠AOB＝90°+ $\frac{1}{2}$ ∠C；②当∠C＝60°时，AF+BE＝AB； ③若OD＝a，AB+BC+CA＝2b，则S_△ABC＝ab.其中正确的是（）

A、①② B、②③ C、①②③ D、①③

查看试题解析

二、填空题

13. 当 $x$ 时，分式 $\frac{1 - x}{2 x + 1}$ 有意义.

查看试题解析
14. 若△ABC中，∠ACB是钝角，AD是BC边上的高，若AD＝2，BD＝3．CD＝1，则△ABC的面积等于．

查看试题解析
15. 已知一个n边形的内角和等于1980°，则n= ．

查看试题解析
16. 在实数范围内分解因式：xy²﹣4x＝.

查看试题解析
17. 如图，已知△ABC≌△ADE，若AB=9，AC=4，则BE的值为.

查看试题解析
18. 我国宋朝数学家杨辉在他的著作 $《$ 解：九章算法 $》$ 中提出“杨辉三角” $($ 如图 $)$ ，此图揭示了 ${(a + b)}^{n} (n$ 为非负整数 $)$ 展开式的项数及各项系数的有关规律.

例如： ${(a + b)}^{0} = 1$ ，它只有一项，系数为1；系数和为1；

${(a + b)}^{1} = a + b$ ，它有两项，系数分别为1，1，系数和为2；

${(a + b)}^{2} = a^{2} + 2 ab + b^{2}$ ，它有三项，系数分别为1，2，1，系数和为4；

${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 {ab}^{2} + b^{3}$ ，它有四项，系数分别为1，3，3，1，系数和为8； $\dots$ ，

则 ${(a + b)}^{n}$ 的展开式共有项，系数和为.

查看试题解析

三、解答题

19. 计算：（2a﹣3b）²﹣（3a﹣2b）².

查看试题解析
20. 先化简： $\frac{x^{2} - 1}{x^{2} - 2 x + 1} + \frac{x}{x^{2} + 1} \div \frac{x - 1}{x + 1}$ ，再从﹣1≤x≤2的整数中选取一个你喜欢的x的值代入求值.

查看试题解析
21. 如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．

(1)、在图中画出与△ABC关于直线l成轴对称的△A′B′C′；

(2)、在直线l上找一点P（在答题纸上图中标出），使PB+PC的长最短，这个最短长度的平方值是．

查看试题解析
22. 已知：如图，点A，B，C，D在同一直线上，AE∥DF，BF∥EC，AB=CD．求证：AE=DF.

查看试题解析
23. 图 $a$ 是一个长为 $2 m$ ，宽为 $2 n$ 的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图的形状拼成一个正方形.

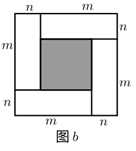(1)、请求图b中的大正方形的边长为，阴影部分正方形的边长为；

(2)、请用两种不同的方法求图中阴影部分的面积；

(3)、观察图b，请写出 ${(m + n)}^{2}$ 、 ${(m - n)}^{2}$ 、 $m n$ 这三个代数式之间的等量关系；

(4)、若 $m + n = 5$ ， $m - n = 3$ ，求 $m n$ 的值.

查看试题解析
24. 如图，在 $△ A B C$ 中， $A B = A C = 3$ ， $∠ B = ∠ C = 50^{\circ}$ ，点D在边BC上运动（点D不与点 $B ， C$ 重合），连接AD，作 $∠ A D E = 50^{\circ}$ ，DE交边AC于点E.

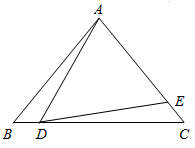(1)、当 $∠ B D A = 100^{\circ}$ 时， $∠ E D C =$ $^{\circ}$ ， $∠ D E C =$ $^{\circ}$

(2)、当DC等于多少时， $△ A B D ≌ △ D C E$ ，请说明理由；

(3)、在点D的运动过程中， $△ A D E$ 的形状可以是等腰三角形吗？若可以，请求出 $∠ B D A$ 的度数；若不可以，请说明理由.

查看试题解析
25. 疫情防控形势下，人们在外出时都应戴上口罩以保护自己免受新型冠状病毒感染.某药店用4000元购进若干包一次性医用口罩，很快售完，该店又用 $7500$ 元钱购进第二批这种口罩，所进的包数比第一批多 $50 %$ ，每包口罩的进价比第一批每包口罩的进价多 $0.5$ 元，请解答下列问题：

(1)、求购进的第一批医用口罩有多少包；

(2)、政府采取措施，在这两批医用口罩的销售中，售价保持了一致.若售完这两批口罩的总利润不高于 $3500$ 元钱，那么药店销售该口罩每包的最高售价是多少元？

查看试题解析
26. 已知点C是∠MAN平分线上一点，∠BCD的两边CB、CD分别与射线AM、AN相交于B，D两点，且∠ABC+∠ADC＝180°.过点C作CE⊥AB，垂足为E.

(1)、如图1，当点E在线段AB上时，求证：BC＝DC；

(2)、如图2，当点E在线段AB的延长线上时，探究线段AB、AD与BE之间的等量关系；

(3)、如图3，在（2）的条件下，若∠MAN＝60°，连接BD，作∠ABD的平分线BF交AD于点F，交AC于点O，连接DO并延长交AB于点G.若BG＝1，DF＝2，求线段DB的长.

查看试题解析