甘肃省平凉市崆峒区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.0000000076克,将数0.0000000076用科学记数法表示为( )A、7.6×10﹣9 B、7.6×10﹣8 C、7.6×109 D、7.6×1083. 如图, 是 的外角,若 , ,则 ( )
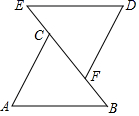
2. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.0000000076克,将数0.0000000076用科学记数法表示为( )A、7.6×10﹣9 B、7.6×10﹣8 C、7.6×109 D、7.6×1083. 如图, 是 的外角,若 , ,则 ( ) A、40° B、50° C、60° D、70°4. 若 有意义,则a的取值范围是( )A、a=﹣1 B、a≠﹣1 C、a= D、a≠5. 下列运算正确的是( )A、 B、 C、 D、6. 若(x+m)2=x2+kx+16,则m的值为( )A、4 B、±4 C、8 D、±87. 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使 ,连接BC并延长到点E,使 ,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到 ,理由是( )
A、40° B、50° C、60° D、70°4. 若 有意义,则a的取值范围是( )A、a=﹣1 B、a≠﹣1 C、a= D、a≠5. 下列运算正确的是( )A、 B、 C、 D、6. 若(x+m)2=x2+kx+16,则m的值为( )A、4 B、±4 C、8 D、±87. 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使 ,连接BC并延长到点E,使 ,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到 ,理由是( ) A、SSS B、AAS C、ASA D、SAS8. 如图,在等腰三角形ABC中,∠BAC=120°,DE是AB的垂直平分线,线段DE=1cm,则BC的长度为( )
A、SSS B、AAS C、ASA D、SAS8. 如图,在等腰三角形ABC中,∠BAC=120°,DE是AB的垂直平分线,线段DE=1cm,则BC的长度为( ) A、8cm B、4cm C、6cm D、10cm9. 如图,已知OA=OB=OC,BC∥AO,若∠A=36°,则∠B等于( )
A、8cm B、4cm C、6cm D、10cm9. 如图,已知OA=OB=OC,BC∥AO,若∠A=36°,则∠B等于( ) A、54° B、60° C、72° D、76°10. 下列说法:①解分式方程一定会产生增根;②方程 的根为2;③方程 的最简公分母为 ;④ 是分式方程.其中正确的个数是( )A、1 B、2 C、3 D、4
A、54° B、60° C、72° D、76°10. 下列说法:①解分式方程一定会产生增根;②方程 的根为2;③方程 的最简公分母为 ;④ 是分式方程.其中正确的个数是( )A、1 B、2 C、3 D、4二、填空题
-
11. 计算:(﹣3)0= .12. 如果一个正多边形的一个外角是60°,那么这个正多边形的边数是.13. 如图, , , ,则 .
 14. 因式分解:﹣8ax2+16axy﹣8ay2= .15. 如图, ABC中, ,DE是AB的垂直平分线,垂足为D,交AC于E.若 , BCE的周长为17cm,则BC=cm.
14. 因式分解:﹣8ax2+16axy﹣8ay2= .15. 如图, ABC中, ,DE是AB的垂直平分线,垂足为D,交AC于E.若 , BCE的周长为17cm,则BC=cm. 16. 如图,在Rt△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,BD=6,则CD的长为.
16. 如图,在Rt△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,BD=6,则CD的长为.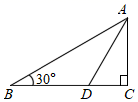 17. 若关于x的分式方程 有增根,则m的值为.18. 如图,在平面直角坐标系中, , ,点P是x轴上任意一点,当 有最小值时,P点的坐标为.
17. 若关于x的分式方程 有增根,则m的值为.18. 如图,在平面直角坐标系中, , ,点P是x轴上任意一点,当 有最小值时,P点的坐标为.
三、解答题
-
19. 计算: .20. 解分式方程:21. 如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等.
 22. 如图,已知在 ABC中,BD是∠ABC的角平分线, , ,求∠DBC的度数.
22. 如图,已知在 ABC中,BD是∠ABC的角平分线, , ,求∠DBC的度数. 23. 请认真观察图形,解答下列问题:
23. 请认真观察图形,解答下列问题:
 (1)、根据图①中条件,请用两种不同方法表示两个阴影图形的面积的和;(2)、在(1)的条件下,如图②,两个正方形边长分别为a,b,如果 ,求阴影部分的面积.24. 如图, , ,AC与BD相交于点O. 求证: .
(1)、根据图①中条件,请用两种不同方法表示两个阴影图形的面积的和;(2)、在(1)的条件下,如图②,两个正方形边长分别为a,b,如果 ,求阴影部分的面积.24. 如图, , ,AC与BD相交于点O. 求证: . 25. 某种产品的原料提价,因而厂家决定对产品进行提价,现有三种方案:
25. 某种产品的原料提价,因而厂家决定对产品进行提价,现有三种方案:①第一次提价p%,第二次提价q%;
②第一次提价q%,第二次提价p%;
③第一、二次提价均为 .
其中p,q是不相等的正数,三种方案哪种提价最多?
26. 如图, 于 , 于 ,若 , . (1)、求证: 平分 ;(2)、已知 , ,求 的长.27. 生活垃圾处理是关系民生的基础性公益事业,加强生活垃圾分类处理,维护公共环境和节约资源是全社会共同的责任,某小区购进A型和B型两种分类垃圾桶,购买A型垃圾桶花费了2500元,购买B型垃圾桶花费了2000元,且购买A型垃圾桶数量是购买B型垃圾桶数量的2倍,已知购买一个B型垃圾桶比购买一个A型垃圾桶多花30元.(1)、求购买一个A型垃圾桶、一个B型垃圾桶各需多少元?(2)、若小区一次性购买A型,B型垃圾桶共60个,要使总费用不超过4000元,最少要购买多少个A型垃圾桶?28. 如图,在等边 ABC中,点D,E分别是边AC,AB上的点,且 ,BD交CE于点P.
(1)、求证: 平分 ;(2)、已知 , ,求 的长.27. 生活垃圾处理是关系民生的基础性公益事业,加强生活垃圾分类处理,维护公共环境和节约资源是全社会共同的责任,某小区购进A型和B型两种分类垃圾桶,购买A型垃圾桶花费了2500元,购买B型垃圾桶花费了2000元,且购买A型垃圾桶数量是购买B型垃圾桶数量的2倍,已知购买一个B型垃圾桶比购买一个A型垃圾桶多花30元.(1)、求购买一个A型垃圾桶、一个B型垃圾桶各需多少元?(2)、若小区一次性购买A型,B型垃圾桶共60个,要使总费用不超过4000元,最少要购买多少个A型垃圾桶?28. 如图,在等边 ABC中,点D,E分别是边AC,AB上的点,且 ,BD交CE于点P. (1)、如图①,求证: ;(2)、点M是边BC的中点,连接PA,PM. 如图②,若点A,P,M三点共线,求证: .
(1)、如图①,求证: ;(2)、点M是边BC的中点,连接PA,PM. 如图②,若点A,P,M三点共线,求证: .