甘肃省酒泉市金塔县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
1. 的平方根是( )A、4 B、2 C、 D、2. 以下列各组数为三边的三角形中不是直角三角形的是 ( )A、1,2, B、3,5,4 C、5,12,13 D、1,3,3. 在给出的一组数0,π, , 3.14, , 中,无理数有( )A、1个 B、2个 C、3个 D、5个4. 下列计算正确的是( )A、 B、 C、 D、5. 甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如表:
选手
甲
乙
丙
丁
平均数(环)
9.2
9.2
9.2
9.2
方差(环2)
0.35
0.15
0.25
0.27
则这四个中,成绩发挥最稳定的是( )
A、甲 B、乙 C、丙 D、丁6. 下列四点中,在函数y=3x+2的图象上的点是( )A、(-1,1) B、(-1,-1) C、(2,0) D、(0,-1.5)7. 用长为50的栏杆围成一个长为x宽为y的长方形,则y与x的函数关系为( )A、y=25-x B、y=25+x C、y=50-x D、y=50+x8.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
 A、30° B、25° C、20° D、15°9. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=kx+k的图象大致是( )A、
A、30° B、25° C、20° D、15°9. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=kx+k的图象大致是( )A、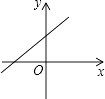 B、
B、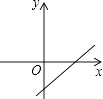 C、
C、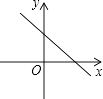 D、
D、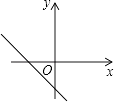 10. 甲、乙两人参加植树活动,两人共植树20棵,已知甲植树数是乙的1.5倍.如果设甲植树x棵,乙植树y棵,那么可以列方程组( )A、 B、 C、 D、
10. 甲、乙两人参加植树活动,两人共植树20棵,已知甲植树数是乙的1.5倍.如果设甲植树x棵,乙植树y棵,那么可以列方程组( )A、 B、 C、 D、二、填空题
-
11. 化简: = .12. 比较大小:- 4.(填“<”或“>”符号)13. 点A(﹣3,2)关于y轴的对称点坐标是 .
14. 点P在第二象限内,P到x轴的距离是3,到y轴的距离是5,那么点 的坐标为.15. 已知a、b满足 ,则(a+b)2021的值为.16. 已知一组数据1,7,10,8, ,6,0,3,若 ,则 应等于.17. 如图,AB∥CD,点E在线段BC上,若∠B=40°,∠D=30°,则∠BED的度数是.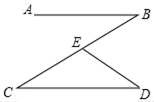 18. 已知函数y=ax+b和y=kx+m的图象交于点A,则根据图象可知,关于x,y的二元一次方程组 的解是.
18. 已知函数y=ax+b和y=kx+m的图象交于点A,则根据图象可知,关于x,y的二元一次方程组 的解是. 19. “等角的补角相等”的条件是 ,结论是 .20. 如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,则点C到AB的距离CD= .
19. “等角的补角相等”的条件是 ,结论是 .20. 如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,则点C到AB的距离CD= .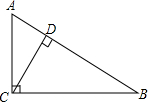
三、解答题
-
21. 计算题:(1)、(2)、22. 解方程组:(1)、 ;(2)、23. 在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上。在建立平面直角坐标系后,点B的坐标为(-1,2).
 (1)、把△ABC向下平移8个单位后得到对应的△ ,画出△ ,并写出 坐标;(2)、以原点O为对称中心,画出与△ 关于原点O对称的△ ,并写出点 的坐标.24. 如图,已知:∠DGA=∠FHC,∠A=∠F.求证:DF∥AC.(注:证明时要求写出每一步的依据)
(1)、把△ABC向下平移8个单位后得到对应的△ ,画出△ ,并写出 坐标;(2)、以原点O为对称中心,画出与△ 关于原点O对称的△ ,并写出点 的坐标.24. 如图,已知:∠DGA=∠FHC,∠A=∠F.求证:DF∥AC.(注:证明时要求写出每一步的依据) 25. 某公司要把240吨矿石运往 、 两地,现用大、小两种货车共20辆,恰好能一次性装完这批矿石.已知这两种货车的载重量分别为15吨/辆和10吨/辆,求这两种货车各用多少辆?26. 为了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图甲、乙所示的两个统计图(部分未完成).请根据图中信息,回答下列问题:
25. 某公司要把240吨矿石运往 、 两地,现用大、小两种货车共20辆,恰好能一次性装完这批矿石.已知这两种货车的载重量分别为15吨/辆和10吨/辆,求这两种货车各用多少辆?26. 为了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图甲、乙所示的两个统计图(部分未完成).请根据图中信息,回答下列问题: (1)、校团委随机调查的学生人数是 , 请你补全条形统计图;(2)、表示“50元”的扇形所占百分数是 , 被调查的学生每人一周零花钱数额的中位数是 , 众数.(3)、为捐助贫困山区儿童学习,全校1000名学生每人自发地捐出一周的零花钱,请估算全校学生共捐款多少元?
(1)、校团委随机调查的学生人数是 , 请你补全条形统计图;(2)、表示“50元”的扇形所占百分数是 , 被调查的学生每人一周零花钱数额的中位数是 , 众数.(3)、为捐助贫困山区儿童学习,全校1000名学生每人自发地捐出一周的零花钱,请估算全校学生共捐款多少元?

