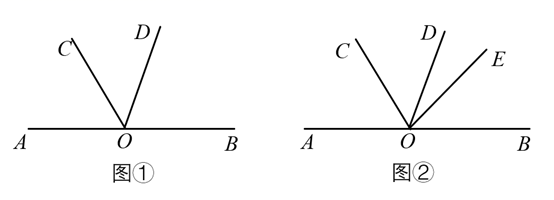天津市河西区2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-03-08 类型:期末考试
一、单选题
-
1. 计算 的结果为( )A、27 B、-27 C、18 D、-182. 若 ,则x的值为( )A、5 B、5或-5 C、-25 D、253. 如图所示的平面图形绕轴旋转一周,可得到的立体图形是( )
 A、
A、 B、
B、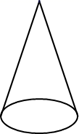 C、
C、 D、
D、 4. 如图,下列说法中错误的是( )
4. 如图,下列说法中错误的是( ) A、 与 是同一个角 B、 与 是同一个角 C、 也可以表示为 D、5. 下列说法中错误的是( )A、两点的所有连线中,线段最短 B、连接两点间的线段的长度,叫做这两点的距离 C、灯塔在货轮的西北方向,表示灯塔在货轮的北偏西45°方向 D、时钟8:30这一时刻,时钟上的时针和分针之间的夹角为6. 如图所示的图形经过折叠可以得到一个正方体,则与“体”字一面相对的面上的字是( )
A、 与 是同一个角 B、 与 是同一个角 C、 也可以表示为 D、5. 下列说法中错误的是( )A、两点的所有连线中,线段最短 B、连接两点间的线段的长度,叫做这两点的距离 C、灯塔在货轮的西北方向,表示灯塔在货轮的北偏西45°方向 D、时钟8:30这一时刻,时钟上的时针和分针之间的夹角为6. 如图所示的图形经过折叠可以得到一个正方体,则与“体”字一面相对的面上的字是( )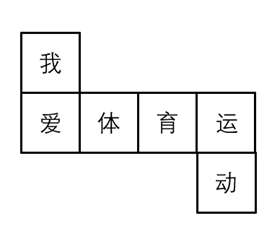 A、我 B、育 C、运 D、动7. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )A、
A、我 B、育 C、运 D、动7. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )A、 B、
B、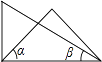 C、
C、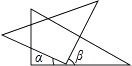 D、
D、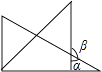 8. 如图.将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为
8. 如图.将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为 A、15° B、30° C、45° D、60°9. 如图,有理数a , b , c , d在数轴上的对应点分别是A , B , C , D , 若 ,则a+c( )
A、15° B、30° C、45° D、60°9. 如图,有理数a , b , c , d在数轴上的对应点分别是A , B , C , D , 若 ,则a+c( ) A、大于5 B、小于5 C、等于5 D、不能确定10. “某学校七年级学生人数为n , 其中男生占55%,女生共有110人.”下列方程能表示上述语句中的相等关系的有( )
A、大于5 B、小于5 C、等于5 D、不能确定10. “某学校七年级学生人数为n , 其中男生占55%,女生共有110人.”下列方程能表示上述语句中的相等关系的有( )① ;② ;③ ;④ ;⑤
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 计算 的结果等于 .12. 如图,将一个圆形的蛋糕等分成六份,则每一份中的角的度数为 .
 13. 计算: 的结果为 .14. 若某数除以4再减去2,等于这个数的 加上8,则这个数为 .15. 某轮船顺水航行 3h,逆水航行 1.5h,已知轮船在静水中的速度为 a km/h,水流速度是 y km/h,则轮船共航行km.16. 已知四个数的和是100,如果第一个数加上4,第二个数减去4,第三个数乘以4,第四个数除以4,得到的这四个新数恰好都相等,则这四个数分别是 .
13. 计算: 的结果为 .14. 若某数除以4再减去2,等于这个数的 加上8,则这个数为 .15. 某轮船顺水航行 3h,逆水航行 1.5h,已知轮船在静水中的速度为 a km/h,水流速度是 y km/h,则轮船共航行km.16. 已知四个数的和是100,如果第一个数加上4,第二个数减去4,第三个数乘以4,第四个数除以4,得到的这四个新数恰好都相等,则这四个数分别是 .三、解答题
-
17. 解方程: .18. 点A,B,C,D的位置如图,按下列要求画出图形:
 (1)、画直线 ,直线 ,它们相交于点E;(2)、连接 ,连接 ,它们相交于点O;(3)、画射线 ,射线 ,它们相交于点F.19. 如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
(1)、画直线 ,直线 ,它们相交于点E;(2)、连接 ,连接 ,它们相交于点O;(3)、画射线 ,射线 ,它们相交于点F.19. 如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.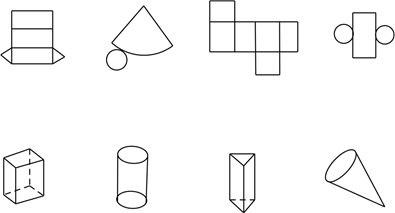 20. 已知数轴上有A,B两个点,分别表示有理数 ,4.
20. 已知数轴上有A,B两个点,分别表示有理数 ,4. (1)、数轴上点A到点B的距离为;
(1)、数轴上点A到点B的距离为;数轴上到点A,B的距离相等的点的位置表示的有理数为;
(2)、若有动点P从点A出发,以每秒1个单位的速度向右移动,设移动时间为t秒.用含t的式子分别表示P点到点A和点B的距离.21. 甲乙两车站间的路程为360km,一列慢车从甲站开出,每小时行驶48km,一列快车从乙站开出,每小时行驶72km.(1)、两车同时开出,相向而行,多少小时相遇?(2)、快车先开出25分钟,两车相向而行,慢车行驶多少小时两车相遇?