山西省太原市2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-03-08 类型:期末考试
一、单选题
-
1. -2020的倒数是( )A、 B、 C、2020 D、-2020
-
2. 下列运算中正确的是( )A、 B、 C、 D、
-
3. 从如图所示的 个小正方形中剪去一个小正方形,使剩余的 个小正方形折叠后能围成一个正方体,则应剪去标记为( )的小正方形
 A、祝或考 B、你或考 C、好或绩 D、祝或你或成
A、祝或考 B、你或考 C、好或绩 D、祝或你或成 -
4. 当前,“低头族”已成为热门话题之一,小颖为了解路边行人步行边低头看手机的情况,她应采用的收集数据的方式是( )A、对学校的同学发放问卷进行调查 B、对在路边行走的学生随机发放问卷进行调查 C、对在路边行走的行人随机发放问卷进行调查 D、对在图书馆里看书的人发放问卷进行调查
-
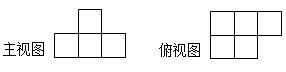
5. 如图所示的主视图和俯视图,其对应的几何体(阴影所示如图)可以是下列( )
 A、
A、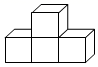 B、
B、 C、
C、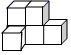 D、
D、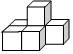
-
6. 如图,数轴上有 , , , 四个整数点(即各点均表示整数),且 .若 , 两点所表示的数分别是 和 ,则线段 的中点所表示的数是( ).
 A、 B、 C、 D、
A、 B、 C、 D、 -
7. 有资料表明,被称为“地球之肺”的森林正以每年15000000公顷的速度从地球上消失,用科学记数法表示15000000是( )A、 B、 C、 D、
-
8. 下列说法中正确的是( )A、若 ,则P是AB的中点 B、若 ,则P是AB的中点 C、若 ,则P为AB的中点 D、若 ,则P是AB的中点
-
9. 如图, ,射线 平分 ,以 为一边作 ,则 的度数为( )
 A、15° B、45° C、15°或30° D、15°或45°
A、15° B、45° C、15°或30° D、15°或45° -
10. 某校举行用火柴棒摆“金鱼”比赛,如图所示:按照上面的规律,摆n个“金鱼”需用火柴棒的根数为( )
 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
11. 已知 ,则 .
-
12. 过一个多边形的一个顶点的对角线有6条,则该多边形是边形.
-
13. 亲爱的同学,现在是北京时间下午2:45,按正常做题速度,你应该做到此题了,此时钟表上的时针和分针的夹角度数是 .
-
14. 如图,C为线段AD上一点,点B为CD的中点,且 , .若点E在AD上,且EA=3cm,BE的长为 .

三、解答题
-
15. 计算:(1)、 ;(2)、先化简,再求值: ,其中 , .
-
16. 解方程:(1)、 ;(2)、 .
-
17. 如图,线段AB,C是线段AB上一点,M是AB的中点,N是AC的中点.若 , ,求线段MN的长;
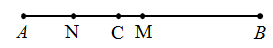
-
18. 初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
 (1)、在这次评价中,一共抽查了名学生;(2)、在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;(3)、请将频数分布直方图补充完整;(4)、如果全市有12000名初三学生,那么在试卷评讲课中,“独立思考”的初三学生约有多少人?
(1)、在这次评价中,一共抽查了名学生;(2)、在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;(3)、请将频数分布直方图补充完整;(4)、如果全市有12000名初三学生,那么在试卷评讲课中,“独立思考”的初三学生约有多少人? -
19. 定义:若 ,则称 与 是关于1的平衡数.(1)、3与是关于1的平衡数, 与(用含 的整式表示)是关于1的平衡数;(2)、若 , ,判断 与 是否是关于1的平衡数,并说明理由.
-
20. 在“清洁乡村”活动中,某村长提出了两种购买垃圾桶方案.
方案一:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用250元;
方案二:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用500元.
设交费时间为x个月,方案一的购买费和垃圾处理费共为M元,方案二的购买费和垃圾处理费共为N元.
(1)、分别用x表示M,N;(2)、若交费时间为12个月,哪种方案更合适,并说明理由.(3)、交费时间为多少个月时,两种方案费用相同? -
21. 十一期间,各大商场掀起购物狂潮,现有甲、乙、丙三个商场开展的促销活动如表所示:
商场
优惠活动
甲
全场按标价的6折销售
乙
实行“满100元送100元的购物券”的优惠,购物券可以在再购买时冲抵现金
(如:顾客购衣服220元,赠券200元,再购买裤子时可冲抵现金,不再送券)
丙
实行“满100元减50元的优惠”(比如:某顾客购物220元,他只需付款120元)
根据以上活动信息,解决以下问题:
(1)、三个商场同时出售一件标价290元的上衣和一条标价270元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场?(2)、黄先生发现在甲、乙商场同时出售一件标价380元的上衣和一条标价300多元的裤子,最后付款额也一样,请问这条裤子的标价是多少元? -
22. 如图,数轴上有A,B两点,所表示的有理数分别为a、b,已知AB=12,原点O是线段AB上的一点,且OA=2OB.
 (1)、a= , b= .(2)、若动点P,Q分别从A,B同时出发,向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,设运动时间为t秒,当点P与点Q重合时,P,Q两点停止运动.
(1)、a= , b= .(2)、若动点P,Q分别从A,B同时出发,向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,设运动时间为t秒,当点P与点Q重合时,P,Q两点停止运动.①当t为何值时,2OP﹣OQ=4;
②当点P到达点O时,动点M从点O出发,以每秒3个单位长度的速度也向右运动,当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后再立即返回,以同样的速度向点Q运动,如此往返,直到点P,Q停止时,点M也停止运动,求在此过程中点M行驶的总路程,并直接写出点M最后位置在数轴上所对应的有理数.
