山西省阳泉市平定县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-03-08 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点( ,6)关于原点对称的点坐标是( )A、( ,2) B、(2, ) C、(2,6) D、( , )2. 下列四个图形是word软件中的自选图形,其中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一元二次方程 的根的情况是( )A、没有实数根 B、只有一个实根 C、有两个相等的实数 D、有两个不相等的实数根4. 对于反比例函数 ,下列说法正确的是( )A、点(1,5)在它的图象上 B、它的图象在第一、三象限 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小5. 从如图所示的扑克牌中任取一张,牌面数字是3的倍数的概率是( )
3. 一元二次方程 的根的情况是( )A、没有实数根 B、只有一个实根 C、有两个相等的实数 D、有两个不相等的实数根4. 对于反比例函数 ,下列说法正确的是( )A、点(1,5)在它的图象上 B、它的图象在第一、三象限 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小5. 从如图所示的扑克牌中任取一张,牌面数字是3的倍数的概率是( ) A、 B、 C、 D、6. 如图,正六边形 内接于 ,连接 ,则 的度数是( )
A、 B、 C、 D、6. 如图,正六边形 内接于 ,连接 ,则 的度数是( )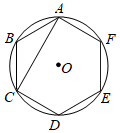 A、 B、 C、 D、7. 如图, ,若 ,则 与 的关系是( )
A、 B、 C、 D、7. 如图, ,若 ,则 与 的关系是( )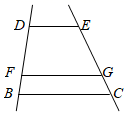 A、 B、 C、 D、8. 如图,在平面直角坐标系中,已知 中点 的坐标为(4,2),以坐标原点 为位似中心,在第三象限内,将 边长放大2倍得到了 ,则点 对应点 的坐标为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,已知 中点 的坐标为(4,2),以坐标原点 为位似中心,在第三象限内,将 边长放大2倍得到了 ,则点 对应点 的坐标为( )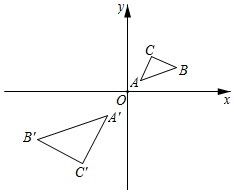 A、( , ) B、( , ) C、( , ) D、(8,4)9. 如图,已知 与 相切于点 ,点 为 上一点, ,过点 作 于点 , 交 于点 ,连接 .已知 ,则图中阴影部分的面积是( )
A、( , ) B、( , ) C、( , ) D、(8,4)9. 如图,已知 与 相切于点 ,点 为 上一点, ,过点 作 于点 , 交 于点 ,连接 .已知 ,则图中阴影部分的面积是( )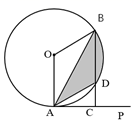 A、 B、 C、π D、10. 如图,二次函数 的图象经过点 (1,0), (4,0),下列说法正确的是( )
A、 B、 C、π D、10. 如图,二次函数 的图象经过点 (1,0), (4,0),下列说法正确的是( )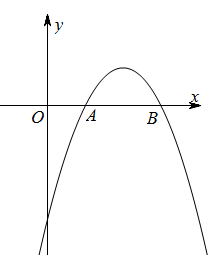 A、 B、 C、图象的对称轴是直线 D、图象的对称轴是直线
A、 B、 C、图象的对称轴是直线 D、图象的对称轴是直线二、填空题
-
11. 两个相似多边形的面积比是9:16,其中较小多边形周长为36cm,则较大多边形周长为 .12. 用16m长的篱笆围成长方形的生物园饲养小兔,设围成长方形的生物园的长为 m,则围成长方形的生物的面积 (单位: )与x的函数表达式是 . (不要求写自变量 的取值范围)
 13. 小明抛掷两枚质地均匀的骰子(如图,骰子的六个面上分别刻有1到6的点数),两枚骰子朝上的点数和是7的概率是 .
13. 小明抛掷两枚质地均匀的骰子(如图,骰子的六个面上分别刻有1到6的点数),两枚骰子朝上的点数和是7的概率是 . 14. 如图,学校综合实践小组的种植园是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为627平方米,设小道的宽为 米,则可列方程为 .
14. 如图,学校综合实践小组的种植园是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为627平方米,设小道的宽为 米,则可列方程为 . 15. 将边长为2的正方形 绕点 按顺时针方向旋转 到 的位置(如图), 与 相交于点 ,则 的长为 . (结果保留根号)
15. 将边长为2的正方形 绕点 按顺时针方向旋转 到 的位置(如图), 与 相交于点 ,则 的长为 . (结果保留根号)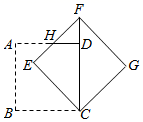
三、解答题
-
16. 解方程:(1)、解方程: ;(2)、解方程: .17. 如图,在平面直角坐标系中,已知 的顶点的坐标分别是 ( ,2), ( ,4), ( ,1).
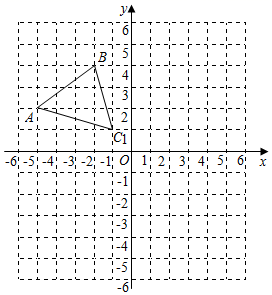 (1)、在图中作出 ,使 和 关于 轴对称;(2)、画出将 以点 为旋转中心,顺时针旋转 对应的 ;(3)、直接写出点 关于点 对称点的坐标.18. 阅读下列内容,并解答问题.
(1)、在图中作出 ,使 和 关于 轴对称;(2)、画出将 以点 为旋转中心,顺时针旋转 对应的 ;(3)、直接写出点 关于点 对称点的坐标.18. 阅读下列内容,并解答问题.一个滑雪者从山坡滑下,为了得出滑行距离 (单位: )与滑行时间 (单位: )之间的关系式,测得一些数据(如表):
滑行时间
0
1
2
4
5
滑行距离
0
4.5
14
28.5
48
为观察 与 之间的关系,建立坐标系(如图),以 为横坐标, 为纵坐标.请解答以下问题:
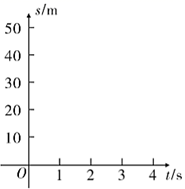 (1)、描出表中数据对应的5个点,并用平滑曲线连接它们;(2)、根据(1)所画出的曲线图象,利用我们所学的函数,近似地表示 关于 的函数关系式.19. 在平面直角坐标系中,直线 ( )与双曲线 ( )相交于 , 两点,点 坐标为(3,2),点 坐标为( , ).
(1)、描出表中数据对应的5个点,并用平滑曲线连接它们;(2)、根据(1)所画出的曲线图象,利用我们所学的函数,近似地表示 关于 的函数关系式.19. 在平面直角坐标系中,直线 ( )与双曲线 ( )相交于 , 两点,点 坐标为(3,2),点 坐标为( , ).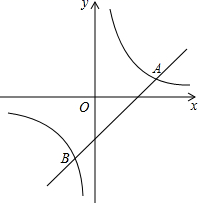 (1)、求一次函数和反比例函数的表达式;(2)、根据函数图象直接写出关于 的不等式 的解集.20. 平定县位于山西中部东侧,是三晋东大门.境内山川秀丽,有著名旅游景区娘子关,有名扬三晋的冠山古书院,建于秦长城一百年之前的周关长城,省级森林公园药林寺等等,这些都是人们周末游的好去处,小明计划某个周末和妹妹一起去旅游,他收集了如图所示四个景点的卡片,卡片分别用N,G,C,Y表示,卡片大小、形状及背面完全相同,通过游戏规则,选择景点,请用列表法或画树状图的方法,求下列随机事件的概率:
(1)、求一次函数和反比例函数的表达式;(2)、根据函数图象直接写出关于 的不等式 的解集.20. 平定县位于山西中部东侧,是三晋东大门.境内山川秀丽,有著名旅游景区娘子关,有名扬三晋的冠山古书院,建于秦长城一百年之前的周关长城,省级森林公园药林寺等等,这些都是人们周末游的好去处,小明计划某个周末和妹妹一起去旅游,他收集了如图所示四个景点的卡片,卡片分别用N,G,C,Y表示,卡片大小、形状及背面完全相同,通过游戏规则,选择景点,请用列表法或画树状图的方法,求下列随机事件的概率: (1)、若选择其中一个景点游戏规则:把这四张图片背面朝上洗匀后,妹妹从中随机抽取一张,作好记录后,将图片放回洗匀,哥哥再抽取一张求两人抽到同一景点的概率;(2)、若选择其中两个景点,游戏规则:把这四张图片背面朝上洗匀后,妹妹和哥哥从中各随机抽取一张(不放回).求两人抽到娘子关和固关长城的概率.21. 如图,已知 是 的直径, 于点 , 是 的切线,切点为 ,连接 ,交 于点 .
(1)、若选择其中一个景点游戏规则:把这四张图片背面朝上洗匀后,妹妹从中随机抽取一张,作好记录后,将图片放回洗匀,哥哥再抽取一张求两人抽到同一景点的概率;(2)、若选择其中两个景点,游戏规则:把这四张图片背面朝上洗匀后,妹妹和哥哥从中各随机抽取一张(不放回).求两人抽到娘子关和固关长城的概率.21. 如图,已知 是 的直径, 于点 , 是 的切线,切点为 ,连接 ,交 于点 .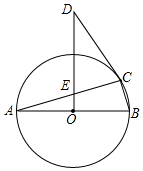 (1)、求证: ;(2)、若 , ,求 的长.22. 问题情境:
(1)、求证: ;(2)、若 , ,求 的长.22. 问题情境:如图1,已知点 是正方形 的中心,以点 为直角顶点的直角三角形 的两边 , 分别过点 , ,且 , , .
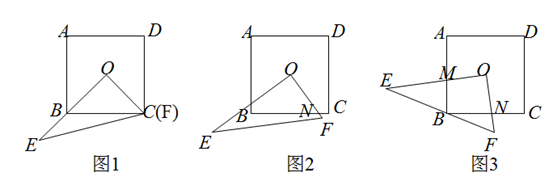 (1)、 的长度为;(2)、操作证明:
(1)、 的长度为;(2)、操作证明:如图2,将 绕点 按顺时针方向旋转,若 , 分别与 , 相交于点 , .请判断 和 有怎样的数量关系,并证明结论;
(3)、探究发现:如图3,将 绕点 按顺时针方向旋转,若点 恰好在 上,求 的度数.
23. 如图,在平面直角坐标系中,已知抛物线 与 轴交于 , 两点,点 在点 的左侧,与 轴交于点 ,其顶点为点 ,点 的坐标为(0, ),该抛物线与 交于另一点 ,连接 .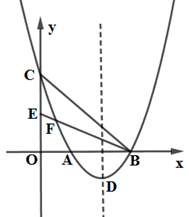 (1)、求点 , , 的坐标;(2)、动点M从点 出发,沿抛物线对称轴方向向下以每秒1个单位的速度运动,运动时间为 ,连接 , ,当 为何值时, 为等腰三角形?(3)、在 轴下方的抛物线上,是否存在点 ,使得 被 平分?若存在,请求出点 的坐标;若不存在,请说明理由.
(1)、求点 , , 的坐标;(2)、动点M从点 出发,沿抛物线对称轴方向向下以每秒1个单位的速度运动,运动时间为 ,连接 , ,当 为何值时, 为等腰三角形?(3)、在 轴下方的抛物线上,是否存在点 ,使得 被 平分?若存在,请求出点 的坐标;若不存在,请说明理由.