山西省吕梁市孝义市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-03-08 类型:期末考试
一、单选题
-
1. 推进生态文明建设,实行垃圾分类和资源化利用是每个公民义不容辞的责任.下列四幅图是垃圾分类标志图案,每幅图案下配有文字说明.则四幅图案中既是轴对称图形,又是中心对称图形的是( )A、有害垃圾
 B、可回收物
B、可回收物  C、厨余垃圾
C、厨余垃圾  D、其他垃圾
D、其他垃圾  2. 关于 的一元二次方程 的根的情况,下列说法正确的是( )A、有一个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根3. 如图是用卡钳测量容器内径的示意图,已知卡钳的四个端点 , , , 到支点 的距离满足 ,且 .现在只要测得卡钳外端 , 两个端点之间的距离,就可以计算出容器的内径 的大小。这种测量原理用到了( )
2. 关于 的一元二次方程 的根的情况,下列说法正确的是( )A、有一个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根3. 如图是用卡钳测量容器内径的示意图,已知卡钳的四个端点 , , , 到支点 的距离满足 ,且 .现在只要测得卡钳外端 , 两个端点之间的距离,就可以计算出容器的内径 的大小。这种测量原理用到了( ) A、图形的旋转 B、图形的平移 C、图形的轴对称 D、图形的相似4. 历史上,数学家们曾做过好多次抛掷硬币的试验,其中一些试验结果如下表所示:
A、图形的旋转 B、图形的平移 C、图形的轴对称 D、图形的相似4. 历史上,数学家们曾做过好多次抛掷硬币的试验,其中一些试验结果如下表所示:实验者
抛掷次数
“正面向上”的次数
“正面向上”的频率
棣莫弗
2048
1061
0.5181
布丰
4040
2048
0.5069
费勒
10000
4979
0.4979
皮尔逊
12000
6019
0.5016
皮尔逊
24000
12012
0.5005
则关于抛掷硬币的试验,下列说法正确的是( )
 A、随着抛掷次数的增加,频率在0.5附近摆动的幅度越来越小 B、随着抛掷次数的增加,频率等于0.5 C、每多抛一次,频率会更加接近0.5 D、无论抛掷多少次,频率与概率都不可能相等5. 如果反比例函数 的图象在第一、三象限内,则下列说法正确的是( )A、 随 的增大而减小 B、 随 的增大而增大 C、 的取值范围为 D、 的取值范围是6. 将抛物线 的向右平移1个单位长度,再向下平移3个单位长度后,得到抛物线的解析式是( )A、 B、 C、 D、7. 如图, 和 是位似图形,点 是位似中心,点 , , 分别是 , , 的中点.若 的面积为 ,周长为 ,则下列说法正确的是( )
A、随着抛掷次数的增加,频率在0.5附近摆动的幅度越来越小 B、随着抛掷次数的增加,频率等于0.5 C、每多抛一次,频率会更加接近0.5 D、无论抛掷多少次,频率与概率都不可能相等5. 如果反比例函数 的图象在第一、三象限内,则下列说法正确的是( )A、 随 的增大而减小 B、 随 的增大而增大 C、 的取值范围为 D、 的取值范围是6. 将抛物线 的向右平移1个单位长度,再向下平移3个单位长度后,得到抛物线的解析式是( )A、 B、 C、 D、7. 如图, 和 是位似图形,点 是位似中心,点 , , 分别是 , , 的中点.若 的面积为 ,周长为 ,则下列说法正确的是( ) A、 的面积为 B、 的面积为 C、 的周长为 D、 的周长为8. 已知二次函数 ,下列说法正确的是( )A、该函数的最小值为2 B、该函数的最小值为1 C、该函数的最大值为2 D、该函数的最大值为19. 近似眼镜的度数 (度)与镜片焦距 (米)之间具有如图所示的反比例函数关系,若要配制一副度数小于400度的近似眼镜,则镜片焦距 的取值范围是( )
A、 的面积为 B、 的面积为 C、 的周长为 D、 的周长为8. 已知二次函数 ,下列说法正确的是( )A、该函数的最小值为2 B、该函数的最小值为1 C、该函数的最大值为2 D、该函数的最大值为19. 近似眼镜的度数 (度)与镜片焦距 (米)之间具有如图所示的反比例函数关系,若要配制一副度数小于400度的近似眼镜,则镜片焦距 的取值范围是( )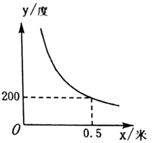 A、0米 米 B、 米 C、0米 米 D、 米10. 如图, 为半圆 的直径,半径 .以 为直径的 交 于点 ,交 于点 ,若 ,则图中阴影部分的面积为( )
A、0米 米 B、 米 C、0米 米 D、 米10. 如图, 为半圆 的直径,半径 .以 为直径的 交 于点 ,交 于点 ,若 ,则图中阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,已知 , , ,那么 的长为 .
 12. 数学课上,老师提出如下问题:“如图,用一段长为 的篱笆围成一个一边靠墙的矩形菜园(墙足够长).这个矩形的长、宽各为多少时,菜园的面积最大?”小慧设菜园的面积为 ,菜园的…为xm,列出 .则自变量x的实际意义是 .
12. 数学课上,老师提出如下问题:“如图,用一段长为 的篱笆围成一个一边靠墙的矩形菜园(墙足够长).这个矩形的长、宽各为多少时,菜园的面积最大?”小慧设菜园的面积为 ,菜园的…为xm,列出 .则自变量x的实际意义是 . 13. 如图, 的顶点 在反比例函数 的图象上,顶点 在 轴的正半轴上,顶点 和 在反比例函数 的图象上,且对角线 轴,则 的面积等于 .
13. 如图, 的顶点 在反比例函数 的图象上,顶点 在 轴的正半轴上,顶点 和 在反比例函数 的图象上,且对角线 轴,则 的面积等于 . 14. 已知函数 图像上两点 ,其中 ,则 (填大于小于或等于).15. 如图所示,复印纸的型号有A0 , A1 , A2 , A3 , A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸沿较长边的中点对折,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似,那么这些型号的复印纸的长、宽之比为 .
14. 已知函数 图像上两点 ,其中 ,则 (填大于小于或等于).15. 如图所示,复印纸的型号有A0 , A1 , A2 , A3 , A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸沿较长边的中点对折,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似,那么这些型号的复印纸的长、宽之比为 .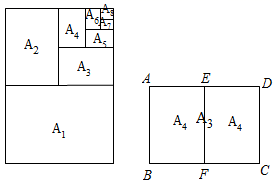
三、解答题
-
16.(1)、解方程:(2)、解方程:17. 如图,一次函数 与 轴交于点 ,与 轴交于点 ,与反比例函数 ( )交于点 ,且 .
 (1)、求出点 的坐标及反比例函数的关系表达式;(2)、请直接写出不等式 的解集.18. 如图是一个能自由转动的正五边形转盘,这个转盘被五条分割线分成形状相同,面积相等的五部分,且每个部分分别标有1、2、3、4、5五个数字,指针的位置固定不动,让转盘自由转动,当转盘停止后,记录指针指向的数(当指针指向分割线时,视其指向分割线左边的区域).
(1)、求出点 的坐标及反比例函数的关系表达式;(2)、请直接写出不等式 的解集.18. 如图是一个能自由转动的正五边形转盘,这个转盘被五条分割线分成形状相同,面积相等的五部分,且每个部分分别标有1、2、3、4、5五个数字,指针的位置固定不动,让转盘自由转动,当转盘停止后,记录指针指向的数(当指针指向分割线时,视其指向分割线左边的区域). (1)、若转动该转盘一次,则指针指向的数字为偶数的概率为;(2)、若连续转动转盘两次,请用“列表法”或“画树状图法”,求出两次指针指向的数字和为偶数的概率.19. 如图,在 中, ,以点 为圆心, 为半径的圆与 交于点 ,直线 与 相切,并且交 于点 ,与 的延长线交于点 .
(1)、若转动该转盘一次,则指针指向的数字为偶数的概率为;(2)、若连续转动转盘两次,请用“列表法”或“画树状图法”,求出两次指针指向的数字和为偶数的概率.19. 如图,在 中, ,以点 为圆心, 为半径的圆与 交于点 ,直线 与 相切,并且交 于点 ,与 的延长线交于点 . (1)、求证: ;(2)、若 , ,求 的长.20. 阅读下列材料,并完成相应的学习任务:
(1)、求证: ;(2)、若 , ,求 的长.20. 阅读下列材料,并完成相应的学习任务:图形旋转的应用.图形的旋转是全等变换(平移、轴对称、旋转)中重要的变换之一,利用图形旋转中的对应线段的长度、对应角的大小相等,旋转前后图形的大小和形状没有改变等性质,可以将一般图形转化成特殊图形,从而达到解决问题的目的.


如图,在 中, , 平分 ,且 , .过点 作互相垂直的两条直线,即 , 交 于点 , 交 于点 ,求四边形 的面积.
分析:将 以点 为旋转中心顺时针旋转,使得旋转后 的对应线段所在直线垂直于 ,并且交 于点 ,旋转后 的对应线段所在直线交 于点 .则容易证明四边形 为正方形.因为 , , ,所以 ,
所以 .
学习任务:
(1)、四边形 的面积等于;(2)、如图,在 中, :①作出 的外接圆 ;
②作 的平分线,与 交于点 .
要求:尺规作图,不写作法,但保留作图痕迹
(3)、在(2)的基础上,若 ,则四边形 的面积等于 .21. 2020年秋冬以来,由于全国大葱种植面积的减少与产量的减产,10月份到12月份,大葱的批发价格持续走高。10月份大葱的批发价格为5元/公斤,12月份大葱的批发价格涨到7.2元/公斤.(1)、求10月份到12月份大葱批发价格的月平均增长率;(2)、进入12月份以来,某农贸市场按照7.2元/公斤的批发价购进大葱进行销售,销售价格为10元/公斤,每天能销售大葱500公斤,为了扩大销售,增加盈利,最大限度让利于顾客,该农贸市场决定对大葱进行降价销售,根据市场调查发现,大葱的销售单价每降低0.1元,每天的销售量将增加40公斤,求当大葱的销售价格降低多少元时,该农贸市场每天销售大葱的利润为1640元?22. 综合与实践已知四边形 与 均为正方形.
 (1)、数学思考:
(1)、数学思考:如图1,当点 在 边上,点 在 边上时,线段 与 的数量关系是 , 位置关系是 .
(2)、在图1的基础上,将正方形 以点 为旋转中心,逆时针旋转角度 ,得到图2,则(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;拓展探索:
(3)、如图3,若点 , , 在同一直线上,且 ,则线段 长为 . (直接写出答案即可,不要求写过程).23. 综合与探究如图,抛物线 经过 , 两点,直线 与 轴交于点 .点 是直线 上方抛物线上的一个动点,过点 作 轴,垂足为 ,并且交直线 于点 .
 (1)、请直接写出抛物线与直线 的函数关系表达式;(2)、当 时,求出点 的坐标;(3)、是否存在点 , ?若存在,求出 的值;若不存在,请说明理由.
(1)、请直接写出抛物线与直线 的函数关系表达式;(2)、当 时,求出点 的坐标;(3)、是否存在点 , ?若存在,求出 的值;若不存在,请说明理由.