山西省晋城市高平市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-03-08 类型:期末考试
一、单选题
-
1. 式子 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、2. 如果△ABC中,sinA=cosB= , 则下列最确切的结论是( )A、△ABC是直角三角形 B、△ABC是等腰三角形 C、△ABC是等腰直角三角形 D、△ABC是锐角三角形3. 一元二次方程 的根是( )A、1 B、-1 C、1和0 D、-1和04. 将抛物线 向左平移3个单位,那么所得新抛物线的表达式是( )A、 B、 C、 D、5. 如图,已知 , , , ,则DE的长为( )
 A、2 B、4 C、3 D、6. 如图,在平面直角坐标系中,△ABC与△A1B1C1是以点P为位似中心的位似图形,且顶点都在格点上,则点P的坐标为( )
A、2 B、4 C、3 D、6. 如图,在平面直角坐标系中,△ABC与△A1B1C1是以点P为位似中心的位似图形,且顶点都在格点上,则点P的坐标为( ) A、(﹣4,﹣3) B、(﹣3,﹣4) C、(﹣3,﹣3) D、(﹣4,﹣4)7. 两个不透明的口袋中各有三个相同的小球,将每个口袋中的小球分别标号为1,2,3.从这两个口袋中分别摸出一个小球,则下列事件为随机事件的是( )A、两个小球的标号之和等于1 B、两个小球的标号之和等于6 C、两个小球的标号之和大于1 D、两个小球的标号之和大于68. 如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )
A、(﹣4,﹣3) B、(﹣3,﹣4) C、(﹣3,﹣3) D、(﹣4,﹣4)7. 两个不透明的口袋中各有三个相同的小球,将每个口袋中的小球分别标号为1,2,3.从这两个口袋中分别摸出一个小球,则下列事件为随机事件的是( )A、两个小球的标号之和等于1 B、两个小球的标号之和等于6 C、两个小球的标号之和大于1 D、两个小球的标号之和大于68. 如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )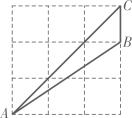 A、 B、 C、 D、9. 关于x的方程 (a为常数)的根的情况,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根一个负根 D、无实数根10. 如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3),若抛物线y=ax2的图象与正方形有公共顶点,则实数a的取值范围是( )
A、 B、 C、 D、9. 关于x的方程 (a为常数)的根的情况,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根一个负根 D、无实数根10. 如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3),若抛物线y=ax2的图象与正方形有公共顶点,则实数a的取值范围是( )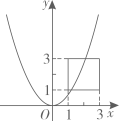 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. .12. 在 中,D、E分别是AB、AC的中点,若 面积为 ,则四边形DBCE的面积为 .
 13. 如图,在一块长12m,宽8m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条平行),剩余部分栽种花草,且栽种花草的面积77m²,设道路的宽为x m,则根据题意,可列方程为.
13. 如图,在一块长12m,宽8m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条平行),剩余部分栽种花草,且栽种花草的面积77m²,设道路的宽为x m,则根据题意,可列方程为.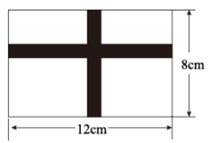 14. 抛物线 的部分图象如图所示,其与x轴的一个交点坐标为 ,对称轴为 ,则 时,x的取值范围 .
14. 抛物线 的部分图象如图所示,其与x轴的一个交点坐标为 ,对称轴为 ,则 时,x的取值范围 . 15. 如图,在矩形ABCD中,BD是对角线, ,垂足为E,连CE,若 ,则 .
15. 如图,在矩形ABCD中,BD是对角线, ,垂足为E,连CE,若 ,则 .
三、解答题
-
16.(1)、计算: ;(2)、用配方法解方程 .17. 关于x的方程 有实数根,且m为正整数,求m的值及此时方程的根.18. 阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则 = .下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…

任务:
(1)、请按照上面的证明思路,写出该证明的剩余部分;(2)、填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .19. 小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.(1)、小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)、若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.20. 云冈石窟位于大同市,位于第五窟的三世佛中央坐像是云冈石窟最大的佛像,某数学课题研究小组针对“三世佛中央坐像的高度有多少米”这一问题展开探究,过程如下:
问题提出:如图①是三世佛的中央坐像,请你设计方案并求出它的高度.
方案设计:如图②,该课题研究小组通过研究设计出以下方案,某同学在D处用测角器测得佛像最高处A的仰角 ,另一个同学在他的后方2.14m的E处测得佛像底端B的仰角 .
数据收集:通过查阅资料和实际测量:佛像底端到观景台的垂直距离BC为5m.
问题解决:
(1)、根据上述方案及数据,求佛像AB的高度;(结果保留整数,参考数据: , , , , , )(2)、如果你是课题小组的成员,你还有其它的测量方案吗?请说出你的测量方案和需要测量的数据?21. 在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量 (单位:件)与线下售价 (单位:元/件, )满足一次函数的关系,部分数据如下表:x(元/件)
12
13
14
15
16
y(件)
1200
1100
1000
900
800
(1)、求 与 的函数关系式;(2)、若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当 为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.22. 问题情景:在数学活动课上,同学们对等腰三角形进行探究.在 中, ,在 中, ,已知 ,直线BD,CE交于点F. (1)、观察猜想:如图①,当 线段BD与CE之间的数量关系是 , 的度数是 .(2)、合作交流:小华受上述问题启发,在图②的基础上( ),探究线段BD与CE之间的数量关系和 的度数,请你帮小华完成任务.(3)、类比探究:在小华探究的基础上,同学们又提出了新的问题,如图③,当 时, 时,线段DB与CE之间的数量关系是 , 的度数是 .23. 如图,抛物线 与x轴交于点 和点 ,与y轴交于点C,顶点为D,连接 与抛物线的对称轴l交于点E.
(1)、观察猜想:如图①,当 线段BD与CE之间的数量关系是 , 的度数是 .(2)、合作交流:小华受上述问题启发,在图②的基础上( ),探究线段BD与CE之间的数量关系和 的度数,请你帮小华完成任务.(3)、类比探究:在小华探究的基础上,同学们又提出了新的问题,如图③,当 时, 时,线段DB与CE之间的数量关系是 , 的度数是 .23. 如图,抛物线 与x轴交于点 和点 ,与y轴交于点C,顶点为D,连接 与抛物线的对称轴l交于点E.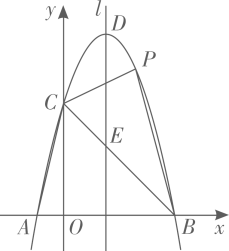 (1)、求抛物线的表达式;(2)、点P是第一象限内抛物线上的动点,连接 ,当 时,求点P的坐标;(3)、点N是对称轴l右侧抛物线上的动点,在射线 上是否存在点M,使得以点M,N,E为顶点的三角形与 相似?若存在,求点M的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、点P是第一象限内抛物线上的动点,连接 ,当 时,求点P的坐标;(3)、点N是对称轴l右侧抛物线上的动点,在射线 上是否存在点M,使得以点M,N,E为顶点的三角形与 相似?若存在,求点M的坐标;若不存在,请说明理由.