内蒙古自治区赤峰市宁城县2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-03-08 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列方程是一元二次方程的是（）

A、 $a x^{2} + b x + c = 0$ B、 $x^{2} - 2 = x (x - 1)$ C、 $3 x^{2} - 2 x + y = 5$ D、 $2 x^{2} + 1 = 0$

查看试题解析
3. 下列事件是随机事件的是（）

A、方程ax²+2x+1=0是一元二次方程 B、平行四边形是中心对称图形 C、直径是圆中最长的弦 D、二次函数y=-（x-1）²+3的最小值为3

查看试题解析
4. 若二次函数y=mx²-（m²-3m）x+1-m的图象关于y轴对称，则m的值为（）

A、0 B、3 C、1 D、0或3

查看试题解析
5. 如图，⊙O的半径为5，AB为弦，点C为 $\overset{⌢}{A B}$ 的中点，若∠ABC=30°，则弦AB的长为（　　）

A、 $\frac{1}{2}$ B、5 C、 $\frac{5 \sqrt{3}}{2}$ D、5 $\sqrt{3}$

查看试题解析
6. 如图，PA、PB是⊙O切线，A、B为切点，点C在⊙O上，且∠ACB＝55°，则∠APB等于（）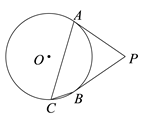

A、55° B、70° C、110° D、125°

查看试题解析

二、填空题

7. 关于x的一元二次方程（a﹣1）x²＋x＋a²﹣1＝0的一个根0，则a值为.

查看试题解析
8. 已知二次函数y=（m-3）x²的图象开口向下，则m的取值范围是

查看试题解析
9. 已知点 $p_{1} (a - 1, 1)$ 和 $p_{2} (2, b - 1)$ 关于原点对称，则a+b=.

查看试题解析
10. 在一个不透明袋子里有1个红球、1个黄球、n个白球，除颜色外其余都相同，每次摇匀后随机摸出一个小球，记下颜色后再放回袋中，经过大量重复摸球试验后发现摸到白球的频率稳定在0.5左右，则n的值为

查看试题解析
11. 已知圆锥的底面半径为20，侧面积为600π，则这个圆锥的母线长为.

查看试题解析
12. 现准备开展教职工排球比赛，赛制为单循环形式（每两队之间赛一场），若安排21场比赛，设x个球队参赛，根据题意，可列方程为

查看试题解析
13. 如图，A、B为抛物线y＝x²上的两点，且AB//x轴，与y轴交于点C，以点O为圆心，OC为半径画圆，若AB＝2 $\sqrt{2}$ ，则图中阴影部分的面积为

查看试题解析
14. 如图，抛物线y=（x-1）²-1与直线y=x交于点O，点B为线段OA上的动点，过点B作BC∥y轴，交交抛物线于点C，则线段BC长度的最大值为

查看试题解析

三、解答题

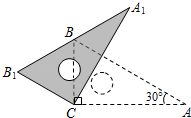
15. 用配方法解方程2x²-6x+1=0

查看试题解析
16. 已知关于x的一元二次方程方程（k-1）x²+2x-2=0有两个不相等的实数根求整数k的最小值

查看试题解析
17. 甲、乙、丙、丁四个人玩“击鼓传花”的游戏，游戏规则是第一次由甲将花随机传给乙、丙、丁三人中的某一人，以后的每一次都是由接到花的人随机传给其他三人中的某一人

(1)、甲第一次传花时，恰好传给乙的概率是

(2)、请用画树状图或列表的方法求经过两次传花后，花恰好回到甲手中的概率

查看试题解析
18. 如图，在三角板ABC中，∠ACB＝90°，∠A＝30°，AC＝6，将三角板ABC绕点C逆时针旋转，当起始位置时的点B恰好落在边A₁B₁上时，求A₁B的长

查看试题解析
19. 如图，△ABC在平面直角坐标系中，顶点的坐标分别为A(-4，4)，B(-1，1)，C(-1，4)．

(1)、画出与△ABC关于y轴对称的△A₁B₁C₁ ．

(2)、将△ABC绕点B逆时针旋转90°，得到△A₂BC₂ ，画两出△A₂BC₂ ．

(3)、求线段AB在旋转过程中扫过的图形面积．(结果保留π)

查看试题解析
20. 如图，抛物线y₁＝a（x﹣1）²+4与x轴交于A（﹣1，0）．

(1)、求该抛物线所表示的二次函数的表达式；

(2)、一次函数y₂＝x+1的图象与抛物线相交于A ， C两点，过点C作CB垂直于x轴于点B ，求△ABC的面积．

查看试题解析
21. 疫情复学后学校为每个班级买了免洗抑菌洗手液，当购买量不超过100瓶时，洗手液的单价为8元；超过100瓶时，每增加10瓶，每瓶单价就降低0.2元，但最低价格不低于每瓶5元，设学校共买了x瓶洗手液

(1)、当x=80时，每瓶洗手液的价格是元；当x=150时，每瓶洗手液的价格是元；当x=时，每瓶洗手液的价格恰好降为5元

(2)、若学校共花费1200元，请问一共购买了多少瓶洗手液？

查看试题解析
22. 如图，在Rt△ABC中，∠ACB＝90°，D为AB的中点，以CD为直径的⊙O交BC于点E ，过点E作EF⊥AB于点F ．

(1)、判断EF所在直线与⊙O的位置关系，并说明理由．

(2)、若∠B＝40°，⊙O的半径为6，求 $\overset{⌢}{E C}$ 的长．（结果保留π）

查看试题解析
23. 如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点，且BM＝CN，连接OM、ON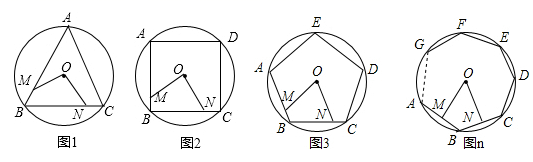

(1)、求图1中∠MON的度数

(2)、图2中∠MON的度数是，图3中∠MON的度数是

(3)、试探究∠MON的度数与正n边形边数n的关系是

查看试题解析
24. 某工厂生产一种产品，每件成本价16元，批发单价y（元）与一次性批发量x（件）（x为正整数）之间满足如图所示的函数关系

(1)、请直接写出y与x之间满足的函数关系式，并写出自变量x的取值范围

(2)、若一次性批发量不超过60件，当批发量为多少件时，工厂获利最大？最大利润是多少？

查看试题解析
25. 如图，在平面直角坐标系中，直线 $y = - x + 4$ 与x轴、y轴分别交于点A、点B，抛物线 $y = - \frac{1}{3} {(x - m)}^{2} + n$ 的顶点P在直线 $y = - x + 4$ 上，抛物线与y轴交于点C（点P、C不与点B重合），以BC为边作矩形BCDE，且CD＝2，点P、D在y轴的同侧

(1)、写出n＝；点C的纵坐标是（都用含m的代数式表示）

(2)、当P在第一象限且在矩形BCDE的边DE上时，求抛物线对应的函数表达式

(3)、设矩形BCDE的周长为d（d＞0），求d与m之间的函数表达式

查看试题解析
26. 如图，在△ABC中，AC＝BC＝4，∠ACB＝90°，动点P从点A出发，沿AB以每秒 $\frac{\sqrt{2}}{2}$ 个单位长度的速度向点B运动，点Q从点A出发，沿折线AC﹣CB向点B以每秒2个单位长度的速度运动，过点P作AC的平行线与过点Q作AB的平行线交于点D，当有一个点到达终点时，另一个点也停止运动，设△PQD与△ABC重叠部分图形的面积为S，运动的时间为t（秒）

(1)、点P到AC的距离为（用含t的代数式表示）

(2)、当点D落在BC上时，求t的值

(3)、当△PQD与△ABC重叠部分图形是三角形时，求S与t的函数关系式（S＞0）

查看试题解析