内蒙古自治区包头市青山区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-03-08 类型:期末考试
一、单选题
-
1. 反比例 的图象经过点(-1,3),则k的值为( )A、3 B、 C、 D、-32. 下列式子正确的是( )A、 B、 C、 D、3. 如图是由若干个完全相同的小正方体组合而成的几何体,若将小正方体①移动到小正方体②的正上方,下列关于移动后几何体的三视图说法正确的是( )
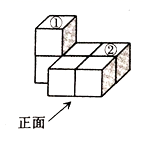 A、左视图发生变化 B、俯视图发生变化 C、主视图发生改变 D、左视图、俯视图和主视图都发生改变4. 已知水库的拦水坝斜坡的坡度为 ,则这个拦水坝的坡角为( )度.A、30 B、45 C、60 D、905. 关于x的一元二次方程 的两根分别为 , ,下列判断一定正确的是( )A、a=-1 B、c=1 C、ac=-1 D、6. 如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5m,点F到地面的高度FC=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度GA为( )
A、左视图发生变化 B、俯视图发生变化 C、主视图发生改变 D、左视图、俯视图和主视图都发生改变4. 已知水库的拦水坝斜坡的坡度为 ,则这个拦水坝的坡角为( )度.A、30 B、45 C、60 D、905. 关于x的一元二次方程 的两根分别为 , ,下列判断一定正确的是( )A、a=-1 B、c=1 C、ac=-1 D、6. 如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5m,点F到地面的高度FC=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度GA为( ) A、1.2m B、1.3m C、1.4m D、1.5m7. 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如表的表格,则符合这一结果的实验最有可能的是( )
A、1.2m B、1.3m C、1.4m D、1.5m7. 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如表的表格,则符合这一结果的实验最有可能的是( )实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A、抛一枚硬币,出现正面 B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、抛一个质地均匀的正六面体骰子(六个面上分别标1,2,3,4,5,6),向上的面点数是5 D、从一个装有2个白球和1个红球的袋子中任取一球,取到红球8. 已知∠PAQ=36°,点B为射线AQ上一固定点,按以下步骤作图:①分别以A,B为圆心,大于 AB的长为半径画弧,相交于两点M,N;②作直线MN交射线AP 于点D,连接 BD;③以B为圆心,BA长为半径画弧,交射线AP 于点C; 根据以上作图过程及所作图形,下列结论中错误的是( )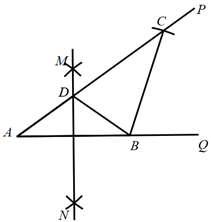 A、∠CDB=72°
A、∠CDB=72° B、△ADB∽△ABC
C、CD:AD=2:1
D、∠ABC=3∠ACB
9. 现有下列命题:
B、△ADB∽△ABC
C、CD:AD=2:1
D、∠ABC=3∠ACB
9. 现有下列命题:①若 ,则一元二次方程 有实数根;②有两条边长比值是 的两个直角三角形相似;③有一条对角线平分一组对角的四边形是菱形;④若点 , 在反比例函数 的图象上,且 ,则a的取值范围是 .
其中真命题的个数为( )
A、3个 B、2个 C、1个 D、0个10. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于F,连接DF,若BF= ,BC=3 ,则DF=( ) A、4 B、3 C、2 D、11. 如图,直线 与双曲线 交于 , ,直线AB交x轴于 ,下列命题:① ;②当 时, ;③若 为线段AB的中点,则 ,其中正确的命题有( )
A、4 B、3 C、2 D、11. 如图,直线 与双曲线 交于 , ,直线AB交x轴于 ,下列命题:① ;②当 时, ;③若 为线段AB的中点,则 ,其中正确的命题有( ) A、①② B、②③ C、①③ D、①②③12. 如图,在矩形OABC中, , ,把矩形OABC绕点A旋转,得到矩形ADEF且点D恰好落在BC上,连接OF交AD于点G.则点G的坐标是( )
A、①② B、②③ C、①③ D、①②③12. 如图,在矩形OABC中, , ,把矩形OABC绕点A旋转,得到矩形ADEF且点D恰好落在BC上,连接OF交AD于点G.则点G的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 在 中,若 ,则 的度数为 .14. 关于x的方程 有实数根,其中k为非正整数,则满足条件的k的代数和为 .15. 一个几何体的三视图如图所示,其中从上面看的视图是一个等边三角形,则这个几何体的表面积为 .
 16. 如图,点 在钝角 的边 上,连接 , , , ,则 的余弦值为 .
16. 如图,点 在钝角 的边 上,连接 , , , ,则 的余弦值为 . 17. 如图,在平面直角坐标系中,点 , 的坐标分别为 , ,点 是反比例函数 图象上一点, , 交 轴于点 , ,则 的值为 .
17. 如图,在平面直角坐标系中,点 , 的坐标分别为 , ,点 是反比例函数 图象上一点, , 交 轴于点 , ,则 的值为 . 18. 如图,在 中, ,点 在 边上, ,点 在AC上, ,垂足为 ,若 , ,则线段 的长为 .
18. 如图,在 中, ,点 在 边上, ,点 在AC上, ,垂足为 ,若 , ,则线段 的长为 . 19. 如图,在 中, ,在 的外部和内部(不包括边)分别取点 , ,若 , , , 补角等于 ,则下列结论:①点 在线段 的垂直平分线上;② ;③ ;④ 的最大值是 .其中正确的结论是 . (填写所有正确结论的序号)
19. 如图,在 中, ,在 的外部和内部(不包括边)分别取点 , ,若 , , , 补角等于 ,则下列结论:①点 在线段 的垂直平分线上;② ;③ ;④ 的最大值是 .其中正确的结论是 . (填写所有正确结论的序号)
三、解答题
-
20. 一个不透明的口袋中装有4个除颜色外,其他都一样的小球,其中有2个黄球,2个蓝球,现从中随机摸出2个球,则这2个球为同色的概率是 .21. 某校为了了解全校学生线上学习情况,随机选取该校部分学生,调查学生居家学习时每天学习时间(包括线上听课及完成作业时间).以下是根据调查结果绘制的统计图表.请你根据图表中的信息完成下列问题:
频数分布表
学习时间分组
频数
频率
A组( )
9
m
B组( )
18
0.3
C组( )
18
0.3
D组( )
n
0.2
E组( )
3
0.05
 (1)、频数分布表中 , , 并将频数分布直方图补充完整;(2)、若该校有学生1000名,现要对每天学习时间低于2小时的学生进行提醒,根据调查结果,估计全校需要提醒的学生有多少名?(3)、已知调查的E组学生中有2名男生1名女生,老师随机从中选取2名学生进一步了解学生居家学习情况.请用树状图或列表求所选2名学生恰为一男生一女生的概率.22. 为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东30°方向,C在A的南偏西15°方向 处.学生分成两组,第一组前往A地,第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是 ,第二组乘公交车,速度是 ,两组同学到达目的地分别用了多长时间?哪组同学先到达目的地?请说明理由(结果保留根号)
(1)、频数分布表中 , , 并将频数分布直方图补充完整;(2)、若该校有学生1000名,现要对每天学习时间低于2小时的学生进行提醒,根据调查结果,估计全校需要提醒的学生有多少名?(3)、已知调查的E组学生中有2名男生1名女生,老师随机从中选取2名学生进一步了解学生居家学习情况.请用树状图或列表求所选2名学生恰为一男生一女生的概率.22. 为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东30°方向,C在A的南偏西15°方向 处.学生分成两组,第一组前往A地,第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是 ,第二组乘公交车,速度是 ,两组同学到达目的地分别用了多长时间?哪组同学先到达目的地?请说明理由(结果保留根号)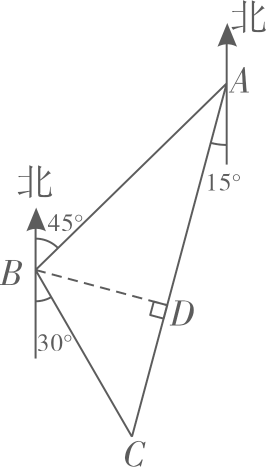 23. 如图,在 中, 于点O,交 于点E, 交 于点F,连接 ,点H为线段 上一点,连接 、 .
23. 如图,在 中, 于点O,交 于点E, 交 于点F,连接 ,点H为线段 上一点,连接 、 . (1)、判断四边形 的形状,并说明理由.(2)、当 时,求证: .24. 资料:公司营销区域面积是指公司营销活动范围内的地方面积,公共营销区域面积是指两家及以上公司营销活动重叠范围内的地方面积.
(1)、判断四边形 的形状,并说明理由.(2)、当 时,求证: .24. 资料:公司营销区域面积是指公司营销活动范围内的地方面积,公共营销区域面积是指两家及以上公司营销活动重叠范围内的地方面积.材料:某地有A,B两家商贸公司(以下简称A,B公司).去年下半年A,B公司营销区域面积分别为m平方千米,n平方千米,其中 ,公共营销区域面积与A公司营销区域面积的比为 ;今年上半年,受政策鼓励,各公司决策调整,A公司营销区域面积比去年下半年增长了 ,B公司营销区域面积比去年下半年增长的百分数是A公司的4倍,公共营销区域面积与A公司营销区域面积的比为 ,同时公共营销区域面积与A,B两公司总营销区域面积的比比去年下半年增加了x个百分点.
问题:
(1)、根据上述材料,针对去年下半年,提出一个你喜欢的数学问题(如求去年下半年公共营销区域面积与B公司营销区域面积的比),并解答;(2)、若同一个公司去年下半年和今年上半年每平方千米产生的经济收益持平,且A公司每半年每平方千米产生的经济收益均为B公司的1.5倍,求去年下半年与今年上半年两公司总经济收益之比.25. 已知矩形 中, , . (1)、如图 ,点 从点 开始沿 以每秒1个单位的速度移动,同时另一个点 从点 开始在线段 上以每秒3个单位的速度往返移动.设 , 运动时间为 秒,当 时,是否存在这样的时刻,四边形 为平行四边形?若存在,请求出 的值;若不存在,请说明理由;(2)、如图2,将矩形 折叠,使点 与点 重合,点 与点 重合,展平后折痕为 ,一动点 从点 出发,沿 ,以每秒1个单位的速度移动一周,设 运动的时间为 秒,请直接写出当 为直角三角形时 的值.26. 如图,矩形OABC的顶点A , C分别落在x轴,y轴的正半轴上,顶点B(2,2 ),反比例函数 (x 0)的图象与BC , AB分别交于D , E , BD= .
(1)、如图 ,点 从点 开始沿 以每秒1个单位的速度移动,同时另一个点 从点 开始在线段 上以每秒3个单位的速度往返移动.设 , 运动时间为 秒,当 时,是否存在这样的时刻,四边形 为平行四边形?若存在,请求出 的值;若不存在,请说明理由;(2)、如图2,将矩形 折叠,使点 与点 重合,点 与点 重合,展平后折痕为 ,一动点 从点 出发,沿 ,以每秒1个单位的速度移动一周,设 运动的时间为 秒,请直接写出当 为直角三角形时 的值.26. 如图,矩形OABC的顶点A , C分别落在x轴,y轴的正半轴上,顶点B(2,2 ),反比例函数 (x 0)的图象与BC , AB分别交于D , E , BD= . (1)、求反比例函数关系式和点E的坐标;(2)、写出DE与AC的位置关系并说明理由;(3)、点F在直线AC上,点G是坐标系内点,当四边形BCFG为菱形时,求出点G的坐标并判断点G是否在反比例函数图象上.
(1)、求反比例函数关系式和点E的坐标;(2)、写出DE与AC的位置关系并说明理由;(3)、点F在直线AC上,点G是坐标系内点,当四边形BCFG为菱形时,求出点G的坐标并判断点G是否在反比例函数图象上.