河北省唐山市滦南县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-03-08 类型:期末考试
一、单选题
-
1. 一元二次方程x(x﹣2)=x﹣2的解是( )A、x1=x2=0 B、x1=x2=1 C、x1=0,x2=2 D、x1=1,x2=22. 若 ,且 ,则 的值是( )A、4 B、2 C、20 D、143. 某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,这一问题中样本是( )A、100 B、被抽取的100名学生家长 C、被抽取的100名学生家长的意见 D、全校学生家长的意见4. 反比例函数y=(a-1)xa 的图象在 ( )A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限5. 如图, 为 的直径,C,D为 上两点,若 ,则 等于( )
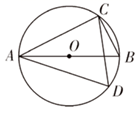 A、35° B、55° C、65° D、70°6. 关于x的方程 ( 为常数)根的情况下,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根,一个负根 D、无实数根7. “红色小讲解员”演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,这两组数据一定不变的是( ).A、中位数 B、众数 C、平均数 D、方差8. 下列对二次函数 的图像的描述,正确的是( )A、开口向下 B、对称轴是y轴 C、顶点坐标为 D、在对称轴右侧部分,y随x的增大而减小9. 如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',以下说法中错误的是( )
A、35° B、55° C、65° D、70°6. 关于x的方程 ( 为常数)根的情况下,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根,一个负根 D、无实数根7. “红色小讲解员”演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,这两组数据一定不变的是( ).A、中位数 B、众数 C、平均数 D、方差8. 下列对二次函数 的图像的描述,正确的是( )A、开口向下 B、对称轴是y轴 C、顶点坐标为 D、在对称轴右侧部分,y随x的增大而减小9. 如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',以下说法中错误的是( )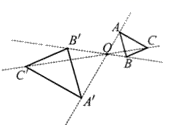 A、△ABC∽△A'B'C' B、点C,点O,点C'三点在同一直线上 C、AO:AA'=1∶2 D、AB∥A'B'10. 如图,撬钉子的工具是一个杠杆,动力臂 ,阻力臂 ,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是( )
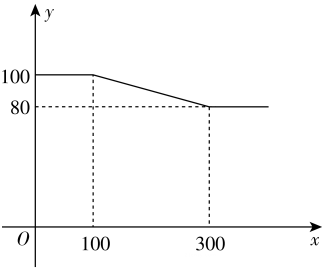
A、△ABC∽△A'B'C' B、点C,点O,点C'三点在同一直线上 C、AO:AA'=1∶2 D、AB∥A'B'10. 如图,撬钉子的工具是一个杠杆,动力臂 ,阻力臂 ,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是( )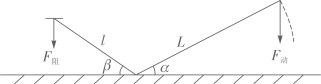 A、越来越小 B、不变 C、越来越大 D、无法确定11. 把一元二次方程 化成 的形式,则 的值( )A、3 B、5 C、6 D、812. 为节约用电,某市根据每户居民每月用电量分为三档收费.
A、越来越小 B、不变 C、越来越大 D、无法确定11. 把一元二次方程 化成 的形式,则 的值( )A、3 B、5 C、6 D、812. 为节约用电,某市根据每户居民每月用电量分为三档收费.第一档电价:每月用电量低于240度,每度0.4883元;
第二档电价:每月用电量为240~400度,每度0.5383元;
第三档电价:每月用电量高于400度,每度0.7883元.
小灿同学对该市有1000户居民的某小区居民月用电量(单位:度)进行了抽样调查,绘制了如图所示的统计图.下列说法不合理的是( )
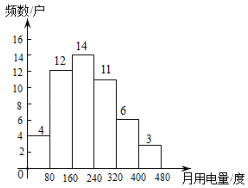 A、本次抽样调查的样本容量为50 B、该小区按第二档电价交费的居民有17户 C、估计该小区按第一档电价交费的居民户数最多 D、该小区按第三档电价交费的居民比例约为6%13. 如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D。下列结论不一定成立的是( )
A、本次抽样调查的样本容量为50 B、该小区按第二档电价交费的居民有17户 C、估计该小区按第一档电价交费的居民户数最多 D、该小区按第三档电价交费的居民比例约为6%13. 如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D。下列结论不一定成立的是( )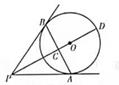 A、△BPA为等腰三角形 B、AB与PD相互垂直平分 C、点A,B都在以PO为直径的圆上 D、PC为△BPA的边AB上的中线14. 如图,正方形 的边长为4,以点A为圆心, 为半径画圆弧 得到扇形 (阴影部分,点E在对角线 上).若扇形 正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A、△BPA为等腰三角形 B、AB与PD相互垂直平分 C、点A,B都在以PO为直径的圆上 D、PC为△BPA的边AB上的中线14. 如图,正方形 的边长为4,以点A为圆心, 为半径画圆弧 得到扇形 (阴影部分,点E在对角线 上).若扇形 正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( ) A、 B、1 C、 D、15. 如图所示的4个三角形中,相似三角形有( )
A、 B、1 C、 D、15. 如图所示的4个三角形中,相似三角形有( )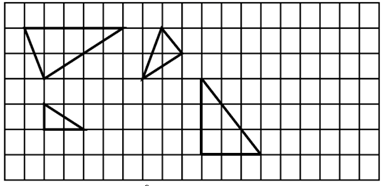 A、1对 B、2对 C、3对 D、4对16. 二次函数y=ax2十bx+c(a,b,c为常数,a≠0)的部分图象如图所示,图象顶点的坐标为(2,1),与x轴的一个交点在点(3,0)和点(4,0)之间,有下列结论:① ;② ;③c-4a=1;④ ;⑤ (m为任意实数).其中正确的有( )
A、1对 B、2对 C、3对 D、4对16. 二次函数y=ax2十bx+c(a,b,c为常数,a≠0)的部分图象如图所示,图象顶点的坐标为(2,1),与x轴的一个交点在点(3,0)和点(4,0)之间,有下列结论:① ;② ;③c-4a=1;④ ;⑤ (m为任意实数).其中正确的有( )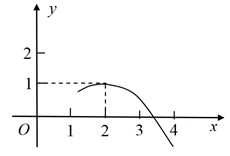 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
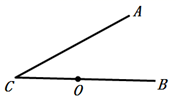
17. 如图, ,点 是 上的一点,且 ,则以4为半径的 与直线 的公共点的个数 .
 18. 若实数 , 满足 , ,则 的值为 .19. 如图,n个腰长为1的等腰直角三角形( ……)有一条腰在同一直线上,设 的面积为 , 的面积为 , 的面积为 ,……,则:
18. 若实数 , 满足 , ,则 的值为 .19. 如图,n个腰长为1的等腰直角三角形( ……)有一条腰在同一直线上,设 的面积为 , 的面积为 , 的面积为 ,……,则: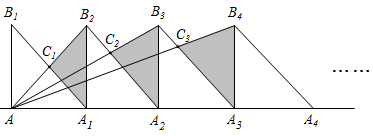 (1)、 ;(2)、 . (用含n的代数式表示)
(1)、 ;(2)、 . (用含n的代数式表示)三、解答题
-
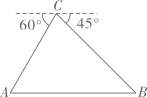
20. 关于x的一元二次方程x2+(2m+1)x+m2-1=0有两个不相等的实数根.(1)、求m的取值范围;(2)、写出一个满足条件的m的值,并求此时方程的根.21. 某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥 是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥 的上方120米的点C处悬停,此时测得桥两端A,B两点的俯角分别为60°和45°,求桥 的长度.
 22. 某公司销售部有营业员15人,该公司为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励,为了确定一个适当的月销售目标,公司有关部门统计了这15人某月的销售量,如下表所示:
22. 某公司销售部有营业员15人,该公司为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励,为了确定一个适当的月销售目标,公司有关部门统计了这15人某月的销售量,如下表所示:月销售量/件数
1770
480
220
180
120
90
人数
1
1
3
3
3
4
(1)、直接写出这15名营业员该月销售量数据的平均数、中位数、众数;(2)、如果想让一半左右的营业员都能达到月销售目标,你认为(1)中的平均数、中位数、众数中,哪个最适合作为月销售目标?请说明理由.温馨提示:确定一个适当的月销售目标是一个关键问题;如果目标定得太高,多数营业员完不成任务,会使营业员失去信心;如果目标定得太低,不能发挥营业员的潜力.
23. 从三角形(不是等腰三角形)一个顶点引一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线 . (1)、如图1,在 中, , 是 的完美分割线,且 ,求 的度数.(2)、如图2,在 中, , , 是 的完美分割线,且 是以 为底边的等腰三角形,找出 与 的关系.24. 如图,在平面直角坐标系 中,点 在反比例函数 的图象上,点 在 的延长线上, 轴,垂足为 , 与反比例函数的图象相交于点 ,连接 , .
(1)、如图1,在 中, , 是 的完美分割线,且 ,求 的度数.(2)、如图2,在 中, , , 是 的完美分割线,且 是以 为底边的等腰三角形,找出 与 的关系.24. 如图,在平面直角坐标系 中,点 在反比例函数 的图象上,点 在 的延长线上, 轴,垂足为 , 与反比例函数的图象相交于点 ,连接 , .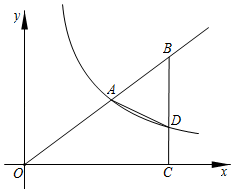 (1)、求该反比例函数的解析式;(2)、若 ,设点 的坐标为 ,求线段 的长.
(1)、求该反比例函数的解析式;(2)、若 ,设点 的坐标为 ,求线段 的长.