河北省唐山市路南区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-03-08 类型:期末考试
一、单选题
-
1. 反比例函数 的图象所在象限为( )A、一 B、二 C、一、三 D、二、四2. 下列光线所形成投影是平行投影的是( )A、太阳光线 B、台灯的光线 C、手电筒的光线 D、路灯的光线3. 抛物线 的对称轴为( )A、 轴 B、 轴 C、 D、4. 下列成语描述的事件为必然事件的是( )A、守株待兔 B、瓮中捉鳖 C、一步登天 D、拔苗助长5. 由 ,可得比例式( )A、 B、 C、 D、6. 如图是某一几何体的三视图,则该几何体是( )
 A、三棱柱 B、长方体 C、圆柱 D、圆锥7. 若点 在抛物线 上,则m的值为( )A、2 B、-2或1 C、2或-1 D、-18. 直线a上有一点到圆心O的距离等于⊙O的半径,则直线a与⊙O的位置关系是( )A、相离 B、相切 C、相交 D、相切或相交9. 如图,从点 观测建筑物 的视角是( )
A、三棱柱 B、长方体 C、圆柱 D、圆锥7. 若点 在抛物线 上,则m的值为( )A、2 B、-2或1 C、2或-1 D、-18. 直线a上有一点到圆心O的距离等于⊙O的半径,则直线a与⊙O的位置关系是( )A、相离 B、相切 C、相交 D、相切或相交9. 如图,从点 观测建筑物 的视角是( ) A、 B、 C、 D、10. 对于反比例函数 ,下列说法正确的是( )A、图象经过点 B、已知点 和点 ,则 C、其图象既是轴对称图形也是中心对称图形 D、当 时, 随 的增大而减小11. 如图,点I为 的内心, , , ,将 平移使其顶点与I重合,则图中阴影部分的周长为( )
A、 B、 C、 D、10. 对于反比例函数 ,下列说法正确的是( )A、图象经过点 B、已知点 和点 ,则 C、其图象既是轴对称图形也是中心对称图形 D、当 时, 随 的增大而减小11. 如图,点I为 的内心, , , ,将 平移使其顶点与I重合,则图中阴影部分的周长为( ) A、6 B、4 C、3 D、6.512. 若 的每条边长增加各自的 得 ,则 的度数与其对应角 的度数相比( )A、增加了 B、减少了 C、增加了 D、没有改变13. 正多边形的内切圆与外接圆的半径之比为 ,则这个正多边形为( )A、正十二边形 B、正六边形 C、正四边形 D、正三角形14. 如图,下列条件使△ACD∽△ABC成立的是( )
A、6 B、4 C、3 D、6.512. 若 的每条边长增加各自的 得 ,则 的度数与其对应角 的度数相比( )A、增加了 B、减少了 C、增加了 D、没有改变13. 正多边形的内切圆与外接圆的半径之比为 ,则这个正多边形为( )A、正十二边形 B、正六边形 C、正四边形 D、正三角形14. 如图,下列条件使△ACD∽△ABC成立的是( ) A、 B、 C、AC2=AD·AB D、CD2=AD·BD15. 小明在解二次函数 时,只抄对了 , ,求得图象过点 .他核对时,发现所抄的 比原来的 值大2.则抛物线与 轴交点的情况是( )A、只有一个交点 B、有两个交点 C、没有交点 D、不确定
A、 B、 C、AC2=AD·AB D、CD2=AD·BD15. 小明在解二次函数 时,只抄对了 , ,求得图象过点 .他核对时,发现所抄的 比原来的 值大2.则抛物线与 轴交点的情况是( )A、只有一个交点 B、有两个交点 C、没有交点 D、不确定二、填空题
-
16. 两地的实际距离是 ,在地图上量得这两地的距离为 ,则这幅地图的比例尺为 .17. 举出一个生活中应用反比例函数的例子: .18. 一位篮球运动员在距离篮圈中心水平距离 处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为 时,达到最大高度 ,然后准确落入篮筐内.已知篮圈中心距离地面高度为 ,在如图所示的平面直角坐标系中,则此抛物线的解析式为 .

三、解答题
-
19.(1)、计算: .(2)、已知 是关于 的一元二次方程,求 的值.20. 如图,在平面直角坐标系中,点 , 的坐标分别是 , .
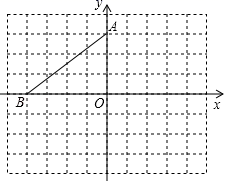 (1)、将 绕点 逆时针旋转90°得到 ,点 , 对应点分别是 , ,请在图中画出 ,并写出 的坐标;(2)、以 点为位似中心,将 作位似变换且缩小为原来的 ,在网格内画出一个符合条件的 .21. 如图在平面直角坐标系中, 点的坐标为 , 轴于点 , ,反比例函数 的图象的一支经过 的中点 ,且与 交于点 .
(1)、将 绕点 逆时针旋转90°得到 ,点 , 对应点分别是 , ,请在图中画出 ,并写出 的坐标;(2)、以 点为位似中心,将 作位似变换且缩小为原来的 ,在网格内画出一个符合条件的 .21. 如图在平面直角坐标系中, 点的坐标为 , 轴于点 , ,反比例函数 的图象的一支经过 的中点 ,且与 交于点 .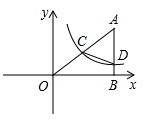 (1)、求反比例函数的解析式;(2)、求四边形 的面积.22. 三名运动员参加定点投篮比赛,原定甲、乙、丙依次出场.为保证公平竞争,现采用抽签方式重新确定出场顺序.(1)、画出抽签后每个运动员出场顺序的树状图;(2)、求:①抽签后甲运动员的出场顺序发生变化的概率;
(1)、求反比例函数的解析式;(2)、求四边形 的面积.22. 三名运动员参加定点投篮比赛,原定甲、乙、丙依次出场.为保证公平竞争,现采用抽签方式重新确定出场顺序.(1)、画出抽签后每个运动员出场顺序的树状图;(2)、求:①抽签后甲运动员的出场顺序发生变化的概率;②抽签后每个运动员的出场顺序都发生变化的概率.
23. 如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m. (1)、当吊臂底部A与货物的水平距离AC为5m时,求吊臂AB的长;(2)、如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计,计算结果精确到0.1m,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)24. 某单位为响应市“创建全国文明城市”的号召,不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过 ,另外三边由 长的栅栏围成.设矩形 空地中,垂直于墙的边 ,面积为 (如图).
(1)、当吊臂底部A与货物的水平距离AC为5m时,求吊臂AB的长;(2)、如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计,计算结果精确到0.1m,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)24. 某单位为响应市“创建全国文明城市”的号召,不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过 ,另外三边由 长的栅栏围成.设矩形 空地中,垂直于墙的边 ,面积为 (如图). (1)、求 与 之间的函数关系式,并求出自变量 的取值范围;(2)、若矩形空地的面积为 ,求 的值;(3)、当矩形 空地的面积最大时,利用的墙长是多少 ;并求此时的最大面积.25. 如图(图形不全),等边三角形 中, ,点 在直线 上,点 在直线 上,且 ,当 时,求 的长.
(1)、求 与 之间的函数关系式,并求出自变量 的取值范围;(2)、若矩形空地的面积为 ,求 的值;(3)、当矩形 空地的面积最大时,利用的墙长是多少 ;并求此时的最大面积.25. 如图(图形不全),等边三角形 中, ,点 在直线 上,点 在直线 上,且 ,当 时,求 的长.几位同学通过探究得出结论:此题有多种结果.有同学已经得出两个符合题意结论:①当点 在边 上、点 在边 上时, ;②当点 在边 上、点 在 的延长线上时, .
要求:请针对其它情况,继续求出 的长,并写出总的正确结论.
