河北省唐山市路北区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-03-08 类型:期末考试
一、单选题
-
1. 下列关系式中,y是x的反比例函数的是( )A、y=4x B、 =3 C、y=﹣ D、y=x2﹣12. 下列事件中为必然事件的是( )A、早晨的太阳从东方升起 B、打开电视机,正在播放新闻 C、随机掷一枚硬币,落地后正面朝上 D、下雨后,天空出现彩虹3. 方程2x2﹣8x﹣1=0的解的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、有一个实数根4. 已知 与 相似,且相似比为 ,则 与 的周长比为( )A、 B、 C、 D、5. 若反比例函数y= 图象经过点(5,-1),该函数图象在( )A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限6. 用配方法解一元二次方程 ,下列配方正确的是( )A、 B、 C、 D、7. 如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为 , , .让转盘自由转动,指针停止后落在黄色区域的概率是
 A、 B、 C、 D、8. 如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A、 B、 C、 D、8. 如图,⊙O是△ABC的内切圆,则点O是△ABC的( )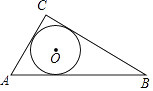 A、三条边的垂直平分线的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条高的交点9. 如图,AB是⊙O的直径,C,D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠BOC=( )
A、三条边的垂直平分线的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条高的交点9. 如图,AB是⊙O的直径,C,D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠BOC=( )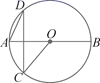 A、25° B、50° C、130° D、155°10. 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
A、25° B、50° C、130° D、155°10. 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( ) A、6 B、8 C、10 D、1211. 将抛物线y=3x2+2向左平移2个单位长度,再向下平移3个单位长度,则得到的抛物线的解析式为( )A、y=3(x﹣2)2﹣1 B、y=3(x﹣2)2+5 C、y=3(x+2)2﹣1 D、y=3(x+2)2+512.
A、6 B、8 C、10 D、1211. 将抛物线y=3x2+2向左平移2个单位长度,再向下平移3个单位长度,则得到的抛物线的解析式为( )A、y=3(x﹣2)2﹣1 B、y=3(x﹣2)2+5 C、y=3(x+2)2﹣1 D、y=3(x+2)2+512.如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
 A、逐渐增大 B、不变 C、逐渐减小 D、先增大后减小13. 如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中△ABC相似的是( )
A、逐渐增大 B、不变 C、逐渐减小 D、先增大后减小13. 如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中△ABC相似的是( ) A、
A、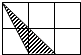 B、
B、 C、
C、 D、
D、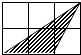 14. 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
14. 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )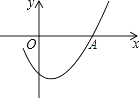 A、b2<4ac B、ac>0 C、2a﹣b=0 D、a﹣b+c=0
A、b2<4ac B、ac>0 C、2a﹣b=0 D、a﹣b+c=0二、填空题
-
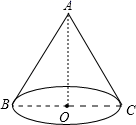
15. 已知⊙O的半径为 ,圆心O到直线L的距离为 ,则直线L与⊙O的位置关系是 .16. 若2是关于方程 的一个根,则这个方程的另一个根是 .17. 如图,圆锥的侧面积为15π,底面半径为3,则圆锥的高AO为 .
 18.
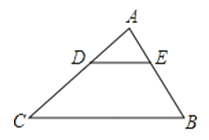
18.如图,在△ABC中,AB=9,AC=12,BC=18,D为AC上一点,DC=AC.在AB上取一点E得△ADE.若图中两个三角形相似,则DE的长是 .
三、解答题
-
19. 用适当的方法解下列方程:(1)、(2)、 .20. 已知反比函数 ,当x=2时,y=3.(1)、求m的值;(2)、当3≤x≤6时,求函数值y的取值范围.21. 如图,在平面直角坐标系中,已知 的三个顶点的坐标分别为 , , .
 (1)、若 以原点 为位似中心,缩小得到 ,相似比为 ,画出 ,并直接写出顶点 的坐标为;(2)、将 绕着点 按顺时针方向旋转90°得到 ,求出 点经过的路径长(不需画图).22. 如图,AD是⊙O的弦,AC是⊙O直径,⊙O的切线BD交AC的延长线于点B , 切点为D , ∠DAC=30°.
(1)、若 以原点 为位似中心,缩小得到 ,相似比为 ,画出 ,并直接写出顶点 的坐标为;(2)、将 绕着点 按顺时针方向旋转90°得到 ,求出 点经过的路径长(不需画图).22. 如图,AD是⊙O的弦,AC是⊙O直径,⊙O的切线BD交AC的延长线于点B , 切点为D , ∠DAC=30°.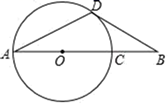 (1)、求证:△ADB是等腰三角形;(2)、若BC= ,求AD的长.23. 甲袋里装有红球5个,白球2个和黑球12个,乙袋里装有红球20个,白球20个和黑球10个.(1)、如果你想取出1个黑球,选哪个袋子成功的机会大?请说明理由.(2)、某同学说“从乙袋取出10个红球后,乙袋中的红球个数仍比甲袋中红球个数多,所以此时想取出1个红球,选乙袋成功的机会大.”你认为此说法符合题意吗?为什么?24. 如图,平行四边形ABCD放置在平面直角坐标系xOy中,已知A(-2,0),B(2,0),D(0,3),反比例函数y= (x>0)的图象经过点C.
(1)、求证:△ADB是等腰三角形;(2)、若BC= ,求AD的长.23. 甲袋里装有红球5个,白球2个和黑球12个,乙袋里装有红球20个,白球20个和黑球10个.(1)、如果你想取出1个黑球,选哪个袋子成功的机会大?请说明理由.(2)、某同学说“从乙袋取出10个红球后,乙袋中的红球个数仍比甲袋中红球个数多,所以此时想取出1个红球,选乙袋成功的机会大.”你认为此说法符合题意吗?为什么?24. 如图,平行四边形ABCD放置在平面直角坐标系xOy中,已知A(-2,0),B(2,0),D(0,3),反比例函数y= (x>0)的图象经过点C. (1)、求此反比例函数的解析式;(2)、问将平行四边形ABCD向上平移多少个单位,能使点B落在双曲线上?25. 小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.(1)、设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.(2)、当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?(3)、如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)26. 已知:如图,在矩形 中, , ,对角线 , 交于点 .点 从点 出发,沿 方向匀速运动,速度为 ;同时,点 从点 出发,沿 方向匀速运动,速度为 ;当一个点停止运动时,另一个点也停止运动.连接 并延点也长,交 于点 ,过点 作 ,交 于点 .设运动时间为 ,解答下列问题:
(1)、求此反比例函数的解析式;(2)、问将平行四边形ABCD向上平移多少个单位,能使点B落在双曲线上?25. 小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.(1)、设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.(2)、当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?(3)、如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)26. 已知:如图,在矩形 中, , ,对角线 , 交于点 .点 从点 出发,沿 方向匀速运动,速度为 ;同时,点 从点 出发,沿 方向匀速运动,速度为 ;当一个点停止运动时,另一个点也停止运动.连接 并延点也长,交 于点 ,过点 作 ,交 于点 .设运动时间为 ,解答下列问题: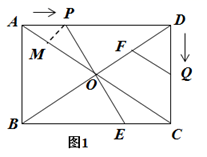 (1)、当t=2时, ;(2)、当t为何值时, 是等腰三角形?(3)、设五边形 的面积为 ,试确定 与 的函数关系式;(4)、在运动过程中,是否存在某一时刻 ,使 平分 ?若存在,直接写出 的值;若不存在,请说明理由.
(1)、当t=2时, ;(2)、当t为何值时, 是等腰三角形?(3)、设五边形 的面积为 ,试确定 与 的函数关系式;(4)、在运动过程中,是否存在某一时刻 ,使 平分 ?若存在,直接写出 的值;若不存在,请说明理由.