山西省长治市潞城区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-03-08 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各组数据中，是勾股数的是（）

A、3，4，5 B、1，2，3 C、8，9，10 D、5，6，9

查看试题解析
2. 已知数据： $\sqrt{3}$ ， $\sqrt{4}$ ， $- \sqrt{5}$ ，2π，0．其中无理数出现的频率为（）

A、0.2 B、0.4 C、0.6 D、0.8

查看试题解析
3. 下列运算正确的是（）

A、 $5 a b - a b = 4$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 ${(a^{2} b)}^{3} = a^{5} b^{3}$ D、 $a^{6} \div a^{2} = a^{4}$

查看试题解析
4. 下列命题中，是真命题的是（）

A、 $\sqrt{9}$ 的算术平方根是3 B、5是25的一个平方根 C、 ${(- 4)}^{2}$ 的平方根是-4 D、64的立方根是±4

查看试题解析
5. 如图，原来从A村到B村，需要沿路A→C→B（ $∠ C = 90 °$ ）绕过两地间的一片湖，在A ， B间建好桥后，就可直接从A村到B村．已知 $A C = 5 km$ ， $B C = 12 km$ ，那么，建好桥后从A村到B村比原来减少的路程为（）

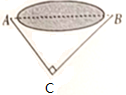A、2km B、4km C、10 km D、14 km

查看试题解析
6. 在 $△ A B C$ 中， $A B = B C$ ， $∠ A B C$ 的外角为 $80 °$ ，则 $∠ A$ 的度数（）

A、 $80 °$ B、 $50 °$ C、 $40 °$ D、 $20 °$

查看试题解析
7. 根据下列已知条件，不能判定 $△ A B C ≌ △ D E F$ 的是（）

A、 $A B = D E$ ， $B C = E F$ ， $A C = D F$ B、 $A B = D E$ ， $B C = E F$ ， $∠ A = ∠ C$ C、 $∠ A = ∠ D$ ， $∠ B = ∠ E$ ， $A B = D E$ D、 $A B = D E$ ， $B C = E F$ ， $∠ B = ∠ E$

查看试题解析
8. 如图，每个小正方形的边长都相等，A ， B ， C是小正方形的顶点，则 $∠ A B C$ 的度数为（）

A、 $45 °$ B、 $50 °$ C、 $55 °$ D、 $60 °$

查看试题解析
9. 2020年10月29日，中国共产党第十九届中央委员会第五次全体会议审议通过了《中共中央关于制定国民经济和社会发展第十四个五年规划和二O三五年远景目标的建议》，某校为了解全校1500名学生对十四五规划精神的认识，从中随机抽取了部分学生进行了“十四五精神学习效果”调查研究，把学习效果分成“优、良、中、差”四个等级，并进行统计，绘制了如图所示的两幅统计图，下列四个选项中错误的是（）

A、抽取了30名同学进行“十四五精神学习效果”调查 B、 $a = 84 °$ C、抽取的学生中，学习效果为“良”和“中”的总人数占抽取人数的55% D、调查发现，学习效果为“良”的人数最多

查看试题解析
10. 如图，透明的圆柱形玻璃容器（容器厚度忽略不计）的高为 $16 c m$ ，在容器内壁离容器底部 $4 c m$ 的点 $B$ 处有一滴蜂蜜，此时一只蚂蚁正好在容器外壁，位于离容器上沿 $4 c m$ 的点 $A$ 处，若蚂蚁吃到蜂蜜需爬行的最短路径为 $20 c m$ ，则该圆柱底面周长为（）

A、 $12 c m$ B、 $14 c m$ C、 $20 c m$ D、 $24 c m$

查看试题解析

二、填空题

11. 分解因式： $m^{2} + m =$ ．

查看试题解析
12. 某城市家庭人口数的次统计结果表明：两口之家占23%，三口人家占42%，四口之家占21%，五口之家占9%，六口之家占3%，其他占2%．若要制作统计图来反映这些数据，最适当的统计图是（从折线统计图、条形统计图、扇形统计图中选一个）．

查看试题解析
13. 如图，四边形ABCD中， $∠ B C D = 90 °$ ， $∠ A B D = ∠ D B C$ ， $A B = 5$ ， $D C = 6$ ，则 $△ A B D$ 的面积为．

查看试题解析
14. 如图所示的是学校行知苑中亭子的顶部，将其顶部抽象成一个三角形，在 $△ A B C$ 中，DE是AC的垂直平分线， $A C = 5$ 厘米， $△ A B D$ 的周长等于13厘米，则 $△ A B C$ 的周长是．

查看试题解析
15. 我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成个正方形和两对全等的直角三角形，得到一个恒等式，后人借助这种分割方法所得的图形证明了勾股定理，如图所示的图形就用了这种分割方法若 $A E = 5$ ，正方形ODCE的边长为1，则BD等于．

查看试题解析

三、解答题

16.

(1)、计算： $\sqrt[3]{- 27} + \sqrt{\frac{49}{64}} - {(- \frac{1}{2})}^{3}$

(2)、如图，四边形ABCD中，AB//DC ， DB平分 $∠ A D C$ ， $∠ A = 60 °$ ．求证： $△ A B D$ 是等边三角形．

查看试题解析
17. 先化简，再求值： $[{(x - y)}^{2} - (x - 2 y) (2 y + x)] \div (- y)$ ，其中 $x = - 1$ ， $y = 2$ ．

查看试题解析
18. 下面是小华同学分解因式 $9 a^{2} (x - y) + 4 b^{2} (y - x)$ 的过程，请认真阅读，并回答下列问题．
解：原式 $= 9 a^{2} (x - y) + 4 b^{2} (x - y)$ ①

$= (x - y) (9 a^{2} + 4 b^{2})$ ②

$= (x - y) {(3 a + 2 b)}^{2}$ ③

任务一：以上解答过程从第步开始出现错误．

任务二：请你写出正确的解答过程．

查看试题解析
19. “平地秋千为起，踏板一尺高地，送行二步与人齐，五尺人高曾记，仕女佳人争蹴，终朝笑语欢嬉，二公高士好争，算出索长有几？（注：二步=10尺）”这是商人出身的明代珠算大师程大位在他的部17卷的数学巨著《直指算法统宗》中用词的形式给出的一道题．这词生动地描绘了少女荡秋千的欢快场景，也是一道在当时颇有分量的数学题，你能解答这道题目吗？大意是“当秋千静止时，它的踏板离地的距离为1尺，将秋千的踏板往前推2步（这里的每1步合5尺），它的踏板与人一样高，这个人的身高为5尺，秋千的绳索始终是有这状态的，现在问：这个秋千的绳索有多长？”

查看试题解析
20. 如图，点E ， F在线段BD上，已知 $A F ⊥ B D$ ， $C E ⊥ B D$ ， $A D / / C B$ ， $D E = B F$ ，求证： $A F = C E$ ．

查看试题解析
21. 某校数学兴趣小组设计了“你最喜欢的放松方式”调查问卷（每人必选且只能选一种），在全校范围内随机调查了部分学生，并利用统计结果绘制了如下所示两幅不完整的统计图，请结合图中所给信息，解答下列问题：

(1)、本次调查问卷共调查了名学生，表示“其他”的扇形圆心角的度数是．

(2)、请你补充完整条形统计图．

(3)、从统计图中你能得出什么结论？说说你的想法．

查看试题解析

22. 综合与实践

读下列材料，完成文后任务．

小明在数学课外书上看到了这样一道题：如果x满足 $(6 - x) (x - 2) = 3$ ．求 ${(6 - x)}^{2} + {(x - 2)}^{2}$ 的值，怎么解决呢？小英给出了如下两种方法：

方法1：设 $6 - x = m$ ， $x - 2 = n$ ，则 $(6 - x) (x - 2) = m n = 3$ ， $m + n = 6 - x + x - 2 = 4$ ，

$∴ {(6 - x)}^{2} + {(x - 2)}^{2} = m^{2} + n^{2} = {(m + n)}^{2} - 2 m n = 4^{2} - 2 \times 3 = 16 - 6 = 10$

方法2： $∵ (6 - x) (x - 2) = 3$ ， $∴ 6 x - 12 + 2 x - x^{2} = 3$ ， $∴ x^{2} - 8 x = - 15$ ，

${(6 - x)}^{2} + {(x - 2)}^{2} = 36 - 12 x + x^{2} + x^{2} - 4 x + 4 = 2 x^{2} - 16 x + 40 = 2 (x^{2} - 8 x) + 40$

$= 2 \times (- 15) + 40 = - 30 + 40 = 10$ ．

任务

(1)、方法1用到的乘法公式是（填“平方差公式”或“完全平方公式”）．

(2)、请你用材料中两种方法中的一种解答问题：若

{(x - 11)}^{2} + {(9 - x)}^{2} = 10

，求

(x - 11) (9 - x)

的值．

(3)、如图，在长方形ABCD中，

A B = 10

，

B C = 6

，E ， F是BC ， CD上的点，且

B E = D F = x

，分别以FC ， CE为边在长方形ABCD外侧作正方形CFGH和 CEMN ，若长方形 CEPF的面积为40，求图中阴影部分的面积和．

查看试题解析

23. 综合与探究
在学习了轴对称变换后，我们经常会遇到三角形中的“折叠”问题，在解答这种问题时，通常会考虑到折叠前与折叠后的图形全等，并利用全等图形的性质，即对应角相等，对应边相等来研究解决数学中的“折叠”问题，每个小组剪了一些如图1所示的 $Rt △ A B C$ 纸片（ $∠ B = 90 °$ ， $A B = 6$ ， $B C = 8$ ）并进行探究：

(1)、如图2，“奋斗”小组将 $Rt △ A B C$ 纸片沿DE折叠，使点C落在 $△ A B C$ 外部的 $C'$ 处
①若 $∠ 1 = 40 °$ ， $∠ C = 37 °$ ，则 $∠ 2$ 的度数为．

② $∠ 1$ ， $∠ 2$ ， $∠ C$ 之间的数量关系为．

(2)、如图3，“勤奋”小组将 $△ A B C$ 沿DE折叠，使点C与点A重合，求BD的长；

(3)、如图4，“雄鹰”小组将 $△ A B C$ 沿AD折叠，使点B落在点E处，连接CE ，当 $△ C D E$ 为直角三角形时，求BD的长．

查看试题解析