山西省运城市万荣县2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-03-08 类型:期末考试
一、单选题
-
1. 4的平方根是( )A、2 B、16 C、±2 D、±2. 一个正方体的水晶砖,体积为 ,它的棱长大约在( )A、 之间 B、 之间 C、 之间 D、 之间3. 下列各组数中,以 为边的三角形不是直角三角形的是( )A、 B、 C、 D、4. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、5. 在一次“爱心捐助”捐款活动中,某班第一小组8名同学捐款的金额(单位:元)如表所示,则这 名同学捐款的平均金额为( )
金额/元
5
6
7
10
人数
2
3
2
1
A、6.5元 B、6元 C、3.5元 D、7元6. 已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )A、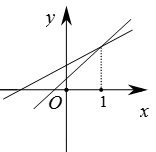 B、
B、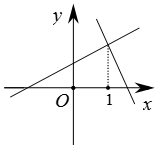 C、
C、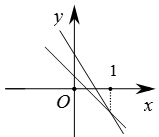 D、
D、 7. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容.
7. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容.已知:如图, .
求证: .
证明:延长BE交 ※ 于点F ,
则 ◎ (三角形的外角等于与它不相邻两个内角之和).
又 ,得 ▲ .
故 ( @ 相等,两直线平行).
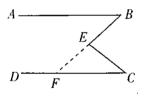
则回答正确的是( )
A、◎代表 B、@代表同位角 C、▲代表 D、※代表AB8. 《九章算术》中有这样一个题:今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其意思为:今有甲乙二人,不如其钱包里有多少钱,若乙把其一半的钱给甲,则甲的数为50;而甲把其 的钱给乙,则乙的钱数也为50,问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y,则可建立方程组为( )A、 B、 C、 D、9. 将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )。 A、45° B、60° C、75° D、85°10. 如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )
A、45° B、60° C、75° D、85°10. 如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )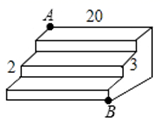 A、20dm B、25dm C、30dm D、35dm
A、20dm B、25dm C、30dm D、35dm二、填空题
-
11. 化简: .12. 在平面直角坐标系的第二象限内有一点 ,点 到 轴的距离为 ,到 轴的距离为 ,则点M的坐标是.13. 如图,以原点O为圆心, 为半径画弧与数轴交于点A,则点A在数轴上表示的数为.
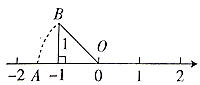 14. 在平面直角坐标系中,已知一次函数y=x-1的的图象经过 两点,若 ,则 (填“>”“<”或“=”)15. 如图,将一张长方形纸片 折叠成如图所示的形状, ,则 .
14. 在平面直角坐标系中,已知一次函数y=x-1的的图象经过 两点,若 ,则 (填“>”“<”或“=”)15. 如图,将一张长方形纸片 折叠成如图所示的形状, ,则 .
三、解答题
-
16. 计算题(1)、(2)、下面是小红同学解二元一次方程组的过程,请认真阅读并完成相应任务.
解:解方程组:
由②得, ▲ ③;……第一步
将③代入①,解得 ▲ ;……第二步
将 的值代入③,解得 ▲ ;……第三步
所以原方程组的解为 ▲ ……第四步
任务:①将上面的空格补充完整;
②本题解方程组的方法为 ▲ (填“代入消元法”或“加减消元法”)
17. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系后 的顶点均在格点上. (1)、作出 关于 轴对称的(2)、写出顶点 的坐标分别是 , ,(3)、求18. 如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D.
(1)、作出 关于 轴对称的(2)、写出顶点 的坐标分别是 , ,(3)、求18. 如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D. (1)、求证: ;(2)、若设△AEC三边分别为a、b、c,利用此图证明勾股定理.19. 第二十四届冬季奥林匹克运动会将于2022年2月4日至2月20日在北京举行,北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市.某区举办了一次冬奥知识网上答题竞赛,甲、乙两校各有400名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
(1)、求证: ;(2)、若设△AEC三边分别为a、b、c,利用此图证明勾股定理.19. 第二十四届冬季奥林匹克运动会将于2022年2月4日至2月20日在北京举行,北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市.某区举办了一次冬奥知识网上答题竞赛,甲、乙两校各有400名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.(收集数据)从甲、乙两校各随机抽取20名学生,在这次竞赛中他们的成绩如下:
甲
30
60
60
70
60
80
30
90
100
60
60
100
80
60
70
60
60
90
60
60
乙
80
90
40
60
80
80
90
40
80
50
80
70
70
70
70
60
80
50
80
80
(整理、描述数据)按如下分数段整理、描述这两组样本数据:
成绩
甲
2
14
4
(说明:优秀成绩为 ,良好成绩为 、合格成绩为 )
(1)、(分析数据)两组样本数据的平均分、中位数、众数如下表所示:学校
平均数
中位数
众数
甲
67
60
60
乙
70
75
其中
(2)、(得出结论)①小明同学说:“这次竞赛我得了70分,在我们学校排名属中游略偏上!”由表中数据可知小明是校的学生;(填“甲”或“乙”)
②张老师从乙校随机抽取一名学生的竞赛成绩,试估计这名学生的竞赛成绩为优秀的概率为;
(3)、根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由.(至少从两个不同的角度说明推断的合理性)20. 阅读下面的解答过程,然后作答:有这样一类题目:将 化简,若你能找到两个数 m和n,使m2+n2=a 且 mn= ,则a+2 可变为m2+n2+2mn,即变成(m+n)2 , 从而使得 化简.
例如:∵5+2 =3+2+2 =( )2+( )2+2 =( + )2
∴ = = +
请你仿照上例将下列各式化简
(1)、(2)、 .21. 疫情期间,某学校准备购进一批红外线测温仪和口罩若干包.已知购买1个红外线测温仪和2包口罩共需460元;购买2个红外线测温仪和3包口罩共需880元.(1)、求一个红外线测温仪和一包口罩的售价各是多少元?(2)、学校准备购进红外线测温仪20个,口罩若干包(超过30包).某药店对这两种商品给出优惠活动,活动一:购买1个红外线测温仪送1包口罩;活动二:购买口罩30包以上,超出的部分按售价的五折优惠,红外线测温仪不打折.①设购买口罩 包,选择活动一的总费用为 元,选择活动二的总费用为 元,请分别求出 与 的函数关系式;
②学校计划购买80包口罩,选择活动一和活动二哪个更省钱?请说明理由
22. 如图①,在 中, 分别是 的高和角平分线,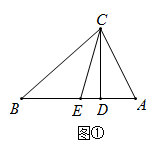 (1)、若 ,求 的度数(2)、若 ,则 (用含 的代数式表示);(3)、若将 换成钝角三角形,如图②,其他条件不变,试用含 的代数式表示 的度数,并说明理由;
(1)、若 ,求 的度数(2)、若 ,则 (用含 的代数式表示);(3)、若将 换成钝角三角形,如图②,其他条件不变,试用含 的代数式表示 的度数,并说明理由; (4)、如图③,若 是 外角 的平分线,交 延长线与点 ,且 ,则 (直接写出结果)
(4)、如图③,若 是 外角 的平分线,交 延长线与点 ,且 ,则 (直接写出结果) 23. 四边形 是一张放在平面直角坐标系中的长方形纸片, 为原点,点 在 轴上,点 在 轴上,
23. 四边形 是一张放在平面直角坐标系中的长方形纸片, 为原点,点 在 轴上,点 在 轴上, (1)、如图,在 上取一点 ,使得 沿 翻折后,点 落在 轴上,记作 点,求 点的坐标.(2)、求折痕 所在直线的解析式.(3)、在折痕 上是否存在一点 ,使 最小?若存在,直接写出 的最小值,若不存在,请说明理由.
(1)、如图,在 上取一点 ,使得 沿 翻折后,点 落在 轴上,记作 点,求 点的坐标.(2)、求折痕 所在直线的解析式.(3)、在折痕 上是否存在一点 ,使 最小?若存在,直接写出 的最小值,若不存在,请说明理由.