山西省朔州市怀仁市2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-03-08 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、a²+2a²=3a⁴ B、(-2x²)³=-8x⁶ C、(m－n)²=m²-n² D、b¹⁰÷b²=b⁵

查看试题解析
2. 将0.000073用科学记数法表示为（）

A、73×10^－⁶ B、0.73×10^－⁴ C、7.3×10^－⁴ D、7.3×10^－⁵

查看试题解析
3. 若实数a，b满足a²－4a＋4+(b－4)²=0，且a，b恰好是等腰△ABC两条边的长，则△ABC周长为（）

A、8 B、8或10 C、12 D、10

查看试题解析
4. 化简 $\frac{x}{x^{2} + 2 x + 1}$ ÷(1－ $\frac{1}{x + 1}$ )的结果是（）

A、 $\frac{1}{x + 1}$ B、 $\frac{1}{x - 1}$ C、x+1 D、x-1

查看试题解析
5. 某市铺设一条长660米的管道，为了尽量减少施工对城市交通造成的影响，实际施工时每天铺设的管道长比计划增加10%，结果提前6天完工，求实际每天铺设管道长度及实际施工天数，小明列出方程： $\frac{660}{x} - \frac{660}{x (1 + 10 %)}$ =6，题中x表示的量为（）

A、实际每天铺设管道长度 B、实际施工天数 C、计划施工天数 D、计划每天铺设管道的长度

查看试题解析
6. 已知一个等腰三角形两个内角度数之比为1：4，则这个等腰三角形顶角度数为（）

A、75° B、90° C、105° D、120°或20°

查看试题解析
7. 下列因式分解正确的是（）

A、m²+n²=(m+n)(m-n) B、a³-a=a(a+1)(a-1) C、a²-2a+1=a(a-2)+1 D、x²+2x-1=(x-1)²

查看试题解析
8. 下列图形：

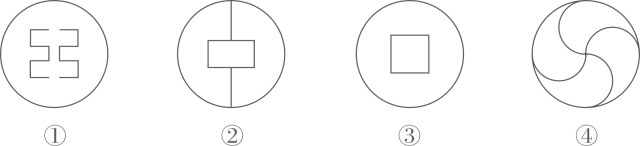
其中是轴对称图形且有两条对称轴的是（）

A、①② B、②③ C、②④ D、③④

查看试题解析
9. 4张长为a、宽为 $b (a > b)$ 的长方形纸片，按如图的方式拼成一个边长为 $(a + b)$ 的正方形，图中空白部分的面积为 $S_{1}$ ，阴影部分的面积为 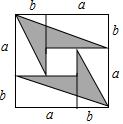$S_{2}$ ．若 $S_{1} = 2 S_{2}$ ，则a、b满足（）

A、 $2 a = 5 b$ B、 $2 a = 3 b$ C、 $a = 3 b$ D、 $a = 2 b$

查看试题解析
10. 如图，在△ABC中，AB=BC，∠ABC=90°，BM是AC边的中线，点D，E分别在边AC和BC上，DB=DE，EF⊥AC于点F，则以下结论；①∠DBM=∠CDE；②BN=DN；③AC=2DF；④S $_{Δ B D E}$ ﹤S $_{四边形 B M F E}$ 其中正确的结论是（）

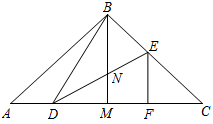A、①②③ B、②③④ C、①②④ D、①③

查看试题解析

二、填空题

11. 如果 $x^{2} - 10 x + m$ 是一个完全平方式，那么m的值是．

查看试题解析
12. 计算 $\frac{16 - a^{2}}{a^{2} + 8 a + 16}$ ÷ $\frac{a - 4}{2 a + 8}$ = ．

查看试题解析
13. 若3^m=4，3ⁿ=2，则9^2m-n=.

查看试题解析
14. 若x²+4x-4=0，则3（x-2）²-6(x+1)(x-1)的值为．

查看试题解析
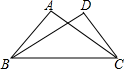15. 如图，已知 $∠ A B C = ∠ D C B$ ，添加下列条件中的一个：① $∠ A = ∠ D$ ，② $A C = D B$ ，③ $A B = D C$ ，其中不能确定 $Δ A B C$ ≌△ $Δ D C B$ 的是（只填序号）.

查看试题解析
16. 如图，∠C=90°，CB=CO，且点B坐标为（-2，0），则点C坐标为．

查看试题解析

三、解答题

17.

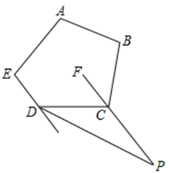
(1)、计算：（－ $\frac{1}{4}$ ）^-2-（ $\sqrt{2}$ ）⁰+（－5）⁹×（－0.2⁸）；

(2)、因式分解：（1-a）²+4（a-1）；

(3)、计算：（x+3）²－(x+2)(x-1)．

查看试题解析
18.

(1)、先化简，再求值： $\frac{1}{x - y} \cdot (\frac{2 y}{x + y} - 1)$ ÷ $\frac{1}{y^{2} - x^{2}}$ ，其中x=y+2020．

(2)、解方程： $\frac{3}{x^{2} - 9}$ - $\frac{1}{2 x - 6} = \frac{1}{2 x + 6}$ ．

查看试题解析
19. 如图，在五边形ABCDE中，∠A+∠B+∠E=310°，CF平分∠DCB，FC的延长线与五边形ABCDE外角平分线相交于点P，求∠P的度数

查看试题解析
20. 观察下列等式：
第1个等式： $\frac{2}{1} = \frac{1}{1} + \frac{1}{1}$

第2个等式： $\frac{2}{3} = \frac{1}{2} + \frac{1}{6}$

第3个等式： $\frac{2}{5} = \frac{1}{3} + \frac{1}{15}$

第4个等式： $\frac{2}{7} = \frac{1}{4} + \frac{1}{28}$

按照以上规律，解出下列问题：

(1)、第6个等式为：．

(2)、写出第n个等式：（用含n的等式表示）并证明．

查看试题解析
21. 抗洪抢险，需要在一定时间内筑起拦洪大坝，甲队单独做正好按期完成，而乙队由于人少，单独做则延期3小时才能完成．现甲、乙两队合作2小时后，甲队又有新任务，余下的由乙队单独做，刚好按期完成．求甲、乙两队单独完成全部工程各需要多少小时．

查看试题解析
22. 已知：AB⊥CD于点O，AB=AC=CD，点I是∠BAC，∠ACD的平分线的交点，连接IB，ID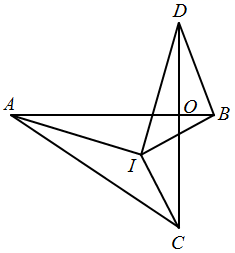

(1)、求证： $I A = I D$ 且 $I A ⊥ I D$ ；

(2)、填空：
①∠AIC+∠BID=度；

②S $_{Δ I B D}$ S $_{Δ A I C}$ (填“﹥”“﹤”“=”)

(3)、将（2）小题中的第②结论加以证明．

查看试题解析
23. 如图：已知点A（0，1），点B在第一象限，△OAB是等边三角形，点C是X轴上的动点，以AC为边作等边三角形△ACD(A、C、D三点按逆时针排列)，直线BD交Y轴于点E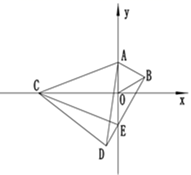

(1)、求证：△CAO≌△DAB；

(2)、点C运动时，点E是动点还是定点？若是动点，指出其运动路径；若是定点，求其坐标；

(3)、连接CE，若∠ACD=25°，求∠CED的度数．

查看试题解析