内蒙古自治区赤峰市宁城县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-03-08 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形：

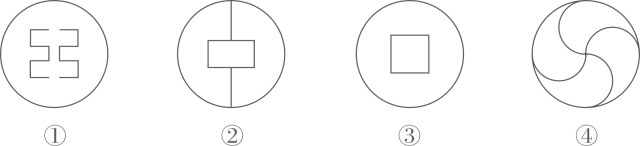
其中是轴对称图形且有两条对称轴的是（）

A、①② B、②③ C、②④ D、③④

查看试题解析
2. 如果分式 $\frac{6}{x - 2}$ 有意义，那么 $x$ 满足（）

A、 $x = 2$ B、 $x \neq 2$ C、 $x = 0$ D、 $x \neq 0$

查看试题解析
3. 下列各式不能用平方差公式计算的是（）

A、（2a－3b）（3a＋2b） B、（4a² －3bc）（ 4a² ＋3bc） C、（3a＋2b）（2b－3a） D、（3m＋5）（5－3m）

查看试题解析
4. 从正多边形的一个顶点可以引出5条对角线,则这个正多边形每个外角的度数为（）

A、135° B、45° C、60° D、120°

查看试题解析
5. 如图，在△ABC中，F是高AD和BE的交点，BC＝6，CD＝2，AD＝BD，则线段AF的长度为（）

A、2 B、1 C、4 D、3

查看试题解析
6.
如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点，若PA=2，则PQ的最小值为（）

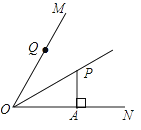A、1 B、2 C、3 D、4

查看试题解析

二、填空题

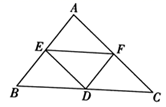
7. H7N9禽流感病毒的直径大约是0.00000008m，用科学记数法表示为m

查看试题解析
8. 分解因式a² b - ab² =

查看试题解析
9. 如图，在△ABC中，点E、F分别是AB、AC边上的点，EF∥BC，点D在BC边上，连接DE、DF请你添加一个条件，使△BED≌△FDE

查看试题解析
10. 若代数式 ${(m + 2)}^{0} + {(m - 2)}^{- 2}$ 有意义，则m的取值范围是.

查看试题解析
11. 若 $2^{x} = 3$ ， $2^{y} = 5$ ，则 $2^{x + y} =$ ．

查看试题解析
12. 如图，在Rt△ABC中，∠C=90°，∠B=30°，边AB的垂直平分线DE交AB于点E，交BC于点D，CD=3，则BC的长为。

查看试题解析
13. 等腰三角形一腰上的高与另一腰的夹角的度数为20°，则顶角的度数是．

查看试题解析
14. 如图，在△ABC中，将∠B、∠C按如图所示的方式折叠，点B、C均落于边BC上的点Q处，MN、EF为折痕，若∠A=82°，则∠MQE=

查看试题解析
15. 因式分解： $12 x^{2} - 3 y^{2} =$ .

查看试题解析

三、解答题

16. 解方程： $\frac{1}{x}$ - $\frac{5}{x + 3}$ =0

查看试题解析
17. 先化简，再求值： ${(2 x + 3 y)}^{2} - (2 x + y) (2 x - y)$ ，其中 $x = \frac{1}{3}$ ， $y = - \frac{1}{2}$ ．

查看试题解析
18. 如图，在平面直角坐标系中

(1)、请在图中作出△ABC关于直线m的轴对称图形△A $_{1}$ B $_{1}$ C $_{1}$

(2)、坐标系中有一点M(-3，3)，点M关于直线m的对称点为点N ，点N关于直线n的对称点为点E ，写出点N的坐标；点E的坐标．

查看试题解析
19. 已知：如图，点E、A、C在同一直线上，AB∥CD，AB＝CE，AC＝CD
求证：∠B＝∠E

查看试题解析
20. 如图，BD是△ABC的角平分线，AE丄BD交BD的'延长线于点E， ∠ABC = 72°，∠C：∠ADB =2：3，求∠BAC 和∠DAE 的度数.

查看试题解析
21. 如图①是一个长为2m、宽为2n的长方形，用剪刀沿图中的虚线（对称轴）剪开，把它分成四个形状和大小都相同的小长方形，然后按图②拼成一个正方形（中间是空的）

(1)、图②中画有阴影的小正方形的边长为（用含m、n的式子表示）

(2)、观察图②写出代数式（m+n） $^{2}$ 、（m-n） $^{2}$ 与mn之间的等量关系

(3)、根据（2）中的等量关系解决下面问题：若a+b=7，ab=5，求（a-b） $^{2}$ 的值

查看试题解析
22. 如图，在△ABC中，已知AB=AC，AB的垂直平分线交AB于点N，交AC于点M，连接MB

(1)、若∠ABC=65°，则∠NMA的度数为

(2)、若AB=10cm，△MBC的周长是18cm
①求BC的长度

②若点P为直线MN上一点，则△PBC周长的最小值为cm

查看试题解析
23. 问题：分解因式（a+b）² -2（a+b）+1
答：将“a+b”看成整体，设M=a+b，原式=M² -2M+1=（M-1）² ，将M还原，得原式=（a+b-1）²

上述解题用到的是“整体思想”，这是数学解题中常用的一种思想方法．

请你仿照上面的方法解答下列问题：

(1)、因式分解：（2a+b）² -9a² =

(2)、求证：（n+1）（n+2）（n² +3n）+1的值一定是某一个正整数的平方（n为正整数）

查看试题解析
24. 如图，△ABC是等边三角形，D是边AC的中点，EC⊥BC与点C，连接BD、DE、AE且CE=BD，
求证：△ADE为等边三角形

查看试题解析
25. 仙桃是遂宁市某地的特色时令水果．仙桃一上市，水果店的老板用2400元购进一批仙桃，很快售完；老板又用3700元购进第二批仙桃，所购件数是第一批的 $\frac{3}{2}$ 倍，但进价比第一批每件多了5元．

(1)、第一批仙桃每件进价是多少元？

(2)、老板以每件225元的价格销售第二批仙桃，售出80%后，为了尽快售完，剩下的决定打折促销．要使得第二批仙桃的销售利润不少于440元，剩余的仙桃每件售价至少打几折？（利润＝售价﹣进价）

查看试题解析
26. 如图①，∠BAD=90°，AB=AD，过点B作BC⊥AC于点C，过点D作DE⊥CA的延长线点E，由∠1+∠2=∠D+∠2=90°，得∠1=∠D，又∠ACB=∠AED=90°，AB=AD，得△ABC≌△DAE进而得到AC=DE，BC=AE，我们把这个数学模型称为“K字”模型或“一线三等角”模型．
请应用上述“一线三等角”模型，解决下列问题：

(1)、如图②，∠BAD=∠CAE=90°，AB=AD，AC=AE，连接BC、DE，且BC⊥AH于点H，DE与直线AH交于点G，求证：点G是DE的中点．

(2)、如图③，在平面直角坐标系中，点A为平面内任意一点，点B的坐标为（4，1），若△AOB是以OB为斜边的等腰直角三角形，请直接写出点A的坐标．

查看试题解析