河北省唐山市路北区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-03-08 类型：期末考试

进入出卷网下载

一、单选题

1. 要使分式 $\frac{x + 1}{x - 1}$ 有意义，则 $x$ 的取值应满足（）

A、 $x = - 1$ B、 $x = 1$ C、 $x \neq 1$ D、 $x \neq - 1$

查看试题解析
2. 下列各式中，从左到右的变形是因式分解的是（）

A、 $(a + 2) (a - 2) = a^{2} - 4$ B、 $a b + a c + d = a (b + c) + d$ C、 $x^{2} - 9 = {(x - 3)}^{2}$ D、 $a^{2} b - a b^{2} = a b (a - b)$

查看试题解析
3. 下列运算中，正确的是（）

A、 $- (m + n) = n - m$ B、 ${(m^{3} n^{2})}^{3} = m^{6} n^{5}$ C、 $m^{3} \cdot m^{2} = m^{5}$ D、 $n^{3} \div n^{3} = n$

查看试题解析
4. 下列数据能够组成三角形的是（）

A、1，2，3 B、3，4，5 C、4，4，8 D、4，5，10

查看试题解析
5. 下列手机屏幕解锁图形案是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 计算 $(\frac{x}{x - 2} - \frac{x}{x + 2}) \div \frac{4 x}{2 - x}$ 的结果是（）

A、- $\frac{1}{x + 2}$ B、 $\frac{1}{x + 2}$ C、-1 D、1

查看试题解析
7. 下列分式变形中，正确的是（）

A、 $\frac{a^{2} + b^{2}}{a + b} = a + b$ B、 $\frac{- x + y}{x + y} = - 1$ C、 $\frac{a}{b} = \frac{a m}{b m}$ D、 $\frac{{(n - m)}^{3}}{{(m - n)}^{2}} = n - m$

查看试题解析
8. 已知x＝3是分式方程 $\frac{k x}{x - 1} - \frac{2 k - 1}{x} = 2$ 的解，那么实数k的值为（）

A、－1 B、0 C、1 D、2

查看试题解析
9. 如图 $∠ 1 ， ∠ 2 ， ∠ 3$ 是正五边形 $A B C D E$ 的三个外角，若 $∠ A + ∠ B = 230 ° ，$ 则 $∠ 1 + ∠ 2 + ∠ 3$ =（）

A、 $140 °$ B、 $180 °$ C、 $230 °$ D、 $320 °$

查看试题解析
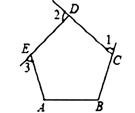10. 如图所示，在等边三角形ABC中，AD⊥BC，E为AD上一点，∠CED＝50°，则∠ABE等于（）

A、10° B、15° C、20° D、25°

查看试题解析
11. 如图，△ABC中，∠A=90°，AB=AC，BD平分∠ABE，DE⊥BC，如果BC=10 cm，则△DEC的周长是（）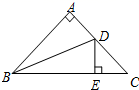

A、8 cm B、10 cm C、11 cm D、12 cm

查看试题解析
12. 三个连续奇数，若中间的一个为 $n$ ，则这三个连续奇数之积为（）

A、 $4 n^{3} - n$ B、 $n^{3} - 4 n$ C、 $8 n^{3} - 8 n$ D、 $n^{3} - n$

查看试题解析
13. 一个多边形截去一个角后，形成的另一个多边形的内角和是 $1620 °$ ，则原来多边形的边数是（）

A、11 B、12 C、11或12 D、10或11或12

查看试题解析
14. 如图，在锐角三角形 $A B C$ 中， $A B = 4$ ， $△ A B C$ 的面积为 $10$ ， $B D$ 平分 $∠ A B C$ ，若 $M$ 、 $N$ 分别是 $B D$ 、 $B C$ 上的动点，则 $C M + M N$ 的最小值为（）

A、4 B、5 C、4.5 D、6

查看试题解析

二、填空题

15. 分解因式： $m^{2} + 3 m =$ ．

查看试题解析
16. 若凸n边形的内角和为1260°，则从一个顶点出发引的对角线条数是

查看试题解析
17. 若 $x^{a} = 4$ ， $x^{b} = 3$ ， $x^{c} = 8$ ，则 $x^{2 a + b - c}$ 的值为．

查看试题解析
18. A、B两地相距36千米，一艘轮船从 $A$ 地顺流行至B地，又立即从B地逆流返回A地，共用9小时，已知水流速度为 $4$ 千米/时，若设该轮船在静水中的速度为 $x$ 千米时，则可列方程为．

查看试题解析

三、解答题

19. 计算： ${(x - 3)}^{2} - (4 x^{3} - 12 x^{2}) \div 2 x$

查看试题解析
20. 解方程：

(1)、 $\frac{3}{x} = \frac{1}{x - 2}$

(2)、 $\frac{3}{2 x - 2} - \frac{1}{x - 1} = 1$

查看试题解析
21. 如图①是一个长为2m、宽为2n的长方形，用剪刀沿图中的虚线（对称轴）剪开，把它分成四个形状和大小都相同的小长方形，然后按图②拼成一个正方形（中间是空的）

(1)、图②中画有阴影的小正方形的边长为（用含m、n的式子表示）

(2)、观察图②写出代数式（m+n） $^{2}$ 、（m-n） $^{2}$ 与mn之间的等量关系

(3)、根据（2）中的等量关系解决下面问题：若a+b=7，ab=5，求（a-b） $^{2}$ 的值

查看试题解析
22. 如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．
求证：

(1)、BC=AD；

(2)、△OAB是等腰三角形．

查看试题解析
23. 先化简，再求值： $(\frac{a^{2} + 1}{a - 2} - a) + \frac{4 a^{2} + 1}{2 - a}$ ，其中a是满足不等式组 ${\begin{array}{l} a - 2 \leq 0 \\ a > 0 \end{array}$ 的整数解．

查看试题解析
24. 如图，在 $△ A B C$ 中， $A B = A C$ ， $M$ ， $N$ 分别是 $A B$ ， $A C$ 边上的点，并且 $M N // B C$ ．

(1)、 $△ A M N$ 是否是等腰三角形？说明理由；

(2)、点 $P$ 是 $M N$ 上的一点，并且 $B P$ 平分 $∠ A B C$ ， $C P$ 平分 $∠ A C B$ ．
①求证： $△ B P M$ 是等腰三角形；

②若 $△ A B C$ 的周长为 $a$ ， $B C = b (a > 2 b)$ ，直接写出 $△ A M N$ 的周长（用含 $a$ ， $b$ 的式子表示）．

查看试题解析
25. 为响应稳书记“足球进校园”的号召，某学校在某商场购买甲、乙两种不同足球，购实甲种足球共花费2000元，购买乙种足球共花费1400元，购买甲种是球数量是购类乙种足球数量的2倍，且购买一个乙种足球比购买一个甲种足球多花20元.

(1)、求这间商场出售每个甲种足球、每个乙种足球的售价各是多少元；

(2)、按照实际需要每个班须配备甲足球2个，乙种足球1个，购买的足球能够配备多少个班级?

(3)、若另一学校用3100元在这商场以同样的售价购买这两种足球，且甲种足球与乙种足球的个数比为2：3，求这学校购买这两种足球各多少个?

查看试题解析
26. 如图，已知 $△ A B C$ 中， $A B = A C = 10$ 厘米， $B C = 8$ 厘米，点 $D$ 为 $A B$ 的中点．

(1)、如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
①若点Q的运动速度与点P的运动速度相等，经过1秒后， $△ B P D$ 与 $△ C Q P$ 是否全等，请说明理由；

②若点Q的运动速度与点P的运动速度不相等， $△ B P D$ 与 $△ C Q P$ 是否可能全等？若能，求出全等时点Q的运动速度和时间；若不能，请说明理由．

(2)、若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿 $△ A B C$ 三边运动，求经过多长时间点P与点Q第一次在 $△ A B C$ 的哪条边上相遇？

查看试题解析