初中数学湘教版九年级下册第一章 二次函数 单元测试（基础练）

试卷更新日期：2021-03-07 类型：单元试卷

进入 出卷网 下载

一、单选题

  • 1. 下列函数关系式中，一定是二次函数的是（  ）
    A、y=−x+3 B、y=ax2+2x−1 C、y=12x D、y=x2+x−2

    查看试题解析

  • 2. 若y=（a+2）x2-3x+2是二次函数，则a的取值范围是（   ）
    A、a≠0 B、a＞0 C、a＞2 D、a≠-2

    查看试题解析

  • 3. 已知二次函数 y=ax2+bx+c(a≠0) 图象上部分点的坐标 (x,y) 的对应值如表所示：

    x

    …

    0

    5

    4

    …

    y

    …

    0.37

    -1

    0.37

    …

    则方程 ax2+bx+1.37=0 的根是（   ）.

    A、0或4 B、5 或 4−5 C、4+5 或 5 D、无实根

    查看试题解析

  • 4. 抛物线y＝－3x2+2x－1的图象与坐标轴的交点个数是 （ ）
    A、无交点 B、1个 C、2个 D、3个

    查看试题解析

  • 5. 若抛物线 y=x2+ax+b 与x轴两个交点间的距离为4，称此抛物线为定弦抛物线.已知某定弦抛物线的对称轴为直线 x=2 ，将此抛物线向左平移2个单位，再向上平移3个单位，得到的新抛物线经过点（   ）
    A、(1,−6) B、(1,−1) C、(1,0) D、(1,8)

    查看试题解析

  • 6. 二次函数y = ax2-2x-3（a<0）的图象一定不经过的象限是（            ）
    A、第一象限 B、第二象限 C、第三象限 D、第四象限

    查看试题解析

  • 7. 已知二次函数的图象（0≤x≤4）如图，关于该函数在所给自变量的取值范围内，下列说法正确的是（　　）

    A、有最大值 1.5，有最小值﹣2.5 B、有最大值 2，有最小值 1.5 C、有最大值 2，有最小值﹣2 5 D、有最大值 2，无最小值

    查看试题解析

  • 8. 已知二次函数y＝ax2+bx+c（a≠0）图象如图所示，下列结论：

    ①abc＜0；②2a﹣b＜0；③4a﹣2b+c＞0；④点（﹣3，y1），（1，y2）都在抛物线上，则有y1＞y2.其中正确的结论有（   ）

    A、4个 B、3个 C、2个 D、1个

    查看试题解析

  • 9. 直线y＝bx+c与抛物线y＝ax2+bx+c（a＞0）在同一坐标系中大致图象可能是（   ）
    A、 B、     C、 D、

    查看试题解析

  • 10. 已知二次函数的图象经过P（2，2），顶点为O（0，0），将该图象向右平移，当它再次经过点P时，所得抛物线的函数表达式为（   ）
    A、y＝ 12 x2 B、y＝ 12 （x﹣2）2 C、y＝ 12 （x﹣4）2 D、y＝ 12 （x﹣2）2+2

    查看试题解析

  • 11. 关于二次函数 y=x2+2x−8 ，下列说法正确的是（    ）
    A、图象的对称轴在 y 轴的右侧 B、图象与 y 轴的交点坐标为 (0,8) C、图象与 x 轴的交点坐标为 (−2,0) 和 (4,0) D、y 的最小值为－9

    查看试题解析

  • 12. 某公园有一个圆形喷水池，喷出的水流呈抛物线状，一条水流的高度 h(m) 与水流时间 t(s) 之间的解析式为 h=30t−5t2 ，那么水流从抛出至落到地面所需要的时间是（   ）
    A、8s B、6s C、4s D、2s

    查看试题解析

二、填空题

  • 13. 若 y=(m+1)xm2−2m−1 是二次函数，则m= ， 其中自变量x的取值范围是 ．

    查看试题解析

  • 14. 已知二次函数 y=−2(x−1)2+k 的图象上有 A(−7,y1) ， B(2,y2) ， C(3,y3) 三个点.用“＜”连接 y1 ， y2 ， y3 的结果是.

    查看试题解析

  • 15. 如图，把抛物线y=-x2+2向右平移1个单位长度，则曲线AB扫过的面积（图中阴影部分）是.

    查看试题解析

  • 16. 写出一个二次函数，其图像满足：①开口向下；②与 y 轴交于点 (0 ， −3) ，这个二次函数的解析式可以是 ．

    查看试题解析

  • 17. 已知抛物线y = ax2+bx-2 （a≠0）的顶点在第三象限，且过点（1， 0），若a-b的值为整数，则b的值为 .

    查看试题解析

  • 18. 如图，小滕用铁栅栏及一面墙（墙足够长）围成了一个矩形自行车场地ABCD，在AB和BC边各有一个2m宽的小门（不用铁栅栏），小滕共用了铁栅栏40米，则矩形ABCD的面积的最大值为m2.

    查看试题解析

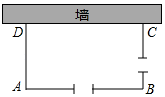
三、解答题

  • 19. 抛物线 y=ax2+bx+c(a≠0) 上部分点的横坐标x，纵坐标y的对应值如下表：

    x

    …

    -2

    -1

    0

    1

    2

    …

    y

    …

    0

    4

    6

    6

    4

    …

    求这个二次函数的表达式，并利用配方法求出此抛物线的对称轴、顶点坐标

    查看试题解析

  • 20. 已知二次函数 y = x 2 + x + a 的图象与x轴交于 A ( x 1 ， 0 ) 、 B ( x 2 ， 0 ) 两点，且 1 x 1 2 + 1 x 2 2 = 1 ，求a的值．

    查看试题解析

  • 21. 已知二次函数 y=−12x2−x+32 .

    (1)、在给定的直角坐标系中，画出这个函数的图象；
    (2)、根据图象，写出当y＜0时，x的取值范围；
    (3)、若将此图象沿x轴向右平移3个单位，请写出平移后图象所对应的函数关系式.

    查看试题解析

  • 22. 已知二次函数 y=x2−4x+3
    (1)、将 y=x2−4x+3 化成 y=a(x−h)2+k 的形式
    (2)、求出该二次函数的对称轴和顶点坐标
    (3)、当自变量x由5增大到8时，函数值y是怎样变化的

    查看试题解析

  • 23. 甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在O点正上方1m的P处发出一球，羽毛球飞行的高度y（m）与水平距离x（m）之间满足函数表达式 y=a(x-4)2+h ，已知点O与球网的水平距离为5m，球网的高度为1.55m．

    (1)、当a=- 124 时，①求h的值；②通过计算判断此球能否过网．
    (2)、若甲发球过网后，羽毛球飞行到与点O的水平距离为7m ， 离地面的高度为 125 m的Q处时，乙扣球成功，求a的值．

    查看试题解析

  • 24. 在平面直角坐标系 xoy 中，抛物线 y=mx2−2mx+m−3 与x轴交于点A、B．
    (1)、①求m的取值范围；

    ②当抛物线经过原点时，求抛物线的解析式；

    ③求抛物线的顶点坐标；

    (2)、若线段 AB 上有且只有5个点的横坐标为整数，求m的取值范围；
    (3)、若抛物线在 −3<x<0 这一段位于x轴下方，在 5<x<6 这一段位于x轴上方，求m的值．

    查看试题解析

  • 25. 某旅行社为吸引市民组团去某新开发的风景区旅游，推出了如下收费标准：如果旅游团人数不超过25人，人均旅游费用为1000元；如果旅游团人数超过25人，每增加1人，人均旅游费用降低20元，但人均旅游费用不得低于700元．设旅游团人数为 x 人．
    (1)、写出支付给旅行社费用 y （单位：元）关于 x 的函数关系式；
    (2)、某单位组织员工组团去此风景区旅游，共支付给旅行社旅游费用27000元，请问该单位这次共有多少人去旅游？

    查看试题解析

  • 26. 如图，有长为23m的篱笆，一面利用墙（墙的最大可用长度a为 10m ）围成中间隔有一道篱笆的矩形花圃，并且预留两个各0.5m的门，设花圃的宽AB为x m ，面积为 Sm2 ．

    (1)、求S与x的函数关系式，并写出自变量x的取值范围．
    (2)、如果要围成面积为 45m2 的花圃，AB的长是多少米？
    (3)、能围成面积为51m2的花圃吗？若能，请说明围法；若不能请说明理由．

    查看试题解析