初中数学湘教版九年级下册1.5二次函数的应用 同步练习
试卷更新日期:2021-03-07 类型:同步测试
一、单选题
-
1. 点C是线段AB上的一点,AB=1,分别以AC和CB为一边作正方形,用S表示这两个正方形的面积之和,下列判断正确的是( )
 A、当C是AB的中点时,S最小 B、当C是AB的中点时,S最大 C、当C为AB的三等分点时,S最小 D、当C是AB的三等分点时,S最大2. 一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
A、当C是AB的中点时,S最小 B、当C是AB的中点时,S最大 C、当C为AB的三等分点时,S最小 D、当C是AB的三等分点时,S最大2. 一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( ) A、此抛物线的解析式是y=- x2+3.5 B、篮圈中心的坐标是(4,3.05) C、此抛物线的顶点坐标是(3.5,0) D、篮球出手时离地面的高度是2m3. 如图是抛物线型拱桥,当拱顶离水面 时,水面宽 .若水面再下降 ,水面宽度为( ) .
A、此抛物线的解析式是y=- x2+3.5 B、篮圈中心的坐标是(4,3.05) C、此抛物线的顶点坐标是(3.5,0) D、篮球出手时离地面的高度是2m3. 如图是抛物线型拱桥,当拱顶离水面 时,水面宽 .若水面再下降 ,水面宽度为( ) . A、 B、 C、 D、4. 2019年女排世界杯于9月在日本举行,中国女排以十一连胜的骄人成绩卫冕冠军,充分展现了团队协作、顽强拼搏的女排精神.如图是某次比赛中垫球时的动作,若将垫球后排球的运动路线近似的看作拋物线,在同一竖直平面内建立如图所示的直角坐标系,已知运动员垫球时(图中点 )离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点 )越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点 )距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )
A、 B、 C、 D、4. 2019年女排世界杯于9月在日本举行,中国女排以十一连胜的骄人成绩卫冕冠军,充分展现了团队协作、顽强拼搏的女排精神.如图是某次比赛中垫球时的动作,若将垫球后排球的运动路线近似的看作拋物线,在同一竖直平面内建立如图所示的直角坐标系,已知运动员垫球时(图中点 )离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点 )越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点 )距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )
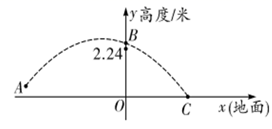 A、 B、 C、 D、5. 某幢建筑物,从10米高的窗口A用水管向外喷水,喷出的水流呈抛物线状(抛物线所在平面与墙面垂直,如图).如果抛物线的最高点M离墙1米,离地面 米,则水流落地点B离墙距离是( )
A、 B、 C、 D、5. 某幢建筑物,从10米高的窗口A用水管向外喷水,喷出的水流呈抛物线状(抛物线所在平面与墙面垂直,如图).如果抛物线的最高点M离墙1米,离地面 米,则水流落地点B离墙距离是( )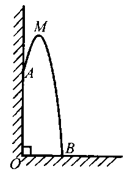 A、2米 B、3米 C、4米 D、5米6. 小敏用一根长为8cm的细铁丝围成矩形,则矩形的最大面积是( )A、4cm2 B、8cm2 C、16cm2 D、32cm27. 2019年10月31日,三大运营商宣布5G商用正式启动,5G时代大步流星地走来.某电器城准备销售一种型号的5G手机,在销售过程中发现,当零售价为每台4000元时,每天可以售出8台,日销售利润为4000元,当零售价每降低50元时,则每天多售出4台,下列结论正确的是( )A、 当零售价每降低200元时,日销售利润最大,最大利润为7200元 B、当零售价每降低100元和零售价每降低300元时,销售数量是一样的 C、手机的进价是每台500元 D、零售价越低,每天售出数量就越多,所以利润就越大8. 某旅游景点的收入受季节的影响较大,有时候出现赔本的经营状况.因此,公司规定:若无利润时,该景点关闭.经跟踪测算,该景点一年中的利润W(万元)与月份x之间满足二次函数W=﹣x2+16x﹣48,则该景点一年中处于关闭状态有( )月.A、5 B、6 C、7 D、89. 如图,点E,F,G,H分别是正方形ABCD边AB,BC,CD,DA上的点,且AE=BF=CG=DH.设A、E两点间的距离为x,四边形EFGH的面积为y,则y与x的函数图象可能为( )
A、2米 B、3米 C、4米 D、5米6. 小敏用一根长为8cm的细铁丝围成矩形,则矩形的最大面积是( )A、4cm2 B、8cm2 C、16cm2 D、32cm27. 2019年10月31日,三大运营商宣布5G商用正式启动,5G时代大步流星地走来.某电器城准备销售一种型号的5G手机,在销售过程中发现,当零售价为每台4000元时,每天可以售出8台,日销售利润为4000元,当零售价每降低50元时,则每天多售出4台,下列结论正确的是( )A、 当零售价每降低200元时,日销售利润最大,最大利润为7200元 B、当零售价每降低100元和零售价每降低300元时,销售数量是一样的 C、手机的进价是每台500元 D、零售价越低,每天售出数量就越多,所以利润就越大8. 某旅游景点的收入受季节的影响较大,有时候出现赔本的经营状况.因此,公司规定:若无利润时,该景点关闭.经跟踪测算,该景点一年中的利润W(万元)与月份x之间满足二次函数W=﹣x2+16x﹣48,则该景点一年中处于关闭状态有( )月.A、5 B、6 C、7 D、89. 如图,点E,F,G,H分别是正方形ABCD边AB,BC,CD,DA上的点,且AE=BF=CG=DH.设A、E两点间的距离为x,四边形EFGH的面积为y,则y与x的函数图象可能为( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在四边形 ABCD 中, AD∥BC , ∠A=45° , ∠C=90° , AD=4cm ,CD=3cm 、动点M,N同时从点A出发,点M以 cm/s 的速度沿 AB 向终点B运动,点N以2cm/s 的速度沿折线 AD-DC 向终点C运动.设点N的运动时间为ts ,△AMN 的面积为 Scm² ,则下列图象能大致反映S与t之间函数关系的是( )
10. 如图,在四边形 ABCD 中, AD∥BC , ∠A=45° , ∠C=90° , AD=4cm ,CD=3cm 、动点M,N同时从点A出发,点M以 cm/s 的速度沿 AB 向终点B运动,点N以2cm/s 的速度沿折线 AD-DC 向终点C运动.设点N的运动时间为ts ,△AMN 的面积为 Scm² ,则下列图象能大致反映S与t之间函数关系的是( )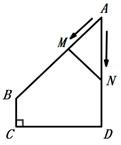 A、
A、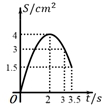 B、
B、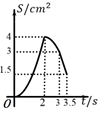 C、
C、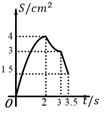 D、
D、
二、填空题
-
11. 如图,若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)之间具有的关系为h=20t﹣5t2 , 则小球从飞出到落地所用的时间为s.
 12. 将进货单价为70元的某种商品按零售单价100元售出时,每天能卖出40个,若这种商品的零售单价在一定范围内每降价1元,其日销量就增加2个,为了获取最大的日利润,则应把零售单价定为元.13. 为解决民生问题,国家对某药品价格分两次降价,该药品的原价是48元,降价后的价格是30元,若平均每次降价的百分率均为x,可列方程为 。14. 如图,在墙上绘制了几个相同的抛物线型图案.已知抛物线上B、C两点的高度相同,到墙边的OA的距离分别为0.5m,1.5m.若该墙的长度为12m,则最多可以连续绘制个这样的抛物线型图案.
12. 将进货单价为70元的某种商品按零售单价100元售出时,每天能卖出40个,若这种商品的零售单价在一定范围内每降价1元,其日销量就增加2个,为了获取最大的日利润,则应把零售单价定为元.13. 为解决民生问题,国家对某药品价格分两次降价,该药品的原价是48元,降价后的价格是30元,若平均每次降价的百分率均为x,可列方程为 。14. 如图,在墙上绘制了几个相同的抛物线型图案.已知抛物线上B、C两点的高度相同,到墙边的OA的距离分别为0.5m,1.5m.若该墙的长度为12m,则最多可以连续绘制个这样的抛物线型图案. 15. 某种正方形合金板材的成本y(元)与它的面积成正比,设边长为x厘米.当x=3时,y=18,那么当成本为72元时,边长为厘米.16. 定义:对角线互相垂直的四边形为垂美四边形.已知垂美四边形ABCD的对角线AC、BD满足AC+BD=12,则当AC=时,四边形ABCD的面积最大.
15. 某种正方形合金板材的成本y(元)与它的面积成正比,设边长为x厘米.当x=3时,y=18,那么当成本为72元时,边长为厘米.16. 定义:对角线互相垂直的四边形为垂美四边形.已知垂美四边形ABCD的对角线AC、BD满足AC+BD=12,则当AC=时,四边形ABCD的面积最大.三、解答题
-
17. 如图所示,公园要造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面距离最大,高度2.25m.若不计其他因素,那么水池的半径至少要多少米才能使喷出的水流不致落到池外?
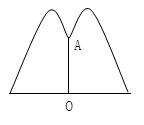 18. 某商场将进价40元一个的某种商品按50元一个售出时,每月能卖出500个,商场想了两个方案来增加利润:
18. 某商场将进价40元一个的某种商品按50元一个售出时,每月能卖出500个,商场想了两个方案来增加利润:方案一提高价格,但这种商品每个售价涨价1元,销售量就减少10个;
方案二:售价不变,但发资料做广告,已知这种商品每月的广告费用m(千元)与销售量倍数p关系为p=-0.4m2+2m,
试通过计算,请你判断商场为赚得更大的利润应选择哪种方案?请说明你判断的理由.
19. 如图,隧道的截面由抛物线和长方形构成.长方形的长为16m , 宽为6m , 抛物线的最高点C离路面AA1的距离为8m .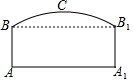 (1)、建立适当的坐标系,求出表示抛物线的函数表达式;(2)、一大型货车装载设备后高为7m , 宽为4m . 如果隧道内设双向行驶车道,那么这辆货车能否安全通过?20. 网络销售已经成为一种热门的销售方式为了减少农产品的库存,某市长亲自在某网络平台上进行直播销售板栗.为提高大家购买的积极性,直播时,板栗公司每天拿出2000元现金,作为红包发给购买者.已知该板栗的成本价格为6元/kg , 每日销售量y(kg)与销售单价x(元/kg)满足关系式:y=﹣100x+5000.经销售发现,销售单价不低于成本价格且不高于30元/kg . 当每日销售量不低于4000kg时,每千克成本将降低1元.设板栗公司销售该板栗的日获利为W(元).(1)、请求出日获利W与销售单价x之间的函数关系式;(2)、当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?21. 女生排球考试要求:垫球后,球在运动中离地面的最大高度至少为2米.某次模拟测试中,某女生在O处将球垫偏,之后又在A, B两处先后垫球,球沿抛物线C1 → C2 → C3运动(假设抛物线C1 , C2 , C3在同一平面内),最终正好在O处垫住,O处离地面的距离为1米.如图所示,以O为坐标原点1米为单位长度建立直角坐标系,x轴平行于地面水平直线m,已知点A( , ),点B的横坐标为 - ,抛物线C1和C3的表达式分别为 y = ax2- 2ax 和 y = 2ax2 + bx (a≠ 0).
(1)、建立适当的坐标系,求出表示抛物线的函数表达式;(2)、一大型货车装载设备后高为7m , 宽为4m . 如果隧道内设双向行驶车道,那么这辆货车能否安全通过?20. 网络销售已经成为一种热门的销售方式为了减少农产品的库存,某市长亲自在某网络平台上进行直播销售板栗.为提高大家购买的积极性,直播时,板栗公司每天拿出2000元现金,作为红包发给购买者.已知该板栗的成本价格为6元/kg , 每日销售量y(kg)与销售单价x(元/kg)满足关系式:y=﹣100x+5000.经销售发现,销售单价不低于成本价格且不高于30元/kg . 当每日销售量不低于4000kg时,每千克成本将降低1元.设板栗公司销售该板栗的日获利为W(元).(1)、请求出日获利W与销售单价x之间的函数关系式;(2)、当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?21. 女生排球考试要求:垫球后,球在运动中离地面的最大高度至少为2米.某次模拟测试中,某女生在O处将球垫偏,之后又在A, B两处先后垫球,球沿抛物线C1 → C2 → C3运动(假设抛物线C1 , C2 , C3在同一平面内),最终正好在O处垫住,O处离地面的距离为1米.如图所示,以O为坐标原点1米为单位长度建立直角坐标系,x轴平行于地面水平直线m,已知点A( , ),点B的横坐标为 - ,抛物线C1和C3的表达式分别为 y = ax2- 2ax 和 y = 2ax2 + bx (a≠ 0).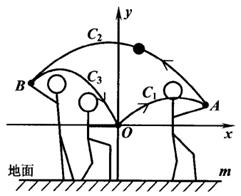 (1)、求抛物线C1的函数表达式.(2)、第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由.(3)、为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该女生第三次垫球处B 离地面的高度至少为多少米?
(1)、求抛物线C1的函数表达式.(2)、第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由.(3)、为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该女生第三次垫球处B 离地面的高度至少为多少米?