初中数学湘教版七年级下册第二章整式的乘法单元测试（提高篇）

试卷更新日期：2021-03-07 类型：单元试卷

进入出卷网下载

一、单选题

1. 若 $x^{2} - x - m = (x + n) (x + 7)$ ，则 $m - n$ 的值为（）

A、-64 B、-48 C、48 D、64

查看试题解析
2. 我们知道：若a^m＝aⁿ（a＞0且a≠1），则m＝n.设5^m＝3，5ⁿ＝15，5^p＝75.现给出m，n，p三者之间的三个关系式：①m+p＝2n；②m+n＝2p﹣1；③n²﹣mp＝1.其中正确的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
3. 已知多项式 $(x^{2} - m x + 1) (x - 2)$ 的积中x的一次项系数为零，则m的值是（）

A、1 B、–1 C、–2 D、 $- \frac{1}{2}$

查看试题解析
4. 如图所示，以长方形 $A B C D$ 的各边为直径向外作半圆，若四个半圆的周长之和为 $14 π$ ，面积之和为 $29 π$ ，则长方形 $A B C D$ 的面积为（）

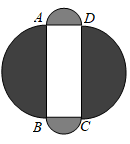A、10 B、20 C、40 D、80

查看试题解析
5. 已知 M = a² - a ， N = a -1（ a 为任意实数），则 M 、 N 的大小关系为（）

A、M＞ N B、M≥N C、M＜ N D、M≤ N

查看试题解析
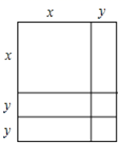6. 通过计算几何图形的面积可表示一些代数恒等式，小明从图中得到 $4$ 个代数恒等式：① $x (x + y) = x^{2} + x y$ ；② $x^{2} + 3 x y + 2 y^{2} = (x + y) (x + 2 y)$ ；③ ${(x + 2 y)}^{2} = x^{2} + 4 x y + 4 y^{2}$ ；④ $x^{2} + 2 x y + y^{2} = {(x + y)}^{2}$ 其中正确的有（）

A、②③ B、①②③ C、①②④ D、①②③④

查看试题解析
7. 已知实数 $a, b$ 满足 $a > b$ ，且 $a + b = 5, a b = - \frac{11}{4}$ ，则a-b的值为（）

A、6 B、-6 C、14 D、-14

查看试题解析
8. 如果四个互不相同的正整数m，n，p，q满足(6-m)(6-n)(6-p)(6-q)=4，那么m+n+p+q=(　　)

A、24　　　　 B、25　　　　　 C、26　　　 D、28

查看试题解析
9. 我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在 ${(a + b)}^{n} (n$ 为非负整数）的展开式中，把各项系数按一定的规律排成右表（展开后每一项按 $a$ 的次数由大到小的顺序排列）．人们把这个表叫做“杨辉三角”．据此规律，则 ${(x + 1)}^{2019}$ 展开式中含 $x^{2018}$ 项的系数是 $($ 　　 $)$

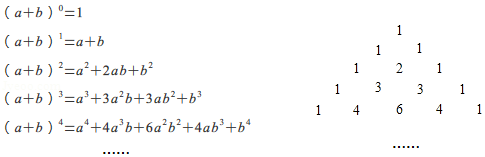A、2016 B、2017 C、2018 D、2019

查看试题解析
10. 如图，有两个正方形A ， B ，现将B放在A的内部得图甲，将A ， B并列放置后构造新的正方形得图乙。若图甲和图乙中阴影部分的面积分别为3和30，则正方形A、B的面积之和为（）

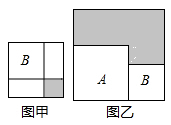A、33 B、30 C、27 D、24

查看试题解析
11. 观察下列各式及其展开式：（）
${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$

${(a + b)}^{4} = a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}$

${(a + b)}^{5} = a^{5} + 5 a^{4} b + 10 a^{3} b^{2} + 10 a^{2} b^{3} + 5 a b^{4} + b^{5}$

……

你猜想 ${(a + b)}^{10}$ 的展开式第三项的系数是（）

A、66 B、55 C、45 D、36

查看试题解析
12. 不论x、y为什么实数，代数式x²+y²+2x﹣4y+7的值（）

A、总不小于2 B、总不小于7 C、可为任何实数 D、可能为负数

查看试题解析

二、填空题

13. 观察下列各数，按照某种规律在横线上填上一个适当的数。
$- \frac{1}{4}$ ， $\frac{2}{8}$ ， $- \frac{3}{16}$ ， $\frac{4}{32}$ ， $- \frac{5}{64}$ ，.

查看试题解析
14. 观察、归纳：
（x﹣1）（x+1）＝x²﹣1；

（x﹣1）（x²+x+1）＝x³﹣1；

（x﹣1）（x³+x²+x+1）＝x⁴﹣1；

…

请你根据以上等式的规律，完成下列问题：

⑴（x﹣1）（xⁿ+…+x²+x+1）＝﹣1；

⑵计算：1+2+2²+…+2²⁰¹⁹＝．

查看试题解析
15. $(3 - 1) (3 + 1) (3^{2} + 1) (3^{4} + 1) ... (3^{32} + 1) + 1$ 的个位数字是．

查看试题解析
16. 一个自然数若能表示为两个自然数的平方差，则这个自然数称为“智慧数”．比如：2²-1²=3，则3就是智慧数；2²-0²=4，则4就是智慧数．
从0开始第7个智慧数是；不大于200的智慧数共有．

查看试题解析
17. 在2001、2002、…、2010这10个数中，不能表示成两个平方数差的数有个。

查看试题解析
18. 已知a²+ab+b²=7，a²-ab+b²=9，则（a+b）²= ．

查看试题解析

三、解答题

19. 用乘法公式计算下列各式的值

(1)、 $2000^{2} - 1999 \times 2001$

(2)、(2+1)(2²+1)(2⁴+1)⋯(2²ⁿ+1)

查看试题解析
20. 计算：（a－b）^2m-1·（b－a）^2m·（a－b）^2m+1 ，其中m为正整数．

查看试题解析
21. 证明：两个连续奇数的平方差是8的倍数，并且等于这两个数的和的两倍．

查看试题解析
22. 阅读探究，理解应用，根据乘方的意义填空，并思考：

(1)、 $2^{5} \times 2^{2} = (2 \times 2 \times 2 \times 2 \times 2) \times (2 \times 2) = 2^{()}$

(2)、 $a^{3} \cdot a^{2} = (a \cdot a \cdot a) \cdot (a \cdot a) = a^{()}$

(3)、 $5^{m} \times 5^{n} = (5 \times 5 \times \dots \times 5) \times (5 \times 5 \times \dots \times 5) = 5^{()}$ （m，n是正整数）
一般地，对于任意底数a与任意正整数m，n，则有： $a^{m} \cdot a^{n} =$

根据你发现的规律，完成下列问题：

计算： $b^{5} \cdot b =$ ； $y^{2 n} \cdot y^{n + 1} =$ ；

$(- \frac{1}{2}) \times {(- \frac{1}{2})}^{2} \times {(- \frac{1}{2})}^{3} =$ ；

(4)、已知 $a^{m} = 5$ ， $a^{n} = 125$ ，求 $a^{m + n}$ 的值．

查看试题解析
23. 已知 ${(a b)}^{2} = a^{2} b^{2}$ ， ${(a b)}^{3} = a^{3} b^{3}$ ， ${(a b)}^{4} = a^{4} b^{4}$ ．

(1)、当 $a = 1$ ， $b = - 2$ 时， ${(a b)}^{5} =$ ， $a^{5} b^{5} =$ ．

(2)、当 $a = - 1$ ， $b = 10$ 时， ${(a b)}^{6} =$ ， $a^{6} b^{6} =$ ．

(3)、观察（1）和（2）的结果，可以得出结论： ${(a b)}^{n} =$ （n为正整数）．

(4)、此性质可以用来进行积的乘方运算，反之仍然成立．如 $a^{2} b^{2} = {(a b)}^{2}$ ， $a^{3} b^{3} = {(a b)}^{3}$ ，…．应用上述等式，求 ${(- \frac{1}{4})}^{2019} \times 4^{2020}$ 的值．

查看试题解析
24. 好学小东同学，在学习多项式乘以多项式时发现：( $\frac{1}{2}$ x+4)(2x+5)(3x-6)的结果是一个多项式，并且最高次项为： $\frac{1}{2}$ x•2x•3x＝3x³ ，常数项为：4×5×(-6)=-120，那么一次项是多少呢？要解决这个问题，就是要确定该一次项的系数．根据尝试和总结他发现：一次项系数就是： $\frac{1}{2}$ ×5×(-6)+2×(-6)×4+3×4×5＝-3，即一次项为-3x ．
请你认真领会小东同学解决问题的思路，方法，仔细分析上面等式的结构特征．结合自己对多项式乘法法则的理解，解决以下问题．

(1)、计算(x+2)(3x+1)(5x-3)所得多项式的一次项系数为．

(2)、( $\frac{1}{2}$ x+6)(2x+3)(5x-4)所得多项式的二次项系数为．

(3)、若计算(x²+x+1)(x²-3x+a)(2x-1)所得多项式不含一次项，求a的值；

(4)、若(x+1)²⁰²¹=a₀x²⁰²¹+a₁x²⁰²⁰+a₂x²⁰¹⁹+···+a₂₀₂₀x+a₂₀₂₁ ，则a₂₀₂₀= ．

查看试题解析
25. 某同学利用若干张正方形纸片进行以下操作：

(1)、从边长为a的正方形纸片中减去一个边长为b的小正方形，如图1，再沿线段AB把纸片剪开，最后把剪成的两张纸片拼成如图2的等腰梯形，这一过程所揭示的公式是.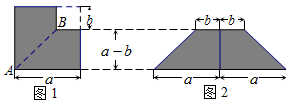

(2)、先剪出一个边长为a的正方形纸片和一个边长为b的正方形纸片，再剪出两张边长分别为a和b的长方形纸片，如图3，最后把剪成的四张纸片拼成如图4的正方形.这一过程你能发现什么代数公式？

(3)、先剪出两个边长为a的正方形纸片和一个边长为b的正方形纸片，再剪出三张边长分别为a和占的长方形纸片，如图5，你能否把图5中所有纸片拼成一个长方形？
如果可以，请画出草图，并写出相应的等式.如果不能，请说明理由.

查看试题解析
26. 阅读材料：如果一个数的平方等于﹣1，记为i²＝﹣1，这个数i叫做虚数单位，那么形如a+bi（a ， b为实数）的数就叫做复数，a叫这个复数的实部，b叫做这个复数的虚部．它有如下特点：
①它的加，减，乘法运算与整式的加，减，乘法运算类似例如计算：

（2+i）+（3﹣4i）＝（2+3）+（1﹣4）i＝5﹣3i；（3+i）i＝3i+i²＝3i﹣1

②若他们的实部和虚部分别相等，则称这两个复数相等若它们的实部相等，虚部互为相反数，则称这两个复数共轭，如1+2i的共轭复数为1﹣2i ．

(1)、填空：（3i﹣2）（3+i）＝；（1+2i）³（1﹣2i）³＝；

(2)、若a+bi是（1+2i）²的共轭复数，求（b﹣a）^a的值；

(3)、已知（a+i）（b+i）＝1﹣3i ，求（a²+b²）（i²+i³+i⁴+…+i²⁰¹⁹）的值．

查看试题解析

初中数学湘教版七年级下册第二章 整式的乘法 单元测试（提高篇）

一、单选题

二、填空题

三、解答题

初中数学湘教版七年级下册第二章整式的乘法单元测试（提高篇）