初中数学湘教版七年级下册2.2.1平方差公式同步训练

试卷更新日期：2021-03-07 类型：同步测试

进入出卷网下载

一、单选题

1. 计算 $(a + 2) (2 - a)$ 的结果是（）

A、2a-4 B、 $a^{2} - 4$ C、 $4 - a^{2}$ D、 $a^{2} - 2 a + 4$

查看试题解析
2. 下列多项式乘法中不能用平方差公式计算的是（）

A、(a³+b³)(a³﹣b³) B、(a²+b²)(b²﹣a²) C、(2x²y+1)(2x²y﹣1) D、(x²﹣2y)(2x+y²)

查看试题解析
3. 如图在边长为a的正方形中挖掉一个边长为b的小正方形(a＞b)．把余下的部分剪拼成一个长方形，通过计算阴影部分的面积，验证了一个等式，则这个等式是（）

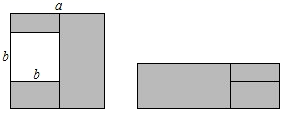A、a²﹣2ab+b²＝(a﹣b)² B、a²﹣ab＝a(a﹣b) C、a²﹣b²＝(a﹣b)² D、a²﹣b²＝(a+b)(a﹣b)

查看试题解析
4. 在下列多项式中，与 $- a + b$ 相乘的结果是 $a^{2} - b^{2}$ 的多项式是（）

A、 $a - b$ B、 $a + b$ C、 $- a + b$ D、 $- a - b$

查看试题解析
5. 下列各式中，能用平方差公式计算的是（）

A、 $(1 - 2 b) (2 b - 1)$ B、 $(- 1 - 2 b) (1 + 2 b)$ C、 $(- 1 - 2 b) (- 1 + 2 b)$ D、 $(1 - 2 b) (1 + 2 a)$

查看试题解析
6. 下列运用平方差公式计算，错误的是（）.

A、 $(a + b) (a - b) = a^{2} - b^{2}$ B、 $(x + 1) (x - 1) = x^{2} - 1$ C、 $(2 x + 1) (2 x - 1) = 2 x^{2} - 1$ D、 $(- a + b) (- a - b) = a^{2} - b^{2}$

查看试题解析
7. 为了应用平方差公式计算（a﹣b+c）（a+b﹣c），必须先适当变形，下列变形中，正确的是（）

A、[(a+c)﹣b] [(a﹣c)+b] B、[(a﹣b)+c][(a+b)﹣c] C、[a﹣(b+c)] [a+(b﹣c)] D、[a﹣(b﹣c)] [a+(b﹣c)]

查看试题解析
8. 已知 $a + b = 7$ ， $a - b = 8$ 则 $a^{2} - b^{2}$ 的值是（）

A、11 B、15 C、56 D、60

查看试题解析
9. 计算（x⁴+1）（x²+1）（x+1）（x﹣1）的结果是（）

A、x $^{8}$ +1 B、x $^{8}$ ﹣1 C、（x+1） $^{8}$ D、（x﹣1） $^{8}$

查看试题解析
10. 分别表示出下图阴影部分的面积，可以验证公式（）

A、(a+b)²=a²+2ab+b² B、(a-b)²=a²-2ab+b² C、a²-b²=(a+b)(a-b) D、(a+2b)(a-b)=a²+ab-2b²

查看试题解析

二、填空题

11. 若 $a + b = \frac{1}{3}, a - b = - 3$ ，则 $a^{2} - b^{2}$ =.

查看试题解析
12. 计算： $2021 \times 2019 - 2020^{2} =$

查看试题解析
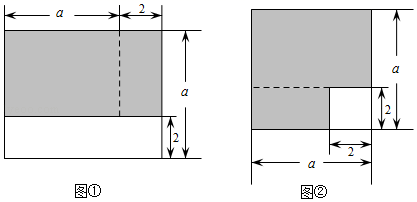
13. 如果有理数x，y满足方程组 ${\begin{array}{l} x + y = 4 \\ 2 x - 2 y = 1 \end{array}$ 那么x²－y²＝.

查看试题解析
14. 如图，利用图①和图②的阴影面积相等，写出一个正确的等式．

查看试题解析

三、综合题

15. 计算： $10 \frac{1}{7} \times 9 \frac{6}{7}$

查看试题解析
16. 计算： ${(\sqrt{3} - \sqrt{2})}^{2} \times {(\sqrt{3} + \sqrt{2})}^{2}$

查看试题解析
17. 对于算式 $2 (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) (3^{16} + 1) (3^{32} + 1) + 1$ .

(1)、不用计算器，你能计算出来吗；

(2)、求出它计算的结果的个位是几.

查看试题解析
18. 老师在黑板上写了三个算式，希望同学们认真观察，发现规律.请你结合这些算式，解答下列问题：
请观察以下算式：

① $3^{2} - 1^{2} = 8 \times 1$ ；

② $5^{2} - 3^{2} = 8 \times 2$ ；

③ $7^{2} - 5^{2} = 8 \times 3$ ；

……

试写出符合上述规律的第五个算式；

验证：设两个连续奇数为2n+1， $2 n - 1$ (其中 $n$ 为正整数)，并说明它们的平方差是8的倍数；

查看试题解析
19. 如图1，边长为 $a$ 的大正方形有一个边长为 $b$ 的小正方形，把图1中的阴影部分拼成一个长方形（如图2所示）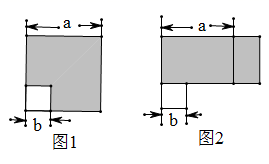

(1)、如图1，可以求出阴影部分的面积是（写成平方差的形式）

(2)、如图2，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是，长是，面积是.（写成多项式乘法形式）

(3)、比较左、右两图的阴影部分面积，可以得到公式.

(4)、请应用这个公式完成下列各题：
①已知 $4 m^{2} - n^{2} = 12$ ， $2 m + n = 4$ ，则 $2 m - n =$ .

②计算： $2020^{2} - 2018 \times 2022$

③计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \dots (1 - \frac{1}{2019^{2}}) (1 - \frac{1}{2020^{2}})$

查看试题解析

初中数学湘教版七年级下册2.2.1平方差公式 同步训练

一、单选题

二、填空题

三、综合题

初中数学湘教版七年级下册2.2.1平方差公式同步训练