初中数学湘教版七年级下册第一章二元一次方程组单元测试（提高练）

试卷更新日期：2021-03-07 类型：单元试卷

进入出卷网下载

一、单选题

1. 方程(m－2 016)x^|m|^－^{2 015}＋(n＋4)y^|n|^－³＝2 018是关于x、y的二元一次方程，则(　　)

A、m＝±2 016；n＝±4 B、m＝2 016，n＝4 C、m＝－2 016，n＝－4 D、m＝－2 016，n＝4

查看试题解析
2. 把一根长为13m的绳子截成1m和2m两种规格的小段，要求每种规格的绳子至少有一根，且无余料，则有（）种不同的截法

A、4种 B、5种 C、6种 D、7种

查看试题解析
3. 已知关于x，y的方程组 ${\begin{cases} 3 x - 5 y = 2 a \\ x - 2 y = a - 5 \end{cases}$ ，则下列结论中正确的是（）
①当a=5时，方程组的解是 ${\begin{cases} x = 10 \\ y = 20 \end{cases}$ ②当x，y的值互为相反数时，a=20；③不存在一个实数a使得x=y；④若2^2x-3y=2⁷ ，则a=2。

A、①②④ B、①②③ C、②③④ D、②③

查看试题解析
4. 如果方程组 ${\begin{cases} a x - b y =13 \\ 4x-5y=41 \end{cases}$ 与 ${\begin{cases} a x + b y =3 \\ 2x+3y=-7 \end{cases}$ 有相同的解，则a，b的值是（）

A、 ${\begin{cases} a = 2 \\ b = 1 \end{cases}$ B、 ${\begin{cases} a = 2 \\ b = - 3 \end{cases}$ C、 ${\begin{cases} a = \frac{5}{2} \\ b = 1 \end{cases}$ D、 ${\begin{cases} a = 4 \\ b = - 5 \end{cases}$

查看试题解析
5. 使方程组 ${\begin{cases} 2 x + m y = 16 \\ x - 2 y = 0 \end{cases}$ 有自然数解的整数m（）

A、只有5个 B、只能是偶数 C、是小于16的自然数 D、是小于32的自然数

查看试题解析
6. 如图，在数轴上标出若干个点，每相邻的两个点之间的距离都是1个单位，点A，B，C，D表示的数分别是整数a、b、c、d，且满足 $2 a - 3 d = - 19$ ，则 $b + c$ 的值为（　）

A、 $- 3$ B、 $- 2$ C、 $- 1$ D、 $0$

查看试题解析
7. 若关于x、y的方程组 ${\begin{array}{l} x + y = 3 k \\ x - y = 7 k \end{array}$ 的解满足方程2x＋3y＝6，那么k的值为（）

A、－ $\frac{3}{2}$ B、 $\frac{3}{2}$ C、－ $\frac{2}{3}$ D、 $\frac{2}{3}$

查看试题解析
8. 用加减法解方程组 ${\begin{matrix} 2 x + 3 y = 1 \\ 3 x - 2 y = 8 \end{matrix}$ 时，要使两个方程中同一未知数的系数相等或互为相反数，有以下四种变形：
$① {\begin{matrix} 6 x + 9 y = 1 \\ 6 x - 4 y = 8 \end{matrix} \begin{matrix} \end{matrix} ② {\begin{matrix} 4 x + 6 y = 1 \\ 9 x - 6 y = 8 \end{matrix} \begin{matrix} \end{matrix} ③ {\begin{matrix} 6 x + 9 y = 3 \\ - 6 x + 4 y = - 16 \end{matrix} \begin{matrix} \end{matrix} ④ {\begin{matrix} 4 x + 6 y = 2 \\ 9 x - 6 y = 24 \end{matrix}$

其中正确的是（）

A、②④ B、③④ C、①③ D、①②

查看试题解析
9. 欣欣幼儿园购买了90张等边三角形彩纸与50张正方形彩纸(如图1)，准备制作如图2所示的甲、乙两种图案，如果购买的彩纸刚好全部用完，则可以制作甲、乙两种图案共（）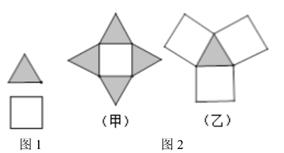

A、10个 B、20个 C、30个 D、40个

查看试题解析
10. 用白铁皮做罐头盒，每张铁皮可做盒身25个，或做盒底40个，一个盒身与两个盒底配成一套罐头盒．现有36张白铁皮，用多少张制盒身，多少张制盒底可以使盒身与盒底正好配套？
①设用x张制盒身，可得方程2×25x＝40(36﹣x)；

②设用x张制盒身，可得方程25x＝2×40(36﹣x)；

③设用x张制盒身，y张制盒底，可得方程组 ${\begin{matrix} \end{matrix} \begin{matrix} x + y = 36 \\ 2 \times 25 x = 40 y \end{matrix}$ ；

④设用x张制盒身，y张制盒底，可得方程组 ${\begin{matrix} \end{matrix} \begin{matrix} x + y = 36 \\ 25 x = 2 \times 40 y \end{matrix}$ ；其中正确的是（）

A、①④ B、②③ C、②④ D、①③

查看试题解析
11. 一块直角三角板按如图的方式摆放在讲台上，且∠1的度数比∠2的度数大56°，若设∠1=x°，∠2=y°，则可得到的方程组为（）

A、 ${\begin{cases} x = y - 56 \\ x + y = 180 \end{cases}$ B、 ${\begin{cases} x = y + 56 \\ x + y = 180 \end{cases}$ C、 ${\begin{cases} x = y - 56 \\ x + y = 90 \end{cases}$ D、 ${\begin{cases} x = y + 56 \\ x + y = 90 \end{cases}$

查看试题解析
12. 对于代数式ax²﹣2bx﹣c，当x取﹣1时，代数式的值为2，当x取0时，代数式的值为1，当x取3时，代数式的值为2，则当x取2时，代数式的值是（）

A、1 B、3 C、4 D、5

查看试题解析

二、填空题

13. 已知关于x，y的二元一次方程组 ${\begin{array}{l} a x + b y = 7 \\ b x + a y = 8 \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ ，那么关于m，n的二元一次方程组 ${\begin{array}{l} a (m + n) + b (m - n) = 7 \\ b (m + n) + a (m - n) = 8 \end{array}$ 的解为．

查看试题解析
14. 对于有理数，规定新运算：x※y=ax+by+xy，其中a、b是常数，等式右边的是通常的加法和乘法运算．已知：2※1=7，（﹣3）※3=3，则 $\frac{1}{3}$ ※b= ．

查看试题解析
15. 已知关于x,y的方程组2x+y=3m，x-4y=-2m的解也是方程y+2m=1+x的一组解,则m=

查看试题解析
16. 对有理数x ， y定义一种新运算“*”：x*y＝ax＋by ，其中a ， b为常数．等式右边是通常的加法和乘法运算．已知3*5＝15，4*7＝28，那么a＋b＝．

查看试题解析
17.
如图，两根铁棒直立于桶底水平的木桶中，在桶中加入水后，一根铁棒的 $\frac{1}{3}$ 露出水面，另一根铁棒的 $\frac{1}{4}$ 露出水面．两根铁棒长度之和为34cm，此时木桶中水的深度是　 cm．

查看试题解析
18. 我市某重点中学校团委、学生会发出倡议，在初中各年级捐款购买书籍送给我市贫困地区的学校．初一年级利用捐款买甲、乙两种自然科学书籍若干本，用去5324元；初二年级买了A、B两种文学书籍若干本，用去4840元，其中A、B的数量分别与甲、乙的数量相等，且甲种书与B种书的单价相同，乙种书与A种书的单价相同．若甲、乙两种书的单价之和为121元，则初一和初二两个年级共向贫困地区的学校捐献了本书．

查看试题解析

三、解答题

19.

(1)、解方程组： ${\begin{array}{l} x^{2} + y^{2} - 11 = 0 \\ \sqrt{2} x - 4 y + 10 = 0 \end{array}$

(2)、 ${\begin{array}{l} (x + 3) (y - 2) = (x - 3) (y + 10) \\ (x - 1) (y + 3) = (x + 2) (y + 12) \end{array}$

查看试题解析
20. 已知关于x、y的方程组
${\begin{matrix} 2 x + 3 y = 6 ① \\ a x + 6 y = 12 ② \end{matrix}$
问a为何值时，方程组有无数多组解?a为何值时，只有一组解?

查看试题解析
21. 已知二元一次方程 $a x + 3 y + b =0$ （ $a$ 、 $b$ 均为常数，且 $a \neq 0$ ）

(1)、当 $a = 2, b = - 4$ 时，用x的代数式表示y；

(2)、若 ${\begin{array}{l} x = a + 2 b \\ y = \frac{1}{3} (b^{2} - b) \end{array}$ 是该二元一次方程的一个解；
①探索 $a 与 b$ 关系，并说明理由；

②若该方程有一个解与 $a 、 b$ 的取值无关，请求出这个解.

查看试题解析
22. 某旅行社拟在暑假期间面向襄阳学生推出“汉城文化—日游”活动，收费标准如下：

人数 $m$

0＜ $m$ ≤100

100＜ $m$ ≤200

$m$ ＞200

收费标准(元／人)

90

85

75

甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人，乙校报名参加的学生人数少于100人.经核算，若两校分别组团共需花费20800元，若两校联合组团只需花费18000元.

(1)、两所学校报名参加旅游的学生人数之和超过200人吗?为什么?求出两校报名人数之和.

(2)、两所学校报名参加旅游的学生各有多少人.

查看试题解析
23. 为了防治“新型冠状病毒”，我市某小区准备用5400元购买医用口罩和洗
手液发放给本小区住户．若医用口罩买800个，洗手液买120瓶，则钱还缺200元；若医用口罩买1200个，洗手液买80瓶，则钱恰好用完．

(1)、求医用口罩和洗手液的单价；

(2)、由于实际需要，除购买医用口罩和洗手液外，还需增加购买单价为6元的N95口罩．若需购买医用口罩，N95口罩共1200个，其中N95口罩不超过200个，钱恰好全部用完，则有几种购买方案，请列方程计算．

查看试题解析
24. 小红用110根长短相同的小木棍按照如图所示的方式，连续摆正方形或六边形，要求相邻的图形只有一条公共边.

(1)、小红首先用 $m$ 根小木棍摆出了 $p$ 个小正方形，请你用等式表示 $m ， p$ 之间的关系：；

(2)、小红用剩下的小木棍摆出了一些六边形，且没有木棍剩余.已知他摆出的正方形比六边形多4个，请你求出摆放的正方形和六边形各多少个?

(3)、小红重新用50根小木棍，摆出了 $s$ 排，共 $t$ 个小正方形.其中每排至少含有1个小正方形，每排含有的小正方形的个数可以不同.请你用等式表示 $s ， t$ 之间的关系，并写出所有 $s ， t$ 可能的取值.

查看试题解析
25. 雅安地震发生后，全国人民抗震救灾，众志成城，在地震发生一周年之际，某地政府又筹集了重建家园的必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）
车型
甲
乙
丙
汽车运载量（吨/辆）
5
8
10
汽车运费（元/辆）
400
500
600

(1)、全部物资可用甲型车8辆，乙型车5辆，丙型车辆来运送．

(2)、若全部物资都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？

(3)、为了节省运费，该地政府打算用甲、乙、丙三种车型同时参与运送，已知它们的总辆数为14辆，你能分别求出三种车型的辆数吗？此时的运费又是多少元？

查看试题解析
26. 阅读探索
（1）知识累计
解方程组 $\{\begin{matrix} (a - 1) + 2 (b + 2) = 6 \\ 2 (a - 1) + (b + 2) = 6 \end{matrix}$
解：设a﹣1=x，b+2=y，原方程组可变为 $\{\begin{matrix} x + 2 y = 6 \\ 2 x + y = 6 \end{matrix}$
解方程组得： $\{\begin{matrix} x = 2 \\ y = 2 \end{matrix}$ 即 $\{\begin{matrix} a - 1 = 2 \\ b + 2 = 2 \end{matrix}$
所以 $\{\begin{matrix} a = 3 \\ b = 0 \end{matrix}$
此种解方程组的方法叫换元法．
（2）拓展提高
运用上述方法解下列方程组： $\{\begin{matrix} (\frac{a}{3} - 1) + 2 (\frac{b}{5} + 2) = 4 \\ 2 (\frac{a}{3} - 1) + (\frac{b}{5} + 2) = 5 \end{matrix}$
（3）能力运用
已知关于x，y的方程组 $\{\begin{matrix} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{matrix}$ 的解为 $\{\begin{matrix} x = 5 \\ y = 3 \end{matrix}$ ，直接写出关于m、n的方程组 $\{\begin{matrix} 5 a_{1} (m + 3) + 3 b_{1} (n - 2) = c_{1} \\ 5 a_{2} (m + 3) + 3 b_{2} (n - 2) = c_{2} \end{matrix}$ 的解为．

查看试题解析

人数 $m$	0＜ $m$ ≤100	100＜ $m$ ≤200	$m$ ＞200
收费标准(元／人)	90	85	75

车型	甲	乙	丙
汽车运载量（吨/辆）	5	8	10
汽车运费（元/辆）	400	500	600

初中数学湘教版七年级下册第一章 二元一次方程组 单元测试（提高练）

一、单选题

二、填空题

三、解答题

初中数学湘教版七年级下册第一章二元一次方程组单元测试（提高练）