初中数学湘教版七年级下册1.3二元一次方程组的应用同步训练（提高篇）

试卷更新日期：2021-03-07 类型：同步测试

进入出卷网下载

一、单选题

1. 某小区准备新建 50 个停车位，已知新建 1 个地上停车位和 1 个地下停车位共需 0.6万元；新建 3 个地上停车位和 2 个地下停车位共需 1.3 万元，求该小区新建 1 个地上停车位和1个地下停车位各需多少万元？设新建1个地上停车位需要 x 万元，新建 1 个地下停车位需 y 万元，列二元一次方程组得（）

A、 ${\begin{array}{l} x + y = 6 \\ 3 x + 2 y = 1.3 \end{array}$ B、 ${\begin{array}{l} x + y = 6 \\ 2 x + 3 y = 1.3 \end{array}$ C、 ${\begin{array}{l} x + y = 0.6 \\ 3 x + 2 y = 1.3 \end{array}$ D、 ${\begin{array}{l} x + y = 6 \\ 3 x + 2 y = 13 \end{array}$

查看试题解析
2. “某工厂用如图甲所示的长方形和正方形纸板做成如图乙所示的 A、B 两种长方体形状的无盖纸盒.现有正方形纸板 120 张，长方形纸板 360 张，刚好全部用完，问能做成多少个 A 型盒子？”则下列结论正确的个数是（）

①甲同学：设 A 型盒子个数为 x 个，根据题意可得： 4x + 3 × $\frac{120 - x}{2}$ = 360②乙同学：设 B 型盒中正方形纸板的个数为 m 个，根据题意可得： 3 × $\frac{m}{2}$ + 4(120 - m) = 360③A 型盒 72 个④B 型盒中正方形纸板 48 个

A、1 B、2 C、3 D、4

查看试题解析
3. 如图，在长为30米，宽为20米的长方形花园里，原有两条面积相等的小路，其余部分绿化。现在为了增加绿地的面积，把公园里的一条小路改为绿地，只保留另一条小路，并且使得绿地面积是小路面积的4倍，则x与y的值为（）

A、 ${\begin{cases} x = 3 \\ y = 2 \end{cases}$ B、 ${\begin{cases} x = 5 \\ y = 4 \end{cases}$ C、 ${\begin{cases} x = 6 \\ y = 5 \end{cases}$ D、 ${\begin{cases} x = 6 \\ y = 4 \end{cases}$

查看试题解析
4. 《九章算术》是我国东汉初年编订的一部数学经典著作．在它的“方程”一章里，一次方程组是由算筹布置而成的．《九章算术》中的算筹图是竖排的，现在我们把它改为横排，如图1、图2．图中各行从左到右列出的算筹数分别表示未知数 $x$ ， $y$ 的系数与相应的常数项．把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来，就是 ${\begin{matrix} 2 x + 3 y = 27 ， \\ x + 2 y = 14. \end{matrix}$
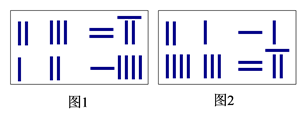
类似地，图2所示的算筹图我们可以表述为（）

A、 ${\begin{matrix} 2 x + y = 16 \\ 4 x + 3 y = 22 \end{matrix}$ B、 ${\begin{matrix} 2 x + y = 16 \\ 4 x + 3 y = 27 \end{matrix}$ C、 ${\begin{matrix} 2 x + y = 11 \\ 4 x + 3 y = 27 \end{matrix}$ D、 ${\begin{matrix} 2 x + y = 11 \\ 4 x + 3 y = 22 \end{matrix}$

查看试题解析
5. 一种饮料大小包装有3种，1个中瓶比2小瓶便宜2角，1个大瓶比1个中瓶加1个小瓶贵4角，大、中、小各买1瓶，需9元6角，若设小瓶单价为x角，大瓶为y角，可列方程为（）

A、 ${\begin{cases} 3 x + y = 98 \\ y - 3 x = 2 \end{cases}$ B、 ${\begin{cases} 3 x + y = 98 \\ y + 3 x = 2 \end{cases}$ C、 ${\begin{cases} 2 x + y = 98 \\ y - 3 x = 4 \end{cases}$ D、 ${\begin{cases} 3 x - y = 98 \\ 2 x + y = 4 \end{cases}$

查看试题解析

二、填空题

6. 如图，在两个形状、大小完全相同的大长方形内放入四个如图③的小长方形后得到如图①、②，已知大长方形的长为 $m$ ，则

(1)、若记小长方形的长为 $a$ ，宽为 $b (a > b)$ ，则 $a$ 和 $b$ 之间的数量关系是；

(2)、图①中阴影部分的周长与图②中阴影部分的周长的和是（结果用含 $m$ 的代数式表示）.

查看试题解析
7. 三位先生A，B，C带着他们的妻子a、b、c到超市购物，至于谁是谁的妻子现在只能从下列条件来推测：他们6人，每人花在买商品的钱数(单位：元)正好等于商品数量的平方，而且每位先生都比自己的妻子多花48元钱，又知先生A比b多买9件商品，先生B比a多买7件商品，则先生A的妻子是。

查看试题解析
8. 三位先生A、B、C带着他们的妻子a、b、c到超市购物，至于谁是谁的妻子现在只能从下列条件来推测：他们6人，每人花在买商品的钱数（单位：元）正好等于商品数量的平方，而且每位先生都比自己的妻子多花48元钱，又知先生A比b多买9件商品，先生B比a多买7件商品.则先生C购买的商品数量是.

查看试题解析
9. 三个同学对问题“若方程组 ${\begin{matrix} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{matrix}$ 的解是 ${\begin{matrix} x = 3 \\ y = 4 \end{matrix}$ ，求方程组 ${\begin{matrix} 3 a_{1} x + 2 b_{1} y = 5 c_{1} \\ 3 a_{2} x + 2 b_{2} y = 5 c_{2} \end{matrix}$ 的解．”提出各自的想法。甲说：“这个题目好像条件不够，不能求解”；乙说：“它们的系数有一定的规律，可以试试”；丙说：“能不能把第二个方程组的两个方程的两边都除以5，通过换元替换的方法来解决”．参考他们的讨论，你认为这个题目的解应该是．

查看试题解析
10. 如图，长方形ABCD中放入一个边长为10的的正方形AEFG，和两个边长都为5的正方形CHIJ及正方形DKMN. $S_{1}$ ， $S_{2}$ ， $S_{3}$ 表示对应阴影部分的面积，若 $3 S_{3} - S_{1} = 2 S_{2}$ ，且AD，AB的长为整数，则 $S_{2}$ 的值是．

查看试题解析

三、解答题

11. 武汉新冠肺炎疫情发生后，全国人民众志成诚抗疫救灾.某公司筹集了抗疫物资120吨打算运往武汉疫区，现有甲、乙、两三种车型供运输选择，每辆车的运载能力和运费如下表所示： (假设每辆车均满载)

车型

甲

乙

丙

运载量（吨/辆）

5

8

10

运费（元/辆）

450

600

700

(1)、全部物资一次性运送可用甲型车8辆，乙型车5辆，丙型车辆.

(2)、若全部物资仅用甲、乙两种车型一次性运完，需运费9600元，求甲、乙两种车型各需多少辆？

(3)、若该公司打算用甲、乙、丙三种车型同时参与运送，已知车辆总数为14辆，且一次性运完所有物资，你能分别求出三种车型的辆数吗？此时的总运费为多少元？

查看试题解析
12. 目前，新型冠状病毒在我国虽可控可防，但不可松懈.某校欲购置规格分别为 $300 m l$ 和 $500 m l$ 的甲、乙两种免洗手消毒液若干瓶.已知购买2瓶甲和1瓶乙免洗手消毒液需要55元，购买3瓶甲和4瓶乙免洗手消毒液需要145元.

(1)、求甲、乙两种免洗手消毒液的单价.

(2)、该校在校师生共1000人，平均每人每天都需使用10mL的免洗手消毒液，若校方采购甲、乙两种免洗手消毒液共花费5000元，则这批消毒液可使用多少天?

(3)、为节约成本，该校购买散装免洗手消毒液进行分装.现需将9.6L的免洗手消毒液全部装入最大容量分别为 $300 m l$ 和 $500 m l$ 的两种空瓶中(每瓶均装满)，若分装时平均每瓶需损耗 $20 m l$ ，请问如何分装能使总损耗最小，求出此时需要的两种空瓶的数量.

查看试题解析
13. 某治污公司决定购买10台污水处理设备.现有甲、乙两种型号的设备可供选择，其中每台的价格与月处理污水量如下表：

甲型

乙型

价格(万元/台)

x

y

处理污水量(吨/月)

300

260

经调查：购买一台甲型设备比购买一台乙型设备多2万元，购买3台甲型设备比购买4台乙型设备少2万元.

(1)、求x，y的值；

(2)、如果治污公司购买污水处理设备的资金不超过91万元，求该治污公司有哪几种购买方案；

(3)、在（2）的条件下，如果月处理污水量不低于2750吨，为了节约资金，请为该公司设计一种最省钱的购买方案.

查看试题解析

14. 某集团购买了150吨物资打算运往某地支援，现有甲、乙、丙三种车型供选择，每辆汽车的运载能力和运费如下表所示：（假设每辆车均满载）

车型	甲	乙	丙
汽车运载量（吨/辆）	5	8	10
汽车运费（元/辆）	1000	1200	1500

(1)、若全部物资都用甲、乙两种车型来运送，需运费24000元，问分别需甲、乙两种车型各多少辆？

(2)、若该集团决定用甲、乙、丙三种汽车共18辆同时参与运送，请你写出可能的运送方案，并帮助该集团找出运费最省的方案（甲、乙、丙三种车辆均要参与运送）.

查看试题解析

15. 第19届亚运会将于2022年在杭州举行，“丝绸细节”助力杭州打动世界.杭州丝绸公司为亚运会设计手工礼品，投入 $W$ 元钱，若以2条领带和1条丝巾为一份礼品，则刚好可制作600份礼品；若以1条领带和3条丝巾为一份礼品，则刚好可制作400份礼品.

(1)、若 $W = 24$ 万元，求领带及丝巾的制作成本是多少？

(2)、若用 $W$ 元钱全部用于制作领带，总共可以制作几条？

(3)、若用 $W$ 元钱恰好能制作300份其他的礼品，可以选择 $a$ 条领带和 $b$ 条丝巾作为一份礼品（两种都要有），请求出所有可能的 $a$ 、 $b$ 的值.

查看试题解析
16. 甲乙两地相距160千米，一辆汽车和一辆拖拉机同时由甲、乙两地相向而行，1小时20分相遇.相遇后，拖拉机继续前进，汽车在相遇处停留1个小时后调头按原速返回，汽车在返回后半个小时追上了拖拉机.

(1)、在这个问题中，1小时20分＝小时；

(2)、相向而行时，汽车行驶小时的路程+拖拉机行驶小时的路程＝160千米；同向而行时，汽车行驶小时的路程＝拖拉机行驶小时的路程；

(3)、全程汽车、拖拉机各自行驶了多少千米？

查看试题解析
17. 已知关于x，y的二元一次方程组 ${\begin{cases} x - y = 3 - a \\ x + 2 y = 5 a \end{cases}$ （a为实数）．

(1)、若方程组的解始终满足y=a+1，求a的值．

(2)、已知方程组的解也是方程bx+3y=1(b为实数，b≠0且b≠-6)的解．
①探究实数a，b满足的关系式．

②若a，b都是整数，求b的最大值和最小值．

查看试题解析

车型	甲	乙	丙
运载量（吨/辆）	5	8	10
运费（元/辆）	450	600	700

	甲型	乙型
价格(万元/台)	x	y
处理污水量(吨/月)	300	260

初中数学湘教版七年级下册1.3二元一次方程组的应用 同步训练（提高篇）

一、单选题

二、填空题

三、解答题

初中数学湘教版七年级下册1.3二元一次方程组的应用同步训练（提高篇）