初中数学华师大版九年级下学期 第27章测试卷
试卷更新日期:2021-03-06 类型:单元试卷
一、单选题
-
1. 已知M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下P点坐标不满足要求的是( )A、(3,5) B、(-3,5) C、(1,2) D、(1,-2)2. 如图,某大桥可以近似地看作半径为250m的圆中的一段圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为( )
 A、60m B、50m C、45m D、40m3. 如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于( )
A、60m B、50m C、45m D、40m3. 如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于( )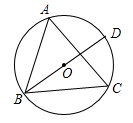 A、33° B、57° C、67° D、66°4. 如图, 是 的直径, 切 于点 , 交 于点 ;连接 ,若 ,则 等于( )
A、33° B、57° C、67° D、66°4. 如图, 是 的直径, 切 于点 , 交 于点 ;连接 ,若 ,则 等于( )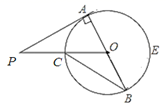 A、20° B、25° C、30° D、40°5. 如图,点A,B,C,D在⊙O上,AB=AC,∠A=40°,BD∥AC,若⊙O的半径为2.则图中阴影部分的面积是( )
A、20° B、25° C、30° D、40°5. 如图,点A,B,C,D在⊙O上,AB=AC,∠A=40°,BD∥AC,若⊙O的半径为2.则图中阴影部分的面积是( )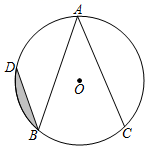 A、 ﹣ B、 ﹣ C、 ﹣ D、 ﹣6. 如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A,B,与⊙O1分别交于C,D,则 与 的弧长之和为( )
A、 ﹣ B、 ﹣ C、 ﹣ D、 ﹣6. 如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A,B,与⊙O1分别交于C,D,则 与 的弧长之和为( )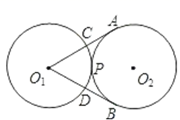 A、 B、 C、 D、7. 圆内接正六边形的边长与该边所对的劣弧的长的比是( )A、1: B、1:π C、3:π D、6:π
A、 B、 C、 D、7. 圆内接正六边形的边长与该边所对的劣弧的长的比是( )A、1: B、1:π C、3:π D、6:π二、填空题
-
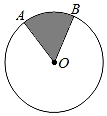
8. 一个直角三角形的两条直角边长分别为6cm、8cm,则它的内切圆的半径为cm.9. 如图,在半径为6的⊙O中,随意向圆内投掷一个小球,经过大量重复投掷后发现,小球落在阴影部分的概率稳定在 ,则 的长约为.(结果保留π)
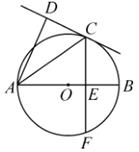
 10. 如图,AB是⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠BOE=54°,则∠C= .
10. 如图,AB是⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠BOE=54°,则∠C= .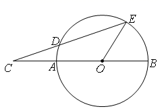 11. 如图, 内接于 , 于点D, ,若 的半径 ,则 的长为.
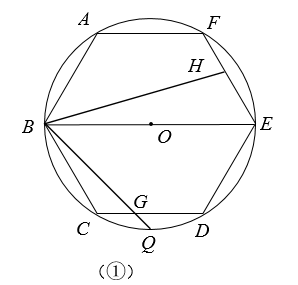
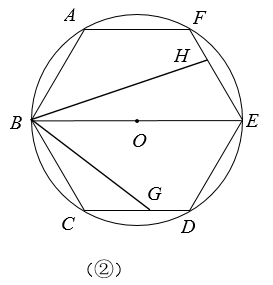
11. 如图, 内接于 , 于点D, ,若 的半径 ,则 的长为.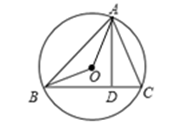 12. 如图,五边形 ABCDE 是⊙O 的内接正五边形, AF 是⊙O 的直径,则∠ BDF 的度数是°.
12. 如图,五边形 ABCDE 是⊙O 的内接正五边形, AF 是⊙O 的直径,则∠ BDF 的度数是°.
三、解答题
-
13. ⊙O的半径为5cm,弦AB=6cm,CD=8cm,且AB∥CD,求两弦之间的距离.14. 如图,AB是⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OB,CD的延长线交⊙O于点E.若∠C=19°,求∠BOE的度数.
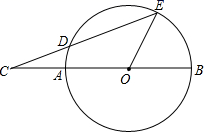 15. 如图, 的半径 , 于点C, .求 的长.
15. 如图, 的半径 , 于点C, .求 的长.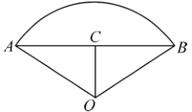
四、综合题
-
16. 如图, 中, ,P是斜边 上一个动点,以 为直径作 交 于点D,与 的另一个交点E,连接 .
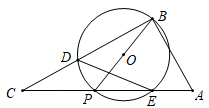 (1)、当 时,
(1)、当 时,①若 ,求 的度数;
②求证 ;
(2)、当 , 时,是否存在点P,使得 是等腰三角形,若存在,求出所有符合条件的 的长.