初中数学华师大版九年级下学期第27章 27.3 圆中的计算问题

试卷更新日期：2021-03-06 类型：同步测试

进入出卷网下载

1. 若扇形的半径为3，圆心角为60°，则此扇形的弧长是（）

A、π B、 2π C、 3π D、4π

查看试题解析
2. 如图，在由边长为1的小正方形组成的网格中，点A，B，C，D都在格点上，点E在AB的延长线上，以A为圆心，AE为半径画弧，交AD的延长线于点F，且弧EF经过点C，则 $\overset{⌢}{E F}$ 的长为（）

A、 $\frac{\sqrt{5} π}{4}$ B、 $\frac{5 π}{4}$ C、 $\frac{\sqrt{5} π}{8}$ D、 $\frac{5 π}{8}$

查看试题解析
3. 已知圆锥的母线长为6，将其侧面沿着一条母线展开，所得扇形的圆心角为120°，则该扇形面积是（）.

A、4π B、8π C、12π D、16π

查看试题解析
4. 如图，一块含有30°角的直角三角形ABC，在水平桌面上绕点C按顺时针方向旋转到A'、B'、C的位置。若BC的长为7.5cm，那么顶点A从开始到结束所经过的路径长为（）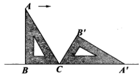

A、10πcm B、10 $\sqrt{3}$ πcm C、15πcm D、20π

查看试题解析
5. 如图，△ABC内接于☉O，若☉O的半径为6，∠A=60°，则 $\overset{⌢}{B C}$ 的长为（）

A、 $2 π$ B、 $4 π$ C、 $6 π$ D、 $8 π$

查看试题解析
6. 如图，在平行四边形 $A B C O$ 中， $∠ C = 45 °$ ，点 $A$ ， $B$ 在 $⊙ O$ 上，点 $D$ 在 $\overset{⌢}{A D B}$ 上， $D A = D B$ ，则 $∠ A O D$ 的度数为（）

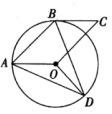A、112.5° B、120° C、135° D、150°

查看试题解析

7. 如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径r＝2，扇形的圆心角θ＝120°，则该圆锥母线l的长为.

查看试题解析
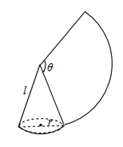8. 如图，一把折扇展开后的圆心角为120°，扇骨 $O A$ 长为 $30 cm$ ，扇面宽 $A B = 18 cm$ ，则该折扇的扇面的面积 $S =$ ${cm}^{2}$ .

查看试题解析
9. 如图，小明从纸上剪下一个圆形和一个扇形纸片，用它们恰好能围成一个圆锥模型.若圆的半径为1，扇形的圆心角为120°，则此扇形的半径为.

查看试题解析
10. 已知圆锥的底面半径为6，母线长为10，则此圆锥的侧面积为.

查看试题解析

11. 如图所示，在 Rt△ABC中，∠C=90°，AC=4 ，BC=3 .求以直角边所在直线为轴，把△ABC 旋转一周得到的圆锥的侧面积.

查看试题解析
12. 如图，点 $O$ 为 $R t △ A B C$ 斜边 $A B$ 上的一点，以 $O A$ 为半径的 $⊙ O$ 与 $B C$ 切于点 $D$ ，连接 $A D$ .

(1)、求证： $A D$ 平分 $∠ B A C$ ；

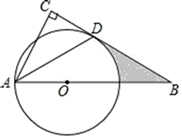(2)、若 $∠ B A C = 60 °$ ， $O A = 2 c m$ ，求阴影部分的面积（结果保留 $π$ ）

查看试题解析
13. 如图，AB是⊙O的直径，点C在⊙O上，∠CAB的平分线交⊙O于点D，过点D作AC的垂线交AC的延长线于点E.

(1)、证明：ED是⊙O的切线；

(2)、若⊙O半径为3，CE＝2，求BC的长.

查看试题解析
14. 如图所示， $△ A B C$ 内接于 $⊙ O ， ∠ A B C$ 的平分线交 $⊙ O$ 于D，连结 $A D ， C D$ .过B作 $⊙ O$ 的切线交 $A C$ 的延长线于E.

(1)、求证： $A D = C D$ .

(2)、若 $A C = 8 ， E C = 2$ ，求 $B E$ 的长.

(3)、若 $A B ， B C (A B > B C)$ 的长是一元二次方程 $x^{2} - 14 x + 48 = 0$ 的两根，若 $∠ A D C = 90^{°}$ ，直接写出 $A C$ 及 $B D$ 的长.

查看试题解析
15. 如图，已知AB为⊙O的直径，AC是⊙O的弦，D是弧BC的中点，过点D作⊙O的切线，分别交AC、AB的延长线于点E和点F，连接CD、BD．

(1)、求证：∠A＝2∠BDF；

(2)、若AC＝3，AB＝5，求CE的长．

查看试题解析

初中数学华师大版九年级下学期 第27章 27.3 圆中的计算问题