初中数学湘教版八年级下册1.2直角三角形的性质和判定(Ⅱ) 同步练习
试卷更新日期:2021-03-06 类型:同步测试
一、单选题
-
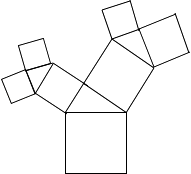
1. 一个直角三角形有两条边长分别为6和8,则它的第三条边长可能是( )A、8 B、9 C、10 D、112. 分别以下列五组数为一个三角形的边长:①6,8,10;②13,5,12 ③1,2,3;④9,40,41;⑤3 ,4,5 .其中能构成直角三角形的有( )组A、2 B、3 C、4 D、53. 在 ABC,如果AC2-AB2=BC2 , 那么( )A、 A= B、 B= C、 C= D、不能确定4. 甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )A、北偏西30° B、南偏西30° C、南偏东60° D、南偏西60°5. 一艘轮船以16海里/时的速度离开港口向东南方向航行,另一艘轮船在同时同地以12海里/时的速度向西南方向航行,它们离开港口3小时相距( )海里.A、60 B、30 C、20 D、806. 下列各组长度的线段能组成直角三角形的是( )A、a=2,b=3,c=4 B、a=4,b=4,c=5 C、a=5,b=6,c=7 D、a=5,b=12,c=137. 如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则所有正方形的面积的和是( )cm2 .
 A、28 B、49 C、98 D、1478. 下列几组数中,能作为直角三角形三边长度的是( )A、3,5,6 B、1,1, C、5,8,11 D、5,12,159. △ABC中,a=5,b=12,c=13.则S△ABC=( )A、60 B、30 C、78 D、10. 如图,正方形ABCD的边长为2,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S9的值为( )
A、28 B、49 C、98 D、1478. 下列几组数中,能作为直角三角形三边长度的是( )A、3,5,6 B、1,1, C、5,8,11 D、5,12,159. △ABC中,a=5,b=12,c=13.则S△ABC=( )A、60 B、30 C、78 D、10. 如图,正方形ABCD的边长为2,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S9的值为( )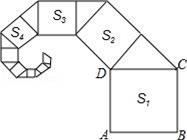 A、( )6 B、( )7 C、( )6 D、( )7
A、( )6 B、( )7 C、( )6 D、( )7二、填空题
-
11. 在△ABC中,∠B=90度,BC=6,AC=8,则AB=12. 在 中, , , ,斜边 的长为.13. 已知直角三角形三边长分别为3,4,m,则m=14. 已知一个直角三角形的两条直角边分别为6cm,8cm,那么这个直角三角形斜边上的高为 cm.
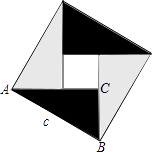
三、计算题
-
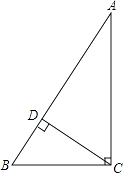
15. 已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.
四、解答题
-
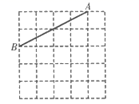
16. 如图,在正方形网格中,每个小正方形的顶点称为格点.画出以 为斜边的直角 ,且 的顶点均在格点上,各边长均为无理数.
 17. 计算图中四边形ABCD的面积.
17. 计算图中四边形ABCD的面积.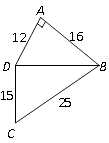 18. 如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号)
18. 如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号)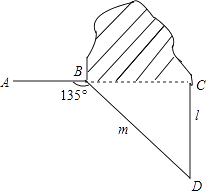
-