初中数学湘教版八年级下册1.1直角三角形的性质和判定（Ⅰ） 同步练习
试卷更新日期：2021-03-05 类型：同步测试
一、单选题
-
1. 如图，在△ABC中，∠C＝90°，点E是AC上的点，且∠1＝∠2，DE垂直平分AB，垂足是D，如果EC＝3cm，则AE等于（ ）
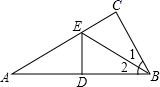A、3cm B、4cm C、6cm D、9cm2. 如图，在△ABC中，∠A＝45°，∠B＝30°，CD⊥AB于D，CD＝2，则AB长为( )
A、6 B、4 C、4 +2 D、2 +23. 一个直角三角形，两直角边长分别为3和4，下列说法正确的是（ ）A、斜边长为5 B、三角形的周长为25 C、斜边长为25 D、三角形的面积为204. 已知△ABC中，∠A＝20°，∠B＝70°，那么△ABC是（ ）A、直角三角形 B、锐角三角形 C、钝角三角形 D、正三角形5. 在一个直角三角形中，有一个锐角等于 ，则另一个锐角的度数是（ ）A、 B、 C、 D、6. 如图，在△ABC中，∠A=60°，BE⊥AC，垂足为E，CF⊥AB，垂足为F，点D是BC的中点，BE，CF交于点M，如果CM=4，FM=5，则BE等于（ ）
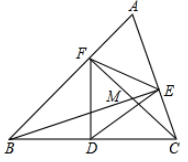A、14 B、13 C、12 D、117. 如图，已知在Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，F是BC边上的中点.若动点E从A点出发以2cm/s的速度沿着A→B→A方向运动，设运动时间为t(s)(0≤t＜3)，连结EF.当△BEF是直角三角形时，t的值为（ ）.
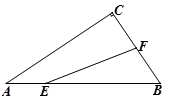A、 B、1 C、 或1或 D、 或1或8. 如图是某商场一楼与二楼之间的手扶电梯示意图．其中AB、CD分别表示一楼、二楼地面的水平线，∠ABC=150°，BC的长是8m，则乘电梯从点B到点C上升的高度h是（ ）
A、 m B、4m C、4 m D、8m9. △ABC中，∠A：∠B：∠C=1：2：3，最小边BC=4 cm，最长边AB的长是（ ）
A、5cm B、6cm C、7cm D、8cm10. 下列关于直角三角形的说法中错误的是（ ）A、直角三角形的两个锐角互余 B、直角三角形斜边的中点到三个顶点的距离相等 C、直角三角形斜边上的高等于斜边的一半 D、直角三角形中有两条边的平方和等于第三条边的平方二、填空题
-
11. 如果直角三角形的一个内角为40°，则这个直角三角形的另一个锐角为 ．12. 已知，如图，△ABC中，∠C=90°，∠A=30°，AB=6cm，则BC=cm.
13. 如图，矩形 ABCD 的对角线 AC 与 BD 相交于点 O，∠ADB＝30°，AB＝4，则 AD= ．
14. 等腰三角形腰上的高等于腰长的一半，则这个等腰三角形的顶角为度．三、解答题
-
15. 如图，在△ABC中，CE，BF是两条高，若∠A＝70°，∠BCE＝30°，求∠EBF与∠FBC的度数．
16. 如图，一艘轮船从点A向正北方向航行，每小时航行15海里，小岛P在轮船的北偏西15°，3小时后轮船航行到点B，小岛P此时在轮船的北偏西30°方向，在小岛P的周围20海里范围内有暗礁，如果轮船不改变方向继续向前航行，是否会有触礁危险？请说明理由。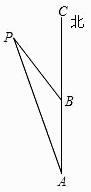
17.如图所示，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PC=4，求PD的长．
四、综合题
-
18. 清朝康熙皇帝是我国历史上对数学很有兴趣的帝王近日，西安发现了他的数学专著，其中有一文《积求勾股法》，它对“三边长为3、4、5的整数倍的直角三角形，已知面积求边长”这一问题提出了解法：“若所设者为积数（面积），以积率六除之，平方开之得数，再以勾股弦各率乘之，即得勾股弦之数”.用现在的数学语言表述是：“若直角三角形的三边长分别为3、4、5的整数倍，设其面积为S ， 则第一步： ＝m；第二步： ＝k；第三步：分别用3、4、5乘以k ， 得三边长”.(1)、当面积S等于150时，请用康熙的“积求勾股法”求出这个直角三角形的三边长；(2)、你能证明“积求勾股法”的符合题意性吗？请写出证明过程.19. 如图，已知∠ACB=90°，CD是AB上的高，∠A=30°，AB=4cm，则：
(1)、BC=；(2)、∠BCD=；(3)、BD=；(4)、AD= ．