初中数学华师大版九年级下学期 第26章 26.2 二次函数的图象与性质
试卷更新日期:2021-03-05 类型:同步测试
一、单选题
-
1. 二次函数y = ax2-2x-3(a<0)的图象一定不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知 时,二次函数 的图象如下列四个图之一所示.根据图象分析 的值等于( ).
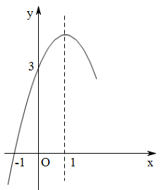
 A、-2 B、-1 C、1 D、23. 如图,抛物线 的对称轴为直线 ,与 轴的一个交点坐标为(-1,0),与 轴交点为(0,3),其部分图象如图所示,则下列结论错误的是( )
A、-2 B、-1 C、1 D、23. 如图,抛物线 的对称轴为直线 ,与 轴的一个交点坐标为(-1,0),与 轴交点为(0,3),其部分图象如图所示,则下列结论错误的是( )① ;②当 时, 随 的增大而减小;③当 时, ;④关于 的方程 有两个相等的实数根
 A、①③ B、②④ C、③④ D、①②④4. 将抛物线( )先向下平移1个单位长度,再向左平移2个单位长度后所得到的抛物线为 .A、 B、 C、 D、5. 已知函数 ,则( )A、当 时,y随x的增大而增大 B、当 时,y随x的增大而减小 C、当 时,y随x的增大而增大 D、当 时,y随x的增大而减小6. 对于二次函数 ,下列说法正确的是( )A、图象开口向下 B、图象和y轴交点的纵坐标为-3 C、 时,y随x的增大而减小 D、图象的对称轴是直线7. 把抛物线y=ax2+bx+c(a>0)作关于x轴的对称变换,所得图象的解析式为y=-a(x-1)2+4a , 若(m-1)a+b+c≤0,则m的最大值是( ).A、6 B、2 C、0 D、-48. 如图,a<0,b>0,c<0,那么二次函数y=ax2+bx+c的图像可能是( )A、
A、①③ B、②④ C、③④ D、①②④4. 将抛物线( )先向下平移1个单位长度,再向左平移2个单位长度后所得到的抛物线为 .A、 B、 C、 D、5. 已知函数 ,则( )A、当 时,y随x的增大而增大 B、当 时,y随x的增大而减小 C、当 时,y随x的增大而增大 D、当 时,y随x的增大而减小6. 对于二次函数 ,下列说法正确的是( )A、图象开口向下 B、图象和y轴交点的纵坐标为-3 C、 时,y随x的增大而减小 D、图象的对称轴是直线7. 把抛物线y=ax2+bx+c(a>0)作关于x轴的对称变换,所得图象的解析式为y=-a(x-1)2+4a , 若(m-1)a+b+c≤0,则m的最大值是( ).A、6 B、2 C、0 D、-48. 如图,a<0,b>0,c<0,那么二次函数y=ax2+bx+c的图像可能是( )A、 B、
B、 C、
C、 D、
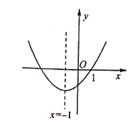
D、 9. 在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出以下结论:①abc <0;②c+2a<0;③9a-3b+c=0; ④a-b≥m(am+b) (m为实数):⑤4ac-b2<0。
9. 在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出以下结论:①abc <0;②c+2a<0;③9a-3b+c=0; ④a-b≥m(am+b) (m为实数):⑤4ac-b2<0。其中错误结论的个数有( )
 A、1个 B、2个 C、3个 D、4个10. 二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 与正比例函数y=cx在同一坐标系内的大致图象是( )
A、1个 B、2个 C、3个 D、4个10. 二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 与正比例函数y=cx在同一坐标系内的大致图象是( )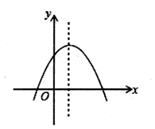 A、
A、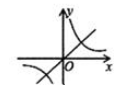 B、
B、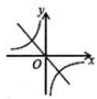 C、
C、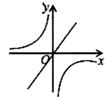 D、
D、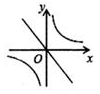
二、填空题
-
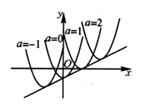
11. 已知点 P (x1 , y1 ), Q (x2 , y2)都在抛物线 y = x2-4x + 4上,若 x1 + x2 = 4,则y1 y2 .(填“>"、“<"或“=”)12. 在平面直角坐标系内抛物线y=x2﹣2x+3的图象先向左平移3个单位,再向上平移5个单位后图象对应的二次函数解析式为.13. 已知二次函数y=(x-2a)2+(a-1)(a为常数),当a取不同的值时,其图象构成一个“抛物线系”如图分别是当a=-1,a=0,a=1, a=2时二次函数的图象。它们的顶点在一条直线上, 这条直线的解析式是。
 14. 如图,平行四边形ABCD中, ,点 的坐标是 ,以点 为顶点的抛物线经过 轴上的点A , B , 则此抛物线的解析式为 .
14. 如图,平行四边形ABCD中, ,点 的坐标是 ,以点 为顶点的抛物线经过 轴上的点A , B , 则此抛物线的解析式为 .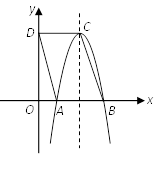
三、综合题
-
15. 若二次函数 的x与y的部分对应值如下表:
x
-1
0
1
2
3
4
y
0
3
4
3
0
-5
(1)、求这个二次函数的表达式;(2)、当x=﹣2时,y的值.16. 已知抛物线 y = x2 +bx + c 经过点(-1, 0), (3, 0).(1)、求该抛物线的对称轴.(2)、自变量x在什么范围内时,y随x的增大而减小?17. 已知抛物线y=a(x+4)2经过点M(﹣3,2),请解答下列问题:(1)、求抛物线的函数表达式,并说明此抛物线是由哪条抛物线经过平移得到的;(2)、求抛物线的开口方向,顶点坐标和对称轴;(3)、写出y随x的变化规律;(4)、求出函数的最大值或最小值.18. 已知二次函数图象的对称轴为y轴,且经过点(1,5)和(﹣ , ).(1)、求此二次函数的解析式;(2)、若将该二次函数先向下平移4个单位,再沿x轴翻折后与x轴交于A,B两点,设顶点为P,求△AOP的面积.
