山东省济宁市2020-2021学年高二上学期数学期末考试试卷
试卷更新日期:2021-03-04 类型:期末考试
一、单选题
-
1. 已知直线 与直线 平行,则实数a的值为( )A、 B、 C、6 D、-62. 圆 与圆 的位置关系为( )A、内含 B、外离 C、相交 D、相切3. 在等比数列 中, ,则 ( )A、4 B、8 C、16 D、324. 椭圆 与椭圆 的( )A、长轴长相等 B、短轴长相等 C、离心率相等 D、焦距相等5. 在空间四边形 中, ,且 ,则 ( )A、 B、 C、 D、6. 中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难次日脚痛减一半六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走了378里路,第一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”则此人第6天走了( )A、48里 B、24里 C、12里 D、6里7. 已知圆O的半径为5, ,过点P的2021条弦的长度组成一个等差数列 ,最短弦长为 ,最长弦长为 ,则其公差为( )A、 B、 C、 D、8. 已知抛物线 的焦点为F,点P为该抛物线上的动点,若 ,则当 最大时, ( )A、 B、1 C、 D、2
二、多选题
-
9. 已知空间四点 ,则下列说法正确的是( )A、 B、 C、点O到直线 的距离为 D、O,A,B,C四点共面10. 已知递减的等差数列 的前n项和为 ,若 ,则( )A、 B、当n=9时, 最大 C、 D、11. 已知圆 上至多有一点到直线 的距离为1,则实数m的取值可以是( )A、0 B、1 C、3 D、512. 已知常数 ,点 ,动点M(不与A,B重合)满足:直线 与直线 的斜率之积为 ,动点M的轨迹与点A,B共同构成曲线C,则关于曲线C的下列说法正确的是( )A、当 时,曲线C表示椭圆 B、当 时,曲线C表示焦点在y轴上的椭圆 C、当 时,曲线C表示双曲线,其渐近线方程为 D、当 且 时,曲线C的离心率是
三、填空题
-
13. 若 ,则数列 的前21项和 .14. 过点 作圆 的两条切线,切点为A,B,则直线 的一般式方程为.15. 在一平面直角坐标系中,已知 ,现沿x轴将坐标平面折成60°的二面角,则折叠后A,B两点间的距离为.16. 已知双曲线 的右焦点为F,以F为圆心,以a为半径的圆与双曲线C的一条渐近线交于A,B两点.若 (O为坐标原点),则双曲线C的离心率为.
四、解答题
-
17. 已知圆 ,直线 .(1)、若直线l平分圆C的周长,求实数k的值;(2)、若直线l与直线 的倾斜角互补,求圆C上的点到直线l的距离的最小值.18. 已知数列 的前n项和为 ,且 .(1)、求数列 的通项公式;(2)、设 , 为数列 的前n项和,求数列 的前n项和.19. 在① ;② 这两个条件中任选一个,补充在下面的问题中,并对其求解.
问题:已知抛物线 的焦点为F,点 在抛物线C上,且___________.
(1)、求抛物线C的标准方程;(2)、若直线l过抛物线C的焦点F,l与抛物线C相交于A,B两点,且 ,求直线l的方程.注:如果选择多个条件分别解答,按第一个解答计分.
20. 如图,在直四棱柱 中,四边形 为平行四边形, ,直线 与平面 所成角的正弦值为 .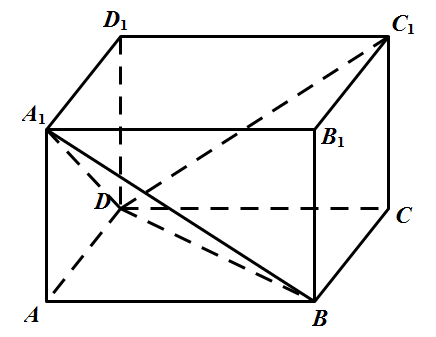 (1)、求点 到平面 的距离;(2)、求平面 与平面 的夹角的余弦值.
(1)、求点 到平面 的距离;(2)、求平面 与平面 的夹角的余弦值.