江西省新余市2020-2021学年度高二上学期理数期末考试试卷

试卷更新日期：2021-03-04 类型：期末考试

进入出卷网下载

一、单选题

1. 高二某班有学生52人，现将所有同学随机编号，用系统抽样的方法，抽取一个容量为4的样本，已知5号、31号、44号学生在样本中，则样本中还有一个学生的编号为（）

A、13 B、14 C、18 D、26

查看试题解析
2. 计算机执行下面的算法步骤后输出的结果是（）
$(1) a = 1 ； (2) b = 3 ； (3) a = a + b ； (4) b = a - b ； (5) 输出 a ， b .$

A、4，－2 B、4，1 C、4，3 D、6，0

查看试题解析
3. 从装有2个红球和2个黑球的口袋内任取两个球，那么互斥而不对立的事件是（）

A、至少有一个黑球与都是黑球 B、至少有一个黑球与至少有一个红球 C、恰好有一个黑球与恰好有两个黑球 D、至少有一个黑球与都是红球

查看试题解析
4. 在 $△ A B C$ 中，已知 $c = 2 a \cdot cos B$ ，那么 $△ A B C$ 一定是（）

A、等腰直角三角形 B、等腰三角形 C、直角三角形 D、等边三角形

查看试题解析
5. 执行如图所示的程序框图，若输出的结果为126，则判断框内的条件可以为（）

A、 $n \leq 5$ B、 $n \leq 6$ C、 $n \leq 7$ D、 $n \leq 8$

查看试题解析
6. 已知箱中装有4个白球和5个黑球，且规定：取出一个白球得2分，取出一个黑球得1分，现从该箱中任取（无放回，且每球取得的机会相等）3个球，则取出的3个球所得分数之和刚好为4的概率是（）

A、 $\frac{1}{21}$ B、 $\frac{2}{21}$ C、 $\frac{10}{21}$ D、 $\frac{5}{42}$

查看试题解析
7. 已知随机变量 $X$ 的分布列为：设 $Y = 2 X + 1$ ，则 $Y$ 的数学期望 $E (Y)$ 的值是（）

$X$

-1

0

1

$P$

$\frac{1}{2}$

$\frac{1}{6}$

$a$

A、 $- \frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $- \frac{2}{3}$

查看试题解析
8. 在 $Δ A B C$ 中，若 $\sqrt{3} \sin A + \cos A = 1$ ， $A B = 2$ ， $A C = 3$ ，则边 $B C$ 的长为（）

A、 $\sqrt{7}$ B、 $\sqrt{19}$ C、 $\sqrt{10}$ D、4

查看试题解析
9. 已知圆C的半径为2，在圆内随机取一点P，并以P为中点作弦AB，则弦长 $| A B | \leq 2 \sqrt{3}$ 的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{3}{4}$ C、 $\frac{2 - \sqrt{3}}{2}$ D、 $\frac{\sqrt{3}}{4}$

查看试题解析
10. 将两颗骰子各掷一次，设事件 $A =$ “两个点数都不相同”， $B =$ “至少出现一个5点”，则概率 $P (A | B) =$ （）

A、 $\frac{10}{11}$ B、 $\frac{5}{11}$ C、 $\frac{5}{18}$ D、 $\frac{5}{36}$

查看试题解析
11. 已知变量 $y$ 关于 $x$ 的回归方程为 $\hat{y} = e^{b x - 0.5}$ ，其一组数据如下表所示：

$x$

1

2

3

4

$y$

$e$

$e^{3}$

$e^{4}$

$e^{6}$

若 $x = 5$ ，则预测 $y$ 的值可能为（）

A、 $e^{5}$ B、 $e^{\frac{11}{2}}$ C、 $e^{7}$ D、 $e^{\frac{15}{2}}$

查看试题解析
12. 在体育选修课排球模块基本功 $($ 发球 $)$ 测试中，计分规则如下 $($ 满分为10分 $)$ ：①每人可发球7次，每成功一次记1分；②若连续两次发球成功加 $0.5$ 分，连续三次发球成功加1分，连续四次发球成功加 $1.5$ 分，以此类推， $\dots$ ，连续七次发球成功加3分 $.$ 假设某同学每次发球成功的概率为 $\frac{2}{3}$ ，且各次发球之间相互独立，则该同学在测试中恰好得5分的概率是（）

A、 $\frac{2^{6}}{3^{5}}$ B、 $\frac{2^{5}}{3^{5}}$ C、 $\frac{2^{6}}{3^{6}}$ D、 $\frac{2^{5}}{3^{6}}$

查看试题解析

二、填空题

13. 为了了解初中生的身体素质，某地区随机抽取了 $n$ 名学生进行跳绳测试，根据所得数据画样本的频率分布直方图如图所示，且从左到右第一小组的频数是100，则 $n =$ .

查看试题解析
14. 下列是某厂1~4月份用水量（单位：百吨）的一组数据，由其散点图可知，用水量 $y$ 与月份 $x$ 之间有较好的线性相关关系，其线性回归方程是 $\hat{y} = - 0.7 x + \hat{a}$ ，则 $\hat{a} =$ .

月份 $x$

1

2

3

4

用水量 $y$

4.5

4

3

2.5

查看试题解析
15. 若 ${(3 x + \sqrt{7})}^{4} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4}$ ，则 ${(a_{0} + a_{2} + a_{4})}^{2} - {(a_{1} + a_{3})}^{2}$ 的值为．

查看试题解析
16. 在区间[ $- 3 ， 5$ ]上随机取一个实数 $x$ ，则事件“ $1 \leq {(\frac{1}{2})}^{x} \leq 4$ ”发生的概率为．

查看试题解析

三、解答题

17. 在二项式 ${(\sqrt{x} - \frac{2}{x})}^{12}$ 的展开式中，

(1)、求展开式中含 $x^{3}$ 项的系数：

(2)、如果第 $3 k$ 项和第 $k + 2$ 项的二项式系数相等，试求 $k$ 的值.

查看试题解析
18. 在 $Δ A B C$ 中， $a$ ， $b$ ， $c$ 分别是角 $A$ ， $B$ ， $C$ 的对边，已知 $\frac{3 b - 2 a}{c} = \frac{2 \cos A - 3 \cos B}{\cos C}$ .

(1)、求 $\frac{\sin A}{\sin B}$ 的值；

(2)、若 $\cos C = - \frac{1}{4}$ ， $c = 8$ ，求 $Δ A B C$ 的面积.

查看试题解析
19. 某中学随机选取了40名男生，将他们的身高作为样本进行统计，得到如图所示的频率分布直方图．观察图中数据，完成下列问题．

（Ⅰ）求 $a$ 的值及样本中男生身高在 $[185 ， 195]$ （单位： $c m$ ）的人数；

（Ⅱ）假设同一组中的每个数据可用该组区间的中点值代替，通过样本估计该校全体男生的平均身高；

（Ⅲ）在样本中，从身高在 $[145 ， 155)$ 和 $[185 ， 195]$ （单位： $c m$ ）内的男生中任选两人，求这两人的身高都不低于 $185 c m$ 的概率．

查看试题解析
20. 如图，某测量人员为了测量西江北岸不能到达的两点 $A$ ， $B$ 之间的距离，她在西江南岸找到一点 $C$ ，从 $C$ 点可以观察到点 $A$ ， $B$ ；找到一个点 $D$ ，从 $D$ 点可以观察到点 $A$ ， $C$ ；找到一个点 $E$ ，从 $E$ 点可以观察到点 $B$ ， $C$ .测量得到数据： $∠ A C D = 90 °$ ， $∠ A D C = 60 °$ ， $∠ A C B = 15 °$ ， $∠ B C E = 105 °$ ， $∠ C E B = 45 °$ ， $D C = C E = 1$ .

(1)、求 $△ C D E$ 的面积；

(2)、求 $A$ ， $B$ 之间的距离.

查看试题解析

21. 某花圃为提高某品种花苗质量，开展技术创新活动，在A，B实验地分别用甲、乙方法培育该品种花苗．为观测其生长情况，分别在A，B试验地随机抽选各50株，对每株进行综合评分，将每株所得的综合评分制成如图所示的频率分布直方图．记综合评分为80及以上的花苗为优质花苗．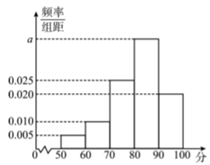

(1)、求图中a的值，并求综合评分的中位数；

(2)、用样本估计总体，以频率作为概率，若在A，B两块实验地随机抽取3棵花苗，求所抽取的花苗中的优质花苗数的分布列和数学期望；

(3)、填写下面的列联表，并判断是否有90%的把握认为优质花苗与培育方法有关．

	优质花苗	非优质花苗	合计
甲培育法	20
乙培育法		10
合计

附：下面的临界值表仅供参考．

P（K²≥k₀）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
$k_{0}$	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（参考公式： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ ．）

查看试题解析

22. 某县自启动精准扶贫工作以来，将伦晚脐橙种植作为帮助农民脱贫致富的主导产业.今年5月，伦晚脐橙喜获丰收.现从已采摘的伦晚中随机抽取1000个，测量这些果实的横径，得到如图所示的频率分布直方图．

(1)、已知这1000个伦晚脐橙横径的平均数 $\bar{x} = 72.5$ ，求这些伦晚脐橙横径方差 $s^{2}$ ．

(2)、根据频率分布直方图，可以认为全县丰收的伦晚横径值 $X$ 近似服从正态分布 $N (μ ， σ^{2})$ ，其中 $μ$ 近似为样本平均数 $\bar{x}$ ， $σ^{2}$ 近似为样本方差 $s^{2}$ ．
（ⅰ）若规定横径为 $66.4 ~ 84.7 mm$ 的为一级果，则从全县丰收的果实中任取一个，求恰好为一级果的概率；

（ⅱ）若规定横径为84.7mm以上的为特级果，现从全县丰收果实中任取一个进行进一步分析，如果取到的不是特级果，则继续抽取下一个，直到取到特级果为止，但抽取的总次数不超过 $n$ ，如果抽取次数 $ξ$ 的期望值不超过8，求 $n$ 的最大值．

（附： $\sqrt{35} = 5.9$ ， $\sqrt{37.5} = 6.1$ ， ${0.975}^{7} = 0.838$ ， ${0.975}^{8} = 0.817$ ， ${0.975}^{9} = 0.796$ ，

若 $X ~ N (μ ， σ^{2})$ ，则 $P (μ - σ < X < μ + σ) = 0.68$ ， $P (μ - 2 σ < X < μ + 2 σ) = 0.95$ ）

查看试题解析

$X$	-1	0	1
$P$	$\frac{1}{2}$	$\frac{1}{6}$	$a$

$x$	1	2	3	4
$y$	$e$	$e^{3}$	$e^{4}$	$e^{6}$

月份 $x$	1	2	3	4
用水量 $y$	4.5	4	3	2.5