浙江省绍兴市越城区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-04 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点(1,5)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 若a<b,则下列各式中一定成立的是()A、a+2>b+2 B、a-2>b-2 C、-2a>-2b D、 >3. 若一个三角形的两边长分别为3和7,则第三边长可能是( )A、6 B、3 C、2 D、114. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、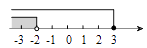 C、
C、 D、
D、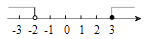 5.
5.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
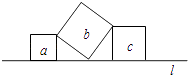 A、4 B、6 C、16 D、556. 点P1(x1 , y1),P2(x2 , y2),是一次函数y=5x+3图象上的两点,且y1<y2 , 则x1与x2的大小关系是( )A、x1>x2 B、x1=x2 C、x1<x2 D、不能确定7. 用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是( )
A、4 B、6 C、16 D、556. 点P1(x1 , y1),P2(x2 , y2),是一次函数y=5x+3图象上的两点,且y1<y2 , 则x1与x2的大小关系是( )A、x1>x2 B、x1=x2 C、x1<x2 D、不能确定7. 用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是( ) A、 B、 C、 D、8. 在平面直角坐标系中,已知 、 ,若要在x轴上找一点P,使 最短,则点P的坐标为( )A、 B、 C、 D、9. 如图,在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,点E、F、M、N是AD上的四点,则图中阴影部分的总面积是( )
A、 B、 C、 D、8. 在平面直角坐标系中,已知 、 ,若要在x轴上找一点P,使 最短,则点P的坐标为( )A、 B、 C、 D、9. 如图,在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,点E、F、M、N是AD上的四点,则图中阴影部分的总面积是( ) A、6 B、8 C、4 D、1210. 如图,∠AOB=45º,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若ΔPQR周长最小,则最小周长是( )
A、6 B、8 C、4 D、1210. 如图,∠AOB=45º,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若ΔPQR周长最小,则最小周长是( ) A、10 B、 C、20 D、
A、10 B、 C、20 D、二、填空题
-
11. 使代数式 有意义的x的取值范围是 .12. 把“同位角相等”写成“如果…那么…”的形式为:为 .13. 若方程组 的解x,y满足0<x+y<1,则k的取值范围是.14. 如图,等边△ABC的边长为2cm,D,E分别是AB,AC上的点,将△ADE沿直线DE折叠,点A落在点 处,且点 在△ABC外部,则阴影部分图形的周长为 cm
 15. 如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成 .设AB=x,若 为直角三角形,则x=.
15. 如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成 .设AB=x,若 为直角三角形,则x=. 16. 小王与小李约定下午3点在学校门口见面,为此,他们在早上8点将自己的手表对准,小王于下午3点到达学校门口,可是小李还没到,原来小李的手表比正确时间每小时慢4分钟.如果小李按他自己的手表在3点到达,则小王还需要等分钟(正确时间)
16. 小王与小李约定下午3点在学校门口见面,为此,他们在早上8点将自己的手表对准,小王于下午3点到达学校门口,可是小李还没到,原来小李的手表比正确时间每小时慢4分钟.如果小李按他自己的手表在3点到达,则小王还需要等分钟(正确时间)三、解答题
-
17.(1)、计算:(2)、解不等式组:18. 已知:A(0,1),B(2,0),C(4,3)
 (1)、在坐标系中描出各点,画出△ABC;(2)、求△ABC的面积;(3)、设点P在y轴上,且△APB与△ABC的面积相等,求P的坐标.19. 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:
(1)、在坐标系中描出各点,画出△ABC;(2)、求△ABC的面积;(3)、设点P在y轴上,且△APB与△ABC的面积相等,求P的坐标.19. 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证: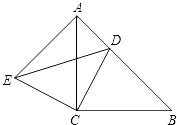 (1)、△ACE≌△BCD;(2)、AD2+DB2=DE2 .20. 某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
(1)、△ACE≌△BCD;(2)、AD2+DB2=DE2 .20. 某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)、若工厂计划获利14万元,问A,B两种产品应分别生产多少件?(2)、若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?(3)、在(2)的条件下,哪种生产方案获利最大?并求出最大利润.21. 如图,一次函数 的图象与正比例函数 的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D. (1)、求m的值.(2)、若一次函数图象经过点B(-2,-1),求一次函数的解析式.(3)、在(2)的条件下,求△AOD的面积.22. 已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE ,设∠BAD=α,∠CDE=β.
(1)、求m的值.(2)、若一次函数图象经过点B(-2,-1),求一次函数的解析式.(3)、在(2)的条件下,求△AOD的面积.22. 已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE ,设∠BAD=α,∠CDE=β. (1)、如图,若点D在线段BC上,点E在线段AC上.
(1)、如图,若点D在线段BC上,点E在线段AC上.①如果∠ABC=60°,∠ADE=70°, 那么α= , β=.
②求α、β之间的关系式.
(2)、是否存在不同于以上②中的α、β之间的关系式?若存在,求出这个关系式,若不存在,请说明理由.23. 模型建立: (1)、如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.
(1)、如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.求证:△BEC≌△CDA.
(2)、已知直线l1:y= x+4与y轴交于A点,将直线l1绕着A点顺时针旋转45°至l2 , 如图2,求l2的函数解析式.(3)、如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x-6上的一点,若△APD是不以A为直角顶点的等腰Rt△,请直接写出点D的坐标.