浙江省宁波市慈溪市2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-04 类型:期末考试
一、单选题
-
1. 下列四个数学符号中,是轴对称图形的是( )A、 B、 C、 D、2. 一个三角形的两边长分别是2与3,第三边的长不可能为( )A、2 B、3 C、4 D、53. 不等式x-2>0的解集在数轴上表示为( )
A、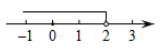 B、
B、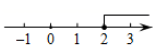 C、
C、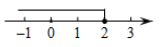 D、
D、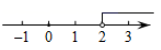 4. 下列计算正确的是( )A、 B、 C、 D、5. 能说明命题“对于任何实数 ”是假命题的一个反例可以是( )A、 B、 C、 D、6. 若 ,则下列各式正确的是( )A、 B、 C、 D、7. 若一次函数 ( 都是常数)的图象经过第一、二、四象限,则一次函数 的图象大致是( )A、
4. 下列计算正确的是( )A、 B、 C、 D、5. 能说明命题“对于任何实数 ”是假命题的一个反例可以是( )A、 B、 C、 D、6. 若 ,则下列各式正确的是( )A、 B、 C、 D、7. 若一次函数 ( 都是常数)的图象经过第一、二、四象限,则一次函数 的图象大致是( )A、 B、
B、 C、
C、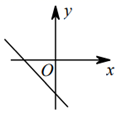 D、
D、 8. 已知 两地相距240千米.早上9点甲车从A地出发去B地,20分钟后,乙车从B地出发去A地.两车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示,则下列描述不正确的是( )
8. 已知 两地相距240千米.早上9点甲车从A地出发去B地,20分钟后,乙车从B地出发去A地.两车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示,则下列描述不正确的是( ) A、甲车的速度是60千米/小时 B、乙车的速度是90千米/小时 C、甲车与乙车在早上10点相遇 D、乙车在 到达A地9. 如图,以 为斜边的 和 位于直线 的同侧,连接 .若 ,则 的长为( )
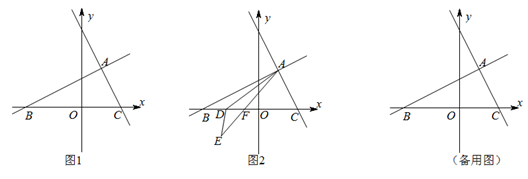
A、甲车的速度是60千米/小时 B、乙车的速度是90千米/小时 C、甲车与乙车在早上10点相遇 D、乙车在 到达A地9. 如图,以 为斜边的 和 位于直线 的同侧,连接 .若 ,则 的长为( ) A、3 B、4 C、 D、10. 如图,在平面直角坐标系中,O为坐标原点,直线 与x轴交于B点,与 轴交于A点,点 在线段 上,且 ,若点P在坐标轴上,则满足 的点P的个数是( )
A、3 B、4 C、 D、10. 如图,在平面直角坐标系中,O为坐标原点,直线 与x轴交于B点,与 轴交于A点,点 在线段 上,且 ,若点P在坐标轴上,则满足 的点P的个数是( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
11. 二次根式 中,x的取值范围是 .12. 把点 向左平移2个单位,所得点 的坐标为.13. 已知等腰三角形的一个内角为110°,则等腰三角形的底角的度数为.14. 如图,函数 和 的图象相交于点 ,则不等式 的解集为.
 15. 已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示,若DE=4,则DF=.
15. 已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示,若DE=4,则DF=.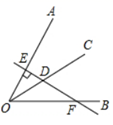 16. 如图所示,在等腰 中, ,点D为射线 上的动点, ,且 与 所在的直线交于点P,若 ,则 .
16. 如图所示,在等腰 中, ,点D为射线 上的动点, ,且 与 所在的直线交于点P,若 ,则 .
三、解答题
-
17.(1)、化简:(2)、解不等式:18. 如图,点C是线段 上一点, .
求证: .
 19. 如图,在 中,点D在边 的延长线上.完成下面的尺规作图(保留作图痕迹,不写作法):
19. 如图,在 中,点D在边 的延长线上.完成下面的尺规作图(保留作图痕迹,不写作法):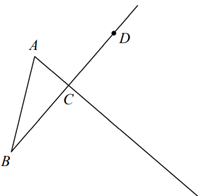 (1)、作边 的中点M.(2)、作 ,且点E在线段 的延长线上.20. 在平面直角坐标系中,O为坐标原点,点 位于第二象限,点 位于第三象限,且a为整数.(1)、求点A和点B的坐标.(2)、若点 为x轴上一点,且 是以 为底的等腰三角形,求m的值.21. 已知 与x成正比例,且当 时, .(1)、求y关于x的函数表达式.(2)、判断点 是否在函数的图象上,并说明理由.(3)、当 时,y的最小值为4,求m的值.22. 倡导垃圾分类,共享绿色生活.为了对回收的垃圾进行更精准的分类,某垃圾处理厂计划向机器人公司购买A型号和B型号垃圾分拣机器人共60台,其中B型号机器人不少于A型号机器人的1.4倍.(1)、该垃圾处理厂最多购买几台A型号机器人?(2)、机器人公司报价A型号机器人6万元/台,B型号机器人10万元/台,要使总费用不超过510万元,则共有几种购买方案?
(1)、作边 的中点M.(2)、作 ,且点E在线段 的延长线上.20. 在平面直角坐标系中,O为坐标原点,点 位于第二象限,点 位于第三象限,且a为整数.(1)、求点A和点B的坐标.(2)、若点 为x轴上一点,且 是以 为底的等腰三角形,求m的值.21. 已知 与x成正比例,且当 时, .(1)、求y关于x的函数表达式.(2)、判断点 是否在函数的图象上,并说明理由.(3)、当 时,y的最小值为4,求m的值.22. 倡导垃圾分类,共享绿色生活.为了对回收的垃圾进行更精准的分类,某垃圾处理厂计划向机器人公司购买A型号和B型号垃圾分拣机器人共60台,其中B型号机器人不少于A型号机器人的1.4倍.(1)、该垃圾处理厂最多购买几台A型号机器人?(2)、机器人公司报价A型号机器人6万元/台,B型号机器人10万元/台,要使总费用不超过510万元,则共有几种购买方案?