浙江省宁波市北仑区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-04 类型:期末考试
一、单选题
-
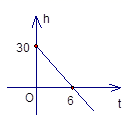
1. 在平面直角坐标系中,点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下面命题中,是假命题的为( )A、三角形的中线、角平分线、高都是线段 B、任意三角形的内角和都是 C、三角形的外角大于该三角形任意一个内角 D、直角三角形中的两个锐角互余3. 等腰三角形两边长分别为4和8,则这个等腰三角形的周长为( )A、16 B、18 C、20 D、16或204. 一根蜡烛长30cm,点燃后每小时燃烧5cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(小时)之间的函数关系用图像可以表示为中的( )A、
 B、
B、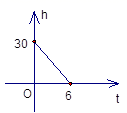 C、
C、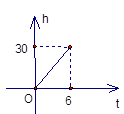 D、
D、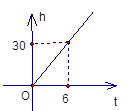 5. 若一次函数 的图象经过第二、三、四象限,则a的取值范围是( )A、a≠3 B、a>0 C、a<3 D、0<a<36. 如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠BAC=40°,则∠CHD的度数是( )
5. 若一次函数 的图象经过第二、三、四象限,则a的取值范围是( )A、a≠3 B、a>0 C、a<3 D、0<a<36. 如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠BAC=40°,则∠CHD的度数是( )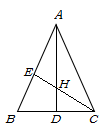 A、25° B、35° C、45° D、55°7. 将直线 向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为( )A、 B、 C、 D、8. 下图是2月26日至3月10日14天期间全国新冠肺炎新增确诊病例统计图,根据图中信息,下列描述不正确的是( )
A、25° B、35° C、45° D、55°7. 将直线 向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为( )A、 B、 C、 D、8. 下图是2月26日至3月10日14天期间全国新冠肺炎新增确诊病例统计图,根据图中信息,下列描述不正确的是( )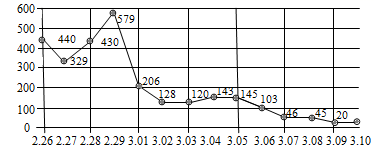 A、2月29日新增确诊病例数最多 B、3月1日新增确诊病例数较前日大幅下降 C、2月29日后新增确诊病例数持续下降 D、新增确诊病例数最少出现在3月9日9. 如图,一棵高5米的树 被强台风吹斜,与地面 形成 夹角,之后又被超强台风在点 处吹断,点 恰好落在 边上的点 处,若 ,则 的长是( )
A、2月29日新增确诊病例数最多 B、3月1日新增确诊病例数较前日大幅下降 C、2月29日后新增确诊病例数持续下降 D、新增确诊病例数最少出现在3月9日9. 如图,一棵高5米的树 被强台风吹斜,与地面 形成 夹角,之后又被超强台风在点 处吹断,点 恰好落在 边上的点 处,若 ,则 的长是( ) A、2 B、3 C、 D、10. 如图,平面直角坐标系中,一次函数 分别交 轴、 轴于 、 两点.若 是 轴上的动点,则 的最小值( )
A、2 B、3 C、 D、10. 如图,平面直角坐标系中,一次函数 分别交 轴、 轴于 、 两点.若 是 轴上的动点,则 的最小值( ) A、 B、6 C、 D、4
A、 B、6 C、 D、4二、填空题
-
11. 若 ,则 (填“>”或“<”).12. 已知点 A(2,m+3)与 B(n,﹣4)关于 x 轴对称,则 m+n=.13. 如图,在等腰 中, , ,则 边上的高是 .
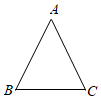 14. 不等式 的非负整数解共有个.15. 已知直线 与 轴交于 ,与 轴交于 ,若点 是坐标轴上的一点,且 ,则点 的坐标为.16. 在平面直角坐标系中,有直线 : 和直线 : ,直线 的有一个点 ,当 点到直线 的距离小于 ,则点 的横坐标取值范围是.
14. 不等式 的非负整数解共有个.15. 已知直线 与 轴交于 ,与 轴交于 ,若点 是坐标轴上的一点,且 ,则点 的坐标为.16. 在平面直角坐标系中,有直线 : 和直线 : ,直线 的有一个点 ,当 点到直线 的距离小于 ,则点 的横坐标取值范围是.三、解答题
-
17. 解不等式组 ,并把不等式组的解集在数轴上表示出来.
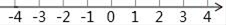 18. 已知:两边及其夹角,线段 , , .
18. 已知:两边及其夹角,线段 , , .求作: ,使 , ,(用尺规作图,保留作图痕迹,不写作法).
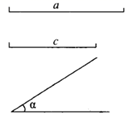
请你根据所学的知识,说明尺规作图作出 ,用到的是三角形全等判定定理中的_▲_,作出的 是唯一的,依据是三角形全等判定定理中的_▲_.
19. 某校组织学生开展了“2020新冠疫情”相关的手抄报竞赛.对于手抄报的主题,组织者提出了两条指导性建议:( 1 )A类“武汉加油”、B类“最美逆行者”、C类“万众一心抗击疫情”、D类“如何预防新型冠状病毒”4个中任选一个;
( 2 )E类为自拟其它与疫情相关的主题.
评奖之余,为了解学生的选题倾向,发掘出最能引发学生触动的主题素材,组织者随机抽取了部分作品进行了统计,并将统计结果绘制成了如下两幅尚不完整的统计图.
请根据以上信息回答:
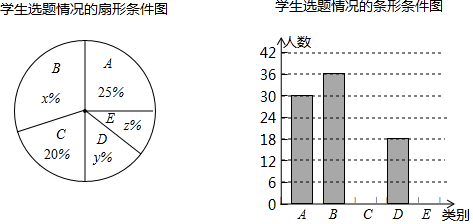 (1)、本次抽样调查的学生总人数是 , 并补全条形统计图;(2)、扇形统计图中,“C”对应的扇形圆心角的度数是 , x= , y﹣z=;(3)、本次抽样调查中,“学生手抄报选题”最为广泛的是类.(填字母)20. 平面直角坐标系中, 为原点,点 , , .
(1)、本次抽样调查的学生总人数是 , 并补全条形统计图;(2)、扇形统计图中,“C”对应的扇形圆心角的度数是 , x= , y﹣z=;(3)、本次抽样调查中,“学生手抄报选题”最为广泛的是类.(填字母)20. 平面直角坐标系中, 为原点,点 , , .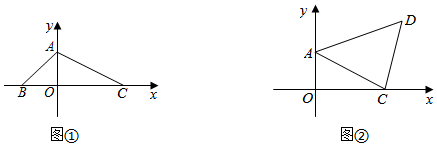 (1)、如图①,则三角形 的面积为;(2)、如图②,将点 向右平移7个单位长度,再向上平移4个单位长度,得到对应点 .
(1)、如图①,则三角形 的面积为;(2)、如图②,将点 向右平移7个单位长度,再向上平移4个单位长度,得到对应点 .①求 的面积;
②点 是一动点,若三角形 的面积等于三角形 的面积.请直接写出点 坐标.
21. 如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.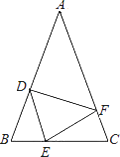 (1)、求证:△DEF是等腰三角形;(2)、当∠A=40°时,求∠DEF的度数;22. 某市组织20辆汽车装运食品、药品、生活用品三种救灾物资共100吨到灾区安置点,按计划20辆汽车都要装运,每辆汽车只能装运同一种救灾物资且必须装满,根据下表提供的信息,解答下列问题:
(1)、求证:△DEF是等腰三角形;(2)、当∠A=40°时,求∠DEF的度数;22. 某市组织20辆汽车装运食品、药品、生活用品三种救灾物资共100吨到灾区安置点,按计划20辆汽车都要装运,每辆汽车只能装运同一种救灾物资且必须装满,根据下表提供的信息,解答下列问题:物资种类
食品
药品
生活用品
每辆汽车运载量/吨
6
5
4
每吨所需运费/元
120
160
100
(1)、设装运食品的车辆数为x,装运药品的车辆数为y,求y与x的函数解析式;(2)、若装运食品的车辆数不少于5,装运药品的车辆数不少于6,则车辆的安排有几种方案?并写出每种安排方案;(3)、在(2)的条件下,若要求总运费最少,应采取哪种安排方案?并求出最少运费.23. 定义:如果一个三角形中有两个内角 , 满足 ,那我们称这个三角形为“近直角三角形”.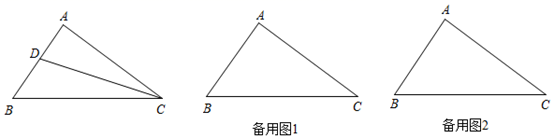 (1)、若 是“近直角三角形”, , ,则 度;(2)、如图,在 中, , , .若 是 的平分线,
(1)、若 是“近直角三角形”, , ,则 度;(2)、如图,在 中, , , .若 是 的平分线,①求证: 是“近直角三角形”;
②求 的长.
(3)、在(2)的基础上,边 上是否存在点 ,使得 也是“近直角三角形”?若存在,直接写出 的长;若不存在,请说明理由.24. 在平面直角坐标系中,已知点 , , , 是线段 上一点, 交 轴于 ,且 ,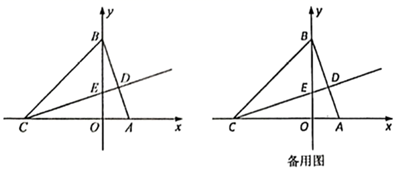 (1)、求直线 的解析式:(2)、求点 的坐标;(3)、猜想线段 与线段 的数量关系和位置关系,并说明理由;(4)、若 为射线 上一点,且 ,求点 的坐标.
(1)、求直线 的解析式:(2)、求点 的坐标;(3)、猜想线段 与线段 的数量关系和位置关系,并说明理由;(4)、若 为射线 上一点,且 ,求点 的坐标.