浙江省湖州市长兴县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-04 类型:期末考试
一、单选题
-
1. 下列图形中对称轴条数最多的是( )A、线段 B、正方形 C、圆 D、等边三角形2. 不等式 的解在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,已知 .能直接判断 的方法是( )
3. 如图,已知 .能直接判断 的方法是( ) A、 B、 C、 D、4. 直线 过点 ,则k的值是( )A、-2 B、-1 C、1 D、25. 对于命题“若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=2 B、a=﹣3,b=2 C、a=3,b=﹣1 D、a=﹣1,b=36. 三角形的一个外角是锐角,则此三角形的形状是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、无法确定7. 在平面直角坐标系中,三角形的三个顶点的横坐标保持不变,纵坐标都减去3,则所得图形可看成是将原图形( )A、向左平移3个单位 B、向右平移3个单位 C、向上平移3个单位 D、向下平移3个单位8. 如图,用尺规作 斜边 的垂直平分线,其中 ,现有以下结论:
A、 B、 C、 D、4. 直线 过点 ,则k的值是( )A、-2 B、-1 C、1 D、25. 对于命题“若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=2 B、a=﹣3,b=2 C、a=3,b=﹣1 D、a=﹣1,b=36. 三角形的一个外角是锐角,则此三角形的形状是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、无法确定7. 在平面直角坐标系中,三角形的三个顶点的横坐标保持不变,纵坐标都减去3,则所得图形可看成是将原图形( )A、向左平移3个单位 B、向右平移3个单位 C、向上平移3个单位 D、向下平移3个单位8. 如图,用尺规作 斜边 的垂直平分线,其中 ,现有以下结论:① ;② ;③ ;④ .其中正确的是( )
 A、①② B、①②③ C、①③④ D、①④9. 假期,小云带150元去图书馆,下表记录了他当天的所有支出,其中小零食支出的金额不小心被涂黑了,如果平均每包小零食的售价为5元,那么小云可能剩下的金额是( )
A、①② B、①②③ C、①③④ D、①④9. 假期,小云带150元去图书馆,下表记录了他当天的所有支出,其中小零食支出的金额不小心被涂黑了,如果平均每包小零食的售价为5元,那么小云可能剩下的金额是( )支出
午餐
购买课外资料
公交车票
小零食
金额(元)
15
120
4
A、1元 B、2元 C、3元 D、4元10. 如图,在 中, 于点D, 平分 交 于点E,交 于点F, , , ,则 的长是( ) A、3 B、4 C、5 D、
A、3 B、4 C、5 D、二、填空题
-
11. 已知三角形的三边长分别是2,x,5,则x的取值范围是.12. 如图, , , ,则 的度数是 .
 13. 已知一次函数 的图象经过 , 两点,则 (填“>”,“<”或“=”).14. 如图,在四边形ABCD中, , ,E是AC上的点,则图中共有对全等三角形.
13. 已知一次函数 的图象经过 , 两点,则 (填“>”,“<”或“=”).14. 如图,在四边形ABCD中, , ,E是AC上的点,则图中共有对全等三角形.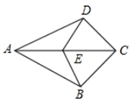 15. 如图,直线 经过 和 两点,则关于x的不等式组 的解是.
15. 如图,直线 经过 和 两点,则关于x的不等式组 的解是. 16. 如图,平面直角坐标系中,点A在直线 上,点C在直线 上,点A,C都在第一象限内,点B,D在x轴上,若 是等边三角形, 是以 为底边的等腰直角三角形,则点D的坐标为.
16. 如图,平面直角坐标系中,点A在直线 上,点C在直线 上,点A,C都在第一象限内,点B,D在x轴上,若 是等边三角形, 是以 为底边的等腰直角三角形,则点D的坐标为.
三、解答题
-
17.(1)、解不等式: ,并把它的解表示在数轴上.(2)、解不等式组:18. 如图,已知在平面直角坐标系中, 的三个顶点的坐标分别为 .
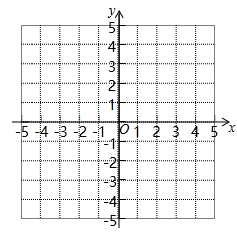
( 1 )画出 .
( 2 )若 与 关于x轴对称,点A,B,C的对应点分别是点D,E,F,画出 ,并写出点D,E,F的坐标.
19. 如图,已知在 中, ,D,E是 边上的两点,且 . (1)、求证: .(2)、若 ,且 , ,求 的面积.20. 在平面直角坐标系中,点 是一次函数 图象上一点.(1)、求m的值.(2)、当 时,求y的取值范围.21. 为了美化校园,某学校决定利用现有的332盆甲种花卉和310盆乙种花卉,搭配A,B两种园艺造型共50个,摆放在校园道路两侧.已知一个A种园艺造型需甲种花卉7盆,乙种花卉5盆;一个B种园艺造型需甲种花卉6盆,乙种花卉8盆.(1)、问搭配A,B两种园艺造型共有几种方案?(2)、若一个A种园艺造型的成本是200元,一个B种园艺造型的成本是300元,哪种方案成本最低?请写出此方案.22. 如图,平面直角坐标系中,直线 与直线 交于点B,与x轴交于点A.
(1)、求证: .(2)、若 ,且 , ,求 的面积.20. 在平面直角坐标系中,点 是一次函数 图象上一点.(1)、求m的值.(2)、当 时,求y的取值范围.21. 为了美化校园,某学校决定利用现有的332盆甲种花卉和310盆乙种花卉,搭配A,B两种园艺造型共50个,摆放在校园道路两侧.已知一个A种园艺造型需甲种花卉7盆,乙种花卉5盆;一个B种园艺造型需甲种花卉6盆,乙种花卉8盆.(1)、问搭配A,B两种园艺造型共有几种方案?(2)、若一个A种园艺造型的成本是200元,一个B种园艺造型的成本是300元,哪种方案成本最低?请写出此方案.22. 如图,平面直角坐标系中,直线 与直线 交于点B,与x轴交于点A. (1)、求点B的坐标.(2)、若点C在x轴上,且 是以 为腰的等腰三角形,求点C的坐标.23. 某数学活动小组在一次活动中,对一个数学问题作如下研究:
(1)、求点B的坐标.(2)、若点C在x轴上,且 是以 为腰的等腰三角形,求点C的坐标.23. 某数学活动小组在一次活动中,对一个数学问题作如下研究: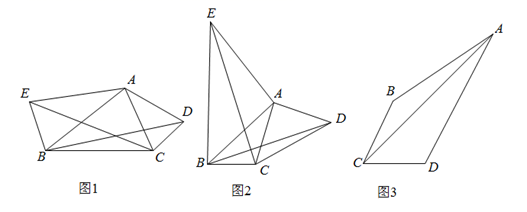 (1)、(问题呈现)
(1)、(问题呈现)如图1, 中分别以 为边向外作等腰 和等腰 ,使 , , ,连结 ,试猜想 与 的大小关系,并说明理由.
(2)、(问题再探)如图2, 中分别以 为边向外作等腰 和等腰 , ,连结 ,若 ,求 的长.
(3)、(问题拓展)如图3,四边形 中,连结 , , , , , ,请直接写出 的长.
24. 如图,已知在平面直角坐标系中,等腰 的边 在y轴的正半轴上,且 ,点C在第一象限,过点 的直线 经过点C. (1)、求点C的坐标及直线 的解析式.(2)、点E为直线 上的动点,若 的面积等于 面积的一半,求点E的坐标.(3)、点F为y轴上的动点,若 ,求点F的坐标.
(1)、求点C的坐标及直线 的解析式.(2)、点E为直线 上的动点,若 的面积等于 面积的一半,求点E的坐标.(3)、点F为y轴上的动点,若 ,求点F的坐标.