浙江省杭州市萧山区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-04 类型:期末考试
一、单选题
-
1. 点 在第一象限,则 的取值范围是( )A、 B、 C、 D、2. 不等式x≤2的解集在数轴上表示为( )A、
 B、
B、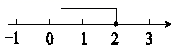 C、
C、 D、
D、 3. 若 ,则下列各式中一定成立的是( )A、 B、 C、 D、4. 有下列图形:①含 角的等腰三角形;②含 角的直角三角形;③含 角的直角三角形.其中是轴对称图形的有( )A、①②③ B、①② C、②③ D、①③5. 如图,在 中, , , 为中线,则 与 的周长之差为( )
3. 若 ,则下列各式中一定成立的是( )A、 B、 C、 D、4. 有下列图形:①含 角的等腰三角形;②含 角的直角三角形;③含 角的直角三角形.其中是轴对称图形的有( )A、①②③ B、①② C、②③ D、①③5. 如图,在 中, , , 为中线,则 与 的周长之差为( ) A、1 B、2 C、3 D、46. 已知直线y=-3x+b经过点A(1,y1)和点B(-2,y2),则y1与y2的大小关系是( )A、 B、 C、 D、不能确定7. 某游泳池水深 ,现需换水,每小时水位下降 ,那么剩下的高度 与时间 (小时)的关系图象表示为( )A、
A、1 B、2 C、3 D、46. 已知直线y=-3x+b经过点A(1,y1)和点B(-2,y2),则y1与y2的大小关系是( )A、 B、 C、 D、不能确定7. 某游泳池水深 ,现需换水,每小时水位下降 ,那么剩下的高度 与时间 (小时)的关系图象表示为( )A、 B、
B、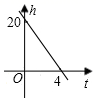 C、
C、 D、
D、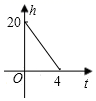 8. 在下列各组条件中,不能判断 和 全等的是( )A、 , , B、 , , C、 , , D、 , ,9. 已知等腰三角形 , ,点 是 上一点,若 , .则 的周长可能是( )A、15 B、20 C、28 D、3610. 小明和小华同时从小华家出发到球场去.小华先到并停留了8分钟,发现东西忘在了家里,于是沿原路以同样的速度回家去取.已知小明的速度为180米/分,他们各自距离小华家的路程 (米)与出发时间 (分)之间的函数关系如图所示,则下列说法正确的是( )
8. 在下列各组条件中,不能判断 和 全等的是( )A、 , , B、 , , C、 , , D、 , ,9. 已知等腰三角形 , ,点 是 上一点,若 , .则 的周长可能是( )A、15 B、20 C、28 D、3610. 小明和小华同时从小华家出发到球场去.小华先到并停留了8分钟,发现东西忘在了家里,于是沿原路以同样的速度回家去取.已知小明的速度为180米/分,他们各自距离小华家的路程 (米)与出发时间 (分)之间的函数关系如图所示,则下列说法正确的是( ) A、小明到达球场时小华离球场3150米 B、小华家距离球场3500米 C、小华到家时小明已经在球场待了8分钟 D、整个过程一共耗时30分钟
A、小明到达球场时小华离球场3150米 B、小华家距离球场3500米 C、小华到家时小明已经在球场待了8分钟 D、整个过程一共耗时30分钟二、填空题
-
11. 命题“等边三角形的三个内角都是60°”的逆命题是:.12. 若 地在 地的南偏东 方向,距离 地 处,则 地在 地的方向,距离 地 处.13. 若 是正比例函数,则 的取值范围是.14. 如图,在 中, 的中垂线 交 于点 ,交 于点 ,已知 , 的周长为22,则 .
 15. 若关于 的不等式组 .只有4个整数解,则 的取值范围是.16. 如图,在等腰 中, , , , 分别为 , 边上的点,将边 沿 折叠,使点 落在 上的点 处.当点 与点 重合时, .
15. 若关于 的不等式组 .只有4个整数解,则 的取值范围是.16. 如图,在等腰 中, , , , 分别为 , 边上的点,将边 沿 折叠,使点 落在 上的点 处.当点 与点 重合时, .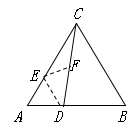
三、解答题
-
17. 解不等式: .18. 如图,在平面直角坐标系中,图形甲在第一象限.
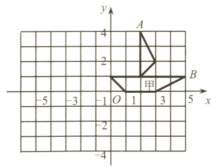
( 1 )请写出图形甲中点 和点 的坐标.
( 2 )作图形甲关于 轴对称的图形.
19. 如图,在 和 中, , ,若 , (1)、求证: .(2)、求 的度数.20. 已知一次函数 的图象经过点 和 .(1)、求该函数的表达式.(2)、若点 是 轴上一点,且 的面积为6,求点 的坐标.
(1)、求证: .(2)、求 的度数.20. 已知一次函数 的图象经过点 和 .(1)、求该函数的表达式.(2)、若点 是 轴上一点,且 的面积为6,求点 的坐标.


