浙江省杭州市下城区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期：2021-03-04 类型：期末考试
一、单选题
-
1. 以下列各组线段为边，能组成三角形的是（ ）A、1，2，3 B、1，3，5 C、2，3，4 D、2，6，102. 在平面直角坐标系中，点P(2，-4)位于（ ）．A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 要说明命题“若a>b，则a2>b2” 是假命题，可设（ ）A、a=3，b=4 B、a=4， b=3 C、a=－3，b=－4 D、a=－4，b=－34. 若x+2021>y+2021， 则（ ）A、x+2<y+2 B、x－2<y－2 C、2x<2y D、－2x<－2y5. 在Rt△ABC中，∠C=90°，点P在边AB上.BC=6， AC=8， （ ）A、若∠ACP=45°， 则CP=5 B、若∠ACP=∠B，则CP=5 C、若∠ACP=45°，则CP= D、若∠ACP=∠B，则CP=6. 把一个长为5，宽为2的长方形的长减少x (0≤x<5)， 宽不变，所得长方形的面积y关于x的函数表达式为（ ）A、y=10－x B、y=5x C、y=2x D、y=－2x+ 107. 若4≤x≤6，则（ ）A、2x－1>8 B、2x+1≥9 C、x+5≤9 D、3－x>－28. 用尺规作已知∠ABC的角平分线，步骤如下：①以B为圆心，以m为半径画弧，分别交射线BA， BC于点D， E； ②分别以D， E为圆心，以n为半径画弧，两弧在∠ABC内部交于点P；③画射线BP.射线BP即为所求.对m，n的描述，正确的是（ ）A、m>0， n>0 B、m>0，n<m C、m>0，n> DE D、m>0，n< DE9. 在△ABC中，∠BAC=90°，点D在边BC上，AD=AB （ ）
A、若AC=2AB，则∠C=30° B、若AC=2AB，则3BD=2CD C、若∠B=2∠C，则AC=2AB D、若∠B=2∠C，则S△ABD=2△ACD10. 甲，乙两车分别从A， B两地同时出发，相向而行.乙车出发2h后休息，当两车相遇时，两车立即按原速度继续向目的地行驶.设甲车行驶的时间为x(h)， 甲，乙两车到B地的距离分别为y1(km)， y2(km)， y1 ， y2关于x的函数图象如图.下列结论：①甲车的速度是 km/h；②乙车休息了0.5h；③两车相距a km时，甲车行驶了 h.正确的是（ ）
A、①② B、①③ C、②③ D、①②③二、填空题
-
11. “a 与2的和是非负数”用不等式表示为12. 设一次函数y=kx+3. 若当x=2时，y=－1，则k=13. 在等腰三角形ABC中，∠B=40°，若AB<BC，则∠C=14. 在△ABC中，∠A是钝角，∠B=30°， 设∠C的度数是α，则α的取值范围是15. 已知1<x<a，写一个符合条件的x (用含a的代数式表示)：16. 在△ABC中， AD是BC边上的高线，CE 是AB边上的中线，CD=AE，且CE<AC.若AD=6，AB=10，则CE=
三、解答题
-
17. 解关于x的不等式组：18. 如图，AC与BD相交于点O，AB//CD， OA=OC.
(1)、求证： △AOB≌△COD.(2)、若∠A+∠D=90°， AB=AC=2，求BD的长.19. 一次函数的图象过点A(－1， 2)和点B(1，－4)(1)、求该一次函数表达式.(2)、若点P(m－1， n1)和点Q(m+1， n2)在该一次函数的图象上，求n1－n2的值.20. 如图，在△ABC中， AB=AC.过点A作BC的平行线交∠ABC的角平分线于点D，连接CD.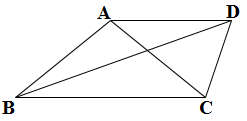
(1)、求证：△ACD为等腰三角形.(2)、若∠BAD=140°，求∠BDC的度数.21. 某水果店购买某种水果的进价为18元/千克，在销售过程中有10%的水果损耗，该水果店以a元/千克的标价出售该种水果.(1)、为避免亏本，求a的最小值.(2)、若该水果店以标价销售了70%的该种水果，在扣除10%损耗后，剩下的20%水果按10元/千克的价格售完.为确保销售该种水果所得的利润率不低于20%，求a的最小值.
