浙江省杭州市上城区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-04 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点 $P (3, 1)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 由下列长度的三条线段，能组成一个三角形的是（）

A、 $1, 2, 3$ B、 $3, 3, 6$ C、 $1, 5, 5$ D、 $4, 5, 10$

查看试题解析
3. 在平面直角坐标系中，点A（1，2）关于x轴对称的点的坐标是（）

A、（1，2） B、（1，－2） C、（－1，2） D、（－1，－2）

查看试题解析
4. 若 $x < y$ ，则 $m x > m y$ 成立的条件是（）

A、 $m \geq 0$ B、 $m \leq 0$ C、 $m > 0$ D、 $m < 0$

查看试题解析
5. 如图，在 $△ A B D$ 中， $∠ D = 80^{°}$ ，点 $C$ 为边 $B D$ 上一点，连结 $A C$ .若 $∠ A C B = 115^{°}$ ，则 $∠ C A D =$ （）

A、 $25^{°}$ B、 $35^{°}$ C、 $30^{°}$ D、 $45^{°}$

查看试题解析
6. 若等腰三角形的两边长分别是6和8，则它的周长是（）

A、20 B、22 C、20或22 D、18或20

查看试题解析
7. 下列命题为假命题的是（）

A、直角三角形斜边上的中线等于斜边的一半. B、两边及其一边的对角对应相等的两个三角形全等. C、等边三角形一边上的高线与这边上的中线互相重合. D、到线段两端点距离相等的点在这条线段的垂直平分线上.

查看试题解析
8. 一次函数 $y_{1} = - x + 7$ 与正比例函数 $y_{2} = \frac{4}{3} x$ ，若 $y_{1} < y_{2}$ 则自变量 $x$ 的取值范围是（）

A、 $x > 3$ B、 $x < 3$ C、 $x > 4$ D、 $x < 4$

查看试题解析
9. 若关于 $x$ 的不等式组 ${\begin{array}{l} x - 2 > 0 \\ 2 x - a + 1 < 0 \end{array}$ 有解，则一次函数 $y = (a - 3) x + 2$ 的图象一定不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
10. 如图，在 $Rt △ A B C$ 中， $C A = C B$ ， $D$ 为斜边 $A B$ 的中点， $Rt △ E D F$ 在 $△ A B C$ 内绕点 $D$ 转动，分别交边 $A C$ ， $B C$ 于点 $E$ ， $F$ （点 $E$ 不与点 $A$ ， $C$ 重合），下列说法正确的是（）
① $∠ D E F = 45^{°}$ ；② $B F^{2} + A E^{2} = E F^{2}$ ；③ $C D < E F \leq \sqrt{2} C D$

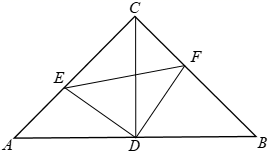A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题

11. 在平面直角坐标系中，将点 $A (3, 4)$ 向左平移3个单位后得到点的坐标为.

查看试题解析
12. 已知 $y$ 是关于 $x$ 的正比例函数，当 $x = - 1$ 时， $y = 2$ ，则 $y$ 关于 $x$ 的函数表达式为.

查看试题解析
13. 三角形的三边长分别为 $\sqrt{21}$ ，5，2，则该三角形最长边上的中线长为.

查看试题解析
14. 在平面直角坐标系中，线段 $A B$ 平行于 $x$ 轴，且 $A B = 4$ .若点 $A$ 的坐标为 $(- 1, 2)$ ，点 $B$ 的坐标为 $(a, b)$ ，则 $a + b =$ .

查看试题解析
15. 在平面直角坐标系中，直线 $y = x + 2$ 和直线 $y = - 2 x + b$ 的交点的横坐标为 $m$ .若 $- 1 \leq m < 3$ ，则实数 $b$ 的取值范围为.

查看试题解析
16. 在 $△ A B C$ 中， $∠ A B C = 90^{°}$ ， $C A = 3$ ， $C B = 1$ ， $D$ 为直线 $B C$ 上一点，且与 $△ A B C$ 的两个顶点构成等腰三角形，则此等腰三角形的面积为.

查看试题解析

三、解答题

17. 解不等式组：

(1)、 $5 x - 2 > 3 x + 1$ ；

(2)、 ${\begin{array}{l} 2 x + 3 > 2 (2 - x) \\ \frac{1 - x}{2} \geq \frac{2 x + 1}{3} - 1 \end{array}$ .

查看试题解析
18. 如图， $B D$ 为 $△ A B C$ 的角平分线， $E$ 为 $A B$ 上一点， $B E = B C$ ，连结 $D E$ .

(1)、求证： $△ B D C ≅ △ B D E$ ；

(2)、若 $A B = 7$ ， $C D = 2$ ， $∠ C = 90^{°}$ ，求 $△ A B D$ 的面积.

查看试题解析
19. 如图，线段 $a$ ，利用直尺和圆规按照下列要求作出图形.（保留作图痕迹，不要求写作法）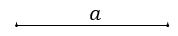

（ 1 ）作一个等边三角形，边长为 $a$ ；

（ 2 ）在第（1）题的图中，作一个 $∠ α$ ，使 $α = 30^{°}$ .

查看试题解析
20. 高空的气温与距地面的高度有关.已知某地的地面气温为24℃，该地距地面的高度每升高1km，气温下降6℃.

(1)、求距地面2km处的气温 $T$ ；

(2)、写出该地空中气温T（℃）与高度 $h (km)$ 之间的函数表达式；

(3)、若该地上空某处气温不低于0℃且不高于6℃，求此处距地面的高度 $h (km)$ 的范围.

查看试题解析
21. 如图，在 $△ A B C$ 中， $A D$ 是 $B C$ 边上的高线， $A D$ 的垂直平分线分别交 $A B$ ， $A C$ 于点 $E$ ， $F$ .

(1)、若 $∠ D A C = 30^{°}$ ，求 $∠ F D C$ 的度数；

(2)、试判断 $∠ B$ 与 $∠ A E D$ 的数量关系，并说明理由.

查看试题解析
22. 已知一次函数 $y_{1} = m x - 2 m + 4 (m \neq 0)$ .

(1)、判断点 $(2, 4)$ 是否在该一次函数的图象上，并说明理由；

(2)、若一次函数 $y_{2} = - x + 6$ ，当 $m > 0$ ，试比较函数值 $y_{1}$ 与 $y_{2}$ 的大小；

(3)、函数 $y_{1}$ 随 $x$ 的增大而减小，且与 $y$ 轴交于点 $A$ ，若点 $A$ 到坐标原点的距离小于 $6$ ，点 $B$ ， $C$ 的坐标分别为 $(0, - 2)$ ， $(2, 1)$ .求 $△ A B C$ 面积的取值范围.

查看试题解析
23. 如图，四边形 $A B C D$ ， $B C // A D$ ， $P$ 为 $C D$ 上一点， $P A$ 平分 $∠ B A D$ 且 $B P ⊥ A P$ .

(1)、若 $∠ B A D = 80^{°}$ ，求 $∠ A B P$ 的度数；

(2)、求证： $B A = B C + A D$ ；

(3)、设 $B P = 3 a$ ， $A P = 4 a$ ，过点 $P$ 作一条直线，分别与 $A D$ ， $B C$ 所在直线交于点 $E$ 点 $F$ .若 $A B = E F$ ，求 $A E$ 的长（用含 $a$ 的代数式表示）.

查看试题解析