初中数学苏科版九年级下册 第五章 二次函数 单元测试卷
试卷更新日期:2021-03-04 类型:单元试卷
一、单选题
-
1. 下列关系式中,属于二次函数的是( )A、 B、 C、 D、2. 抛物线y=3x2向左平移4个单位,再向下平移2个单位,所得到的抛物线是( )A、y=3(x﹣4)2+2 B、y=3(x﹣4)2﹣2 C、y=3(x+4)2﹣2 D、y=3(x+4)2+23. 抛物线y=x2–3x+5与坐标轴的交点个数为( )A、无交点 B、1个 C、2个 D、3个4. 若 是抛物线 上的三个点,则 、 、 的大小关系是( )A、 B、 C、 D、5. 直线y=bx+c与抛物线y=ax2+bx+c(a>0)在同一坐标系中大致图象可能是( )A、
 B、
B、 C、
C、 D、
D、 6. 已知二次函数 中,自变量x与函数y之间的部分对应值如表:
6. 已知二次函数 中,自变量x与函数y之间的部分对应值如表:x
0
1
2
3
y
2
3
2
在该函数的图象上有 和 两点,且 , , 与 的大小关系正确的是( )
A、 B、 C、 D、7. 一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( ) A、此抛物线的解析式是y=- x2+3.5 B、篮圈中心的坐标是(4,3.05) C、此抛物线的顶点坐标是(3.5,0) D、篮球出手时离地面的高度是2m8. 二次函数 图象上部分点的坐标 对应值列表如下:
A、此抛物线的解析式是y=- x2+3.5 B、篮圈中心的坐标是(4,3.05) C、此抛物线的顶点坐标是(3.5,0) D、篮球出手时离地面的高度是2m8. 二次函数 图象上部分点的坐标 对应值列表如下:x
…
0
1
2
3
…
y
…
-2
-3
-2
…
则下列说法错误的是( )
A、抛物线开口向上. B、抛物线的对称轴为直线 C、当 时, 随 的增大而增大 D、方程 有一个根小于9. 如图,二次函数 的图象与 轴交于两点 , ,其中 .下列四个结论:① ;② ;③ ;④ ,正确的个数是( ) A、1 B、2 C、3 D、410. 如图,在四边形 ABCD 中, AD∥BC , ∠A=45° , ∠C=90° , AD=4cm ,CD=3cm 、动点M,N同时从点A出发,点M以 cm/s 的速度沿 AB 向终点B运动,点N以2cm/s 的速度沿折线 AD-DC 向终点C运动.设点N的运动时间为ts ,△AMN 的面积为 Scm² ,则下列图象能大致反映S与t之间函数关系的是( )
A、1 B、2 C、3 D、410. 如图,在四边形 ABCD 中, AD∥BC , ∠A=45° , ∠C=90° , AD=4cm ,CD=3cm 、动点M,N同时从点A出发,点M以 cm/s 的速度沿 AB 向终点B运动,点N以2cm/s 的速度沿折线 AD-DC 向终点C运动.设点N的运动时间为ts ,△AMN 的面积为 Scm² ,则下列图象能大致反映S与t之间函数关系的是( )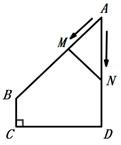 A、
A、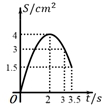 B、
B、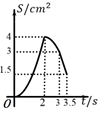 C、
C、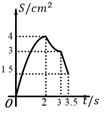 D、
D、
二、填空题
-
11. 抛物线y=3(x-2)2+3的顶点坐标是。12. 飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是 ,则经过s后,飞机停止滑行.13. 如图,抛物线 = 与直线 = 相交于点 , ,则关于 的方程 = 的解为 .
 14. 已知二次函数y=(x-2a)2+(a-1)(a为常数),当a取不同的值时,其图象构成一个“抛物线系”如图分别是当a=-1,a=0,a=1, a=2时二次函数的图象。它们的顶点在一条直线上, 这条直线的解析式是。
14. 已知二次函数y=(x-2a)2+(a-1)(a为常数),当a取不同的值时,其图象构成一个“抛物线系”如图分别是当a=-1,a=0,a=1, a=2时二次函数的图象。它们的顶点在一条直线上, 这条直线的解析式是。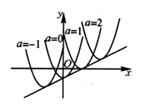 15. 如图,已知 的半径为2,圆心P在抛物线 上运动;当 与x轴相切时;圆心P的坐标为.
15. 如图,已知 的半径为2,圆心P在抛物线 上运动;当 与x轴相切时;圆心P的坐标为.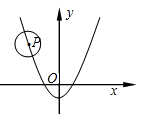 16. 如图,平行于x轴的直线AC分别交抛物线 y= x2(x≥0)与 (x≥0)于点B、C,过点C作y轴的平行线交y= x2于点D,直线DE∥AC,交 于点E,则 =.
16. 如图,平行于x轴的直线AC分别交抛物线 y= x2(x≥0)与 (x≥0)于点B、C,过点C作y轴的平行线交y= x2于点D,直线DE∥AC,交 于点E,则 =.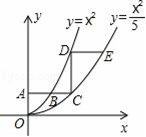 17. 已知函数y= ,且使y=k成立的x值恰好有2个,则k的取值范是 .18. 如图,在平面直角坐标系中,过点P(m,0)作x轴的垂线,分别交抛物线y=x2+ x+2和直线y= x-2于点A和点C,以线段AC为对角线作正方形ABCD,则当正方形ABCD的面积最小时m的值为。
17. 已知函数y= ,且使y=k成立的x值恰好有2个,则k的取值范是 .18. 如图,在平面直角坐标系中,过点P(m,0)作x轴的垂线,分别交抛物线y=x2+ x+2和直线y= x-2于点A和点C,以线段AC为对角线作正方形ABCD,则当正方形ABCD的面积最小时m的值为。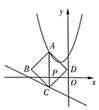
三、解答题
-
19. 已知抛物线的解析式为 ,求证:无论m取何值,抛物线与x轴总有两个交点.20. 在平面直角坐标系中,若抛物线 与直线 交于点 和点 ,其中 ,点 为原点,求 的面积.
 21. 已知二次函数y1=ax2+bx-3的图象经过点A(2,-3),B(-1,0),与y轴交于点C,与x轴另一交点交于点D.
21. 已知二次函数y1=ax2+bx-3的图象经过点A(2,-3),B(-1,0),与y轴交于点C,与x轴另一交点交于点D. (1)、求二次函数的解析式;(2)、求点C、点D的坐标;(3)、若一条直线y2 , 经过C、D两点,请直接写出y1>y2时,x的取值范围.22. 用一段长为28m的铁丝网与一面长为8m的墙面围成一个矩形菜园,为了使菜园面积尽可能的大,给出了甲、乙两种围法,请通过计算来说明这个菜园长、宽各为多少时,面积最大?最大面积是多少?
(1)、求二次函数的解析式;(2)、求点C、点D的坐标;(3)、若一条直线y2 , 经过C、D两点,请直接写出y1>y2时,x的取值范围.22. 用一段长为28m的铁丝网与一面长为8m的墙面围成一个矩形菜园,为了使菜园面积尽可能的大,给出了甲、乙两种围法,请通过计算来说明这个菜园长、宽各为多少时,面积最大?最大面积是多少?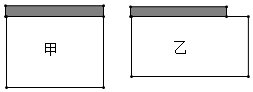 23. 体育测试时,九年级一名学生,双手扔实心球.已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处 点距离地面的高度为 ,当球运行的水平距离为 时,达到最大高度 的 处(如图),问该学生把实心球扔出多远?(结果保留根号)
23. 体育测试时,九年级一名学生,双手扔实心球.已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处 点距离地面的高度为 ,当球运行的水平距离为 时,达到最大高度 的 处(如图),问该学生把实心球扔出多远?(结果保留根号) 24. 如图所示,公园要造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面距离最大,高度2.25m.若不计其他因素,那么水池的半径至少要多少米才能使喷出的水流不致落到池外?
24. 如图所示,公园要造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面距离最大,高度2.25m.若不计其他因素,那么水池的半径至少要多少米才能使喷出的水流不致落到池外?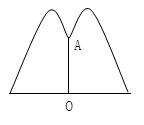 25. 在“美丽乡村”建设中,某村施工人员想利用如图所示的直角墙角,计划再用30米长的篱笆围成一个矩形花园 ,要求把位于图中点 处的一颗景观树圈在花园内,且景观树 与篱笆的距离不小2米.已知点 到墙体 、 的距离分别是8米、16米,如果 、 所在两面墙体均足够长,求符合要求的矩形花园面积 的最大值.
25. 在“美丽乡村”建设中,某村施工人员想利用如图所示的直角墙角,计划再用30米长的篱笆围成一个矩形花园 ,要求把位于图中点 处的一颗景观树圈在花园内,且景观树 与篱笆的距离不小2米.已知点 到墙体 、 的距离分别是8米、16米,如果 、 所在两面墙体均足够长,求符合要求的矩形花园面积 的最大值. 26. 某商店经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
26. 某商店经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:时间 x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)、求出y与x的函数关系式;(2)、问销售该商品第几天时,当天销售利润最大,最大利润是多少?(3)、在前50天销售过程中,为了给顾客发放福利,每售出一件商品就返还2a元给顾客,且要求售价不低于80元,但是前50天的销售中,仍可以获得最大利润5850元,求出a的值.27. 如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y= x2+bx+c经过点A、C,与AB交于点D.点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
 (1)、求抛物线的函数解析式.(2)、求S关于m的函数表达式.(3)、当S最大时,①求点Q的坐标.②若点F在抛物线y= x2+bx+c的对称轴上,且△DFQ的外心在DQ上,求点F的坐标.28. 如图,抛物线 与x轴交于点A,B,与y轴交于点 , .直线 交 于点D,点P是直线 下方抛物线上一动点,连接PD.
(1)、求抛物线的函数解析式.(2)、求S关于m的函数表达式.(3)、当S最大时,①求点Q的坐标.②若点F在抛物线y= x2+bx+c的对称轴上,且△DFQ的外心在DQ上,求点F的坐标.28. 如图,抛物线 与x轴交于点A,B,与y轴交于点 , .直线 交 于点D,点P是直线 下方抛物线上一动点,连接PD.
 (1)、求此抛物线的解析式;(2)、如图1,连接 ,求 面积的最大值及此时点P的坐标;(3)、如图2,连接 ,过点P作 于点E,是否存在点P使以P,D,E三点为顶点的三角形与 相似,若存在,直接写出点P的坐标;若不存在,请说明理由.
(1)、求此抛物线的解析式;(2)、如图1,连接 ,求 面积的最大值及此时点P的坐标;(3)、如图2,连接 ,过点P作 于点E,是否存在点P使以P,D,E三点为顶点的三角形与 相似,若存在,直接写出点P的坐标;若不存在,请说明理由.